| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俇俈 | 椷榓俇擭搙慜婜 | 丂嫗搒戝妛丂 | 丂棟宯 | 丒丒丒 | 丂妋棪丒嬌尷乮悢俙丒嘨乯 | 丂昗弨 |
嫗搒戝妛丂慜婜棟宯乮俀侽俀係乯
戞侾栤丂値屄偺堎側傞怓傪梡堄偡傞丅棫曽懱偺奺柺偵偄偢傟偐偺怓傪揾傞丅奺柺偵偳偺怓傪
丂揾傞偐偼摨條偵妋偐傜偟偄偲偡傞丅曈傪嫟桳偡傞偳偺擇偮偺柺偵傕堎側傞怓偑揾傜傟傞妋
丂棪 倫値 偲偡傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂倫4 傪媮傔傛丅
乮俀乯丂limn仺亣 倫値 傪媮傔傛丅
乮夝乯乮侾乯丂値亖係丂偺偲偒丄婲偙傝偆傞慡偰偺応崌偺悢偼丄丂係6亖係侽俋俇乮捠傝乯
丂乮忦審乯丂曈傪嫟桳偡傞偳偺擇偮偺柺偵傕堎側傞怓偑揾傜傟傞
偲偄偆忦審傪枮偨偡応崌偺悢傪媮傔傞丅
丂丂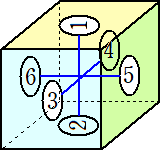
丂忋恾偺傛偆偵丄棫曽懱偺奺柺偵斣崋嘆丄嘇丄丒丒丒丄嘍丄嘐傪晅偗傞丅
嘆偲嘇偑摨怓偺偲偒丄揾傝曽偼丄係捠傝
丂偦偺偆偪偺侾捠傝偵懳偟偰丄嘊偺揾傝曽偼丄俁捠傝偱丄嘍偺揾傝曽偼丄俀捠傝
丂偦偺偆偪偺侾捠傝偵懳偟偰丄乮忦審乯傪枮偨偡嘋丄嘐偺揾傝曽傪峫偊傞丅
丂嘊偲嘋偑摨怓偺偲偒丄丂嘐偺揾傝曽偼丄俀捠傝
丂嘊偲嘋偑堎側傞怓偺偲偒丄嘐偺揾傝曽偼丄嘍偲摨偠怓偱丄侾捠傝
傛偭偰丄偙偺応崌偺悢偼丄丂係亊俁亊俀亊乮俀亄侾乯亖俈俀乮捠傝乯
嘆偲嘇偑堎側傞怓偺偲偒丄揾傝曽偼丄係亊俁亖侾俀乮捠傝乯
丂偦偺偆偪偺侾捠傝偵懳偟偰丄嘊偺揾傝曽偼丄俀捠傝偱丄嘍偺揾傝曽偼丄侾捠傝
丂傕偆巊偊傞怓偼側偄偺偱丄嘊偲嘋丄嘍偲嘐偼摨怓偲側傞丅
傛偭偰丄偙偺応崌偺悢偼丄丂侾俀亊俀亊侾亖俀係乮捠傝乯
埲忋偐傜丄媮傔傞応崌偺悢偼丄丂俈俀亄俀係亖俋俇乮捠傝乯丂側偺偱丄
丂妋棪 倫4亖俋俇/係侽俋俇亖俁/侾俀俉丂丂乮廔乯
乮俀乯丂値仺亣丂側偺偱丄値亞俇丂偲壖掕偟偰傛偄丅
丂曈傪嫟桳偡傞偳偺擇偮偺柺偵傕堎側傞怓偑揾傜傟傞妋棪偑 倫値 側偺偱丄
丂棫曽懱傪俇怓偱揾傝暘偗傟偽丄乮忦審乯傪昁偢枮偨偡偺偱丄偦偺曽朄偺悢偼丄
丂値乮値亅侾乯乮値亅俀乯乮値亅俁乯乮値亅係乯乮値亅俆乯丂捠傝
側偺偱丄丂値乮値亅侾乯乮値亅俀乯乮値亅俁乯乮値亅係乯乮値亅俆乯/値6亝倫値亝侾
偙偙偱丄丂嵍曈亖乮侾亅侾/値乯乮侾亅俀/値乯乮侾亅俁/値乯乮侾亅係/値乯乮侾亅俆/値乯仺侾丂乮値仺亣乯
側偺偱丄丂limn仺亣 倫値亖侾丂偱偁傞偙偲偑暘偐傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俁寧侾侽擔晅偗
丂丂
丂忋婰偱偼丄奺柺偺怓揾傝偵拝栚偟偰丄応崌偺悢傪悢偊偨偑丄巊偆怓悢偵拝栚偟偰丄応崌偺
悢傪悢偊傞偙偲傕弌棃傞丅
乮暿夝乯丂係怓偺偆偪俁怓梡偄傞応崌丂嘆亅嘇丄嘊亅嘋丄嘍亅嘐丂偑偦傟偧傟摨怓偱偁傟偽丄
乮忦審乯傪枮偨偡偺偱丄偙偺応崌偺悢偼丄丂4俠3丒俁亊俀亊侾亖俀係乮捠傝乯
丂係怓傪偡傋偰梡偄傞応崌偼丄嘆亅嘇丄嘊亅嘋丄嘍亅嘐丂偺偆偪侾慻偼堎側傞怓側偺偱丄
丂偙偺応崌偺悢偼丄丂3俠1丒係亊俁亊俀亊侾亖俈俀乮捠傝乯
丂埲忋偐傜丄乮忦審乯傪枮偨偡応崌偺悢偼丄丂俀係亄俈俀亖俋俇乮捠傝乯丂側偺偱丄
丂妋棪偼丄 倫4亖俋俇/係侽俋俇亖俁/侾俀俉丂偲側傞丅丂丂乮廔乯
丂偙偺暿夝偺媮傔曽偐傜丄乮俀乯偺 倫値 傪捈愙寁嶼偡傞偙偲偑壜擻偱偁傞丅
乮暿夝乯丂値怓偺偆偪丄俇怓傪梡偄傞応崌偺悢偼丄丂値俠6丒俇両亖値俹6乮捠傝乯
丂値怓偺偆偪丄俆怓傪梡偄傞応崌偼丄嘆亅嘇丄嘊亅嘋丄嘍亅嘐丂偺偆偪俀慻偼摨怓側偺偱丄
丂3俠2丒値俹5亖俁丒値俹5乮捠傝乯
丂値怓偺偆偪丄係怓傪梡偄傞応崌偼丄嘆亅嘇丄嘊亅嘋丄嘍亅嘐丂偺偆偪侾慻偼摨怓側偺偱丄
丂3俠1丒値俹4亖俁丒値俹4乮捠傝乯
丂値怓偺偆偪丄俁怓傪梡偄傞応崌偼丄嘆亅嘇丄嘊亅嘋丄嘍亅嘐丂偑偦傟偧傟摨怓側偺偱丄
丂n俠3丒俁亊俀亊侾亖値俹3乮捠傝乯
埲忋偐傜丄
丂倫値亖乮値俹6亄俁丒値俹5亄俁丒値俹4亄値俹3乯/値6
丂亖値乮値亅侾乯乮値亅俀乯乮乮値亅俁乯乮値亅係乯乮値亅俆乯亄俁乮値亅俁乯乮値亅係乯亄俁乮値亅俁乯亄侾乯/値6
丂亖値乮値亅侾乯乮値亅俀乯乮値3亅俋値2亄俀俋値亅俁俀乯/値6
丂亖乮侾亅侾/値乯乮侾亅俀/値乯乮侾亅俋/値亄俀俋/値2亅俁俀/値3乯
側偺偱丄丂limn仺亣 倫値亖侾丂偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂慜婜暥宯偱偼丄忋婰偺栤戣乮侾乯傪戞俀栤乮俀乯偲偟偰丄乽乮侾乯丂倫3 傪媮傔傛丅乿偲偄
丂丂偆椶戣偑弌戣偝傟偨丅
乮夝乯丂俁怓梡偄傞応崌丂嘆亅嘇丄嘊亅嘋丄嘍亅嘐丂偑偦傟偧傟摨怓側偺偱丄
乮忦審乯傪枮偨偡応崌偺悢偼丄丂俁亊俀亊侾亖俇乮捠傝乯
丂傛偭偰丄丂倫3亖俇/俁6亖俀/俀係俁丂丂乮廔乯
丂丂埲壓丄岺帠拞両丂