| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俇係 | 椷榓俆擭搙 | 丂杊塹堛壢戝妛丂 | 丂堛妛晹 | 丒丒丒 | 庬乆偺栤戣 | 丂昗弨 |
丂杊塹堛壢戝妛峑偺擖帋栤戣傗柾斖夝摎偼偁傑傝岞奐偝傟偰偄側偄丅偙偺儁乕僕偱偼丄栤戣
偲偦偺夝摎偵庢傝慻傒丄杊塹堛壢戝妛峑偺庴尡傪専摙偟偰偄傞庴尡惗偺堦彆偵側傟偽岾偄
偱偁傞丅
杊塹堛壢戝妛峑丂堛妛嫵堢晹乮俀侽俀俁乯
嘥丏丂倶倷 暯柺忋偵俀偮偺曻暔慄 俠1丗倷亖倶2丄俠2丗倷亖倶2亅倠2丂乮倠偼惓偺幚悢乯 偑偁傞丅
丂丂俠2忋偺揰俿偐傜俠1偵俀杮偺愙慄傪堷偒丄偦偺愙揰傪俙丄俛偲偡傞丅
丂丂乮俙偺 倶 嵗昗偼丄B偺 倶 嵗昗傛傝彫偝偄傕偺偲偡傞乯丅
丂丂丂偙偺偲偒丄埲壓偺栤偄偵摎偊傛丅
乮侾乯丂慄暘俙俛偺拞揰傪俵偲偟丄俿傪俠2忋偱摦偐偟偨偲偒偺俵偺婳愓偺曽掱幃俠3傪媮傔傛丅
乮俀乯丂俠3偑 俁倶2亄俀倶倷亅倷2亄俀倶亄俀倷亝侽 傪枮偨偡椞堟偵娷傑傟傞傛偆側 倠 偺抣偺斖埻傪
丂丂媮傔傛丅
乮夝乯乮侾乯丂俙乮兛丆兛2乯丄俛乮兝丆兝2乯丂乮兛亙兝乯丂丄俿乮倲丆倲2亅倠2乯丂偲偍偔偲丄
丂揰俙偵偍偗傞愙慄偺曽掱幃偼丄倷亖俀兛倶亅兛2丂側偺偱丄丂倲2亅倠2亖俀兛倲亅兛2
丂揰俛偵偍偗傞愙慄偺曽掱幃偼丄倷亖俀兝倶亅兝2丂側偺偱丄丂倲2亅倠2亖俀兝倲亅兝2
丂俀幃傪曈乆堷偄偰丄丂俀乮兛亅兝乯倲亅乮兛亅兝乯乮兛亄兝乯亖侽
丂兛亗兝丂側偺偱丄丂兛亄兝亖俀倲
丂俀幃傪曈乆懌偟偰丄丂俀乮倲2亅倠2乯亖俀乮兛亄兝乯倲亅乮兛2亄兝2乯亖係倲2亅乮兛2亄兝2乯
丂偡側傢偪丄丂兛2亄兝2亖俀倲2亄俀倠2
丂俵乮乮兛亄兝乯/俀丆乮兛2亄兝2乯/俀乯丂偵偍偄偰丄倶亖乮兛亄兝乯/俀丂丄倷亖乮兛2亄兝2乯/俀
偲偍偔偲丄兛亄兝亖俀倲丂傛傝丄丂倶亖倲丂丄兛2亄兝2亖俀倲2亄俀倠2丂傛傝丄丂倷亖倲2亄倠2
丂偟偨偑偭偰丄俠3偺曽掱幃偼丄丂倷亖倶2亄倠2
乮俀乯丂俁倶2亄俀倶倷亅倷2亄俀倶亄俀倷亖乮俁倶亅倷亄俀乯乮倶亄倷乯亝侽 傛傝丄壓恾偺椞堟傪摼傞丅
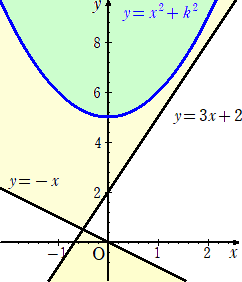 |
丂丂嵍恾傛傝丄戣堄傪枮偨偡偨傔偵偼丄俠3偑捈慄 丂 倷亖俁倶亄俀 偺忋曽乮愙偡傞応崌傕娷傓乯 丂偵偁傟偽傛偄丅 丂丂倶2亄倠2亞俁倶亄俀丂懄偪丄倶2亅俁倶亄倠2亅俀亞侽 丂敾暿幃傪俢偲偡傞偲丄丂俢亖俋亅係乮倠2亅俀乯亝侽 丂懄偪丄倠2亞侾俈/係丂偱丄俲亜侽傛傝丄丂倠亞 丂偑媮傔傞 倠 偺抣偺斖埻偱偁傞丅丂丂乮廔乯丂 |
嘦丏丂倢倧倗倎 倶乮倶亅俉乯亖俀丂丄倢倧倗倎 乮俆倶亅係俀乯亖侾丂傪摨帪偵枮偨偡幚悢 倶 偺抣傪 倶0 偲偟丄
丂丂偦偺偲偒偺 倎 偺抣傪 倎0 偲偍偔丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂倎0 偲 倶0 偺愊傪媮傔傛丅
乮俀乯丂倢倧倗倎 倶乮倶亅俉乯亖俀倢倧倗倎 乮俆倶亅係俀乯丂傪枮偨偡 倶 傪偡傋偰懌偟崌傢偣偨抣傪媮傔傛丅
乮夝乯乮侾乯丂恀悢忦審傛傝丄倶乮倶亅俉乯亜侽丂偐偮丂俆倶亅係俀亜侽丂偐傜丄丂倶亜係俀/俆
丂倢倧倗倎 倶乮倶亅俉乯亖俀倢倧倗倎 乮俆倶亅係俀乯丂側偺偱丄丂倶乮倶亅俉乯亖乮俆倶亅係俀乯2
揥奐偟偰惍棟偡傞偲丄丂俇倶2亅侾侽俁倶亄係係侾亖侽丂傛傝丄丂乮俇倶亅係俋乯乮倶亅俋乯亖侽
傛偭偰丄丂倶亖係俋/俇丂丄俋
丂偙偙偱丄倶亜係俀/俆丂側偺偱丄倶亖係俋/俇丂偼晄揔丅丂傛偭偰丄倶0亖俋
丂偙偺偲偒丄丂倢倧倗倎 俁亖侾丂偐傜丄丂倎0亖俁丂側偺偱丄丂倎0丒倶0亖俀俈
乮俀乯丂乮侾乯偐傜丄媮傔傞抣偼丄俋丂丂乮廔乯
嘨丏丂偡傋偰偺崁偑桳棟悢偱偁傞悢楍 乷倎値乸丄乷倐値乸偼埲壓偺傛偆偵掕媊偝傟傞傕偺偲偡傞丅
丂丂乮乮侾亄俆![]() 乯/侾侽乯値亖倎値亄
乯/侾侽乯値亖倎値亄![]() 倐値丂乮値亖侾丆俀丆俁丆丒丒丒乯
倐値丂乮値亖侾丆俀丆俁丆丒丒丒乯
丂偙偙偱丄倎値+1丄倐値+1 偼丄偦傟偧傟 倎値丄倐値 偲桳棟悢俙丄俛丄俠丄俢傪梡偄偰丄
丂丂倎値+1亖俙倎値亄俛倐値丂丄倐値+1亖俠倎値亄俢倐値
偲昞偡偙偲偑偱偒傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂俙亄俛亄俠亄俢丂偺抣傪媮傔傛丅
乮俀乯丂倢倝倣値仺亣儼倝=1値 倎倝 偺抣傪媮傔傛丅
乮夝乯乮侾乯丂乮乮侾亄俆![]() 乯/侾侽乯値+1
乯/侾侽乯値+1
丂丂亖乮乮侾亄俆![]() 乯/侾侽乯(倎値亄
乯/侾侽乯(倎値亄![]() 倐値)亖乮倎値亄侾俆倐値乯/侾侽亄
倐値)亖乮倎値亄侾俆倐値乯/侾侽亄![]() 乮俆倎値亄倐値乯/侾侽
乮俆倎値亄倐値乯/侾侽
丂傛傝丄倎値+1亖乮倎値亄侾俆倐値乯/侾侽丂丄倐値+1亖乮俆倎値亄倐値乯/侾侽丂側偺偱丄
丂俙亖侾/侾侽丂丄俛亖俁/俀丂丄俠亖侾/俀丂丄俢亖侾/侾侽
丂傛偭偰丄丂俙亄俛亄俠亄俢亖侾侾/俆
乮俀乯丂倎値+1亄![]() 倐値+1亖乮乮侾亄俆
倐値+1亖乮乮侾亄俆![]() 乯/侾侽乯乮倎値亄
乯/侾侽乯乮倎値亄![]() 倐値乯丂傛傝丄
倐値乯丂傛傝丄
丂丂倎値亄![]() 倐値亖乮倎1亄
倐値亖乮倎1亄![]() 倐1乯乮乮侾亄俆
倐1乯乮乮侾亄俆![]() 乯/侾侽乯n-1
乯/侾侽乯n-1
丂偙偙偱丄倎1亖侾/侾侽丂丄倐1亖侾/俀丂側偺偱丄丂倎1亄![]() 倐1亖乮侾亄俆
倐1亖乮侾亄俆![]() 乯/侾侽
乯/侾侽
丂傛偭偰丄丂倎値亄![]() 倐値亖乮乮侾亄俆
倐値亖乮乮侾亄俆![]() 乯/侾侽乯n
乯/侾侽乯n
丂傑偨丄倎値+1亅![]() 倐値+1亖乮倎値亄侾俆倐値乯/侾侽亅
倐値+1亖乮倎値亄侾俆倐値乯/侾侽亅![]() 乮俆倎値亄倐値乯/侾侽 傪惍棟偟偰丄
乮俆倎値亄倐値乯/侾侽 傪惍棟偟偰丄
丂倎値+1亅![]() 倐値+1亖乮乮侾亅俆
倐値+1亖乮乮侾亅俆![]() 乯/侾侽乯乮倎値亅
乯/侾侽乯乮倎値亅![]() 倐値乯丂偲側傞丅
倐値乯丂偲側傞丅
傛偭偰丄丂倎値亅![]() 倐値亖乮倎1亅
倐値亖乮倎1亅![]() 倐1乯乮乮侾亅俆
倐1乯乮乮侾亅俆![]() 乯/侾侽乯n-1亖乮乮侾亅俆
乯/侾侽乯n-1亖乮乮侾亅俆![]() 乯/侾侽乯n丂傛傝丄
乯/侾侽乯n丂傛傝丄
丂倎値亖乮侾/俀乯乮乮乮侾亄俆![]() 乯/侾侽乯n亄乮乮侾亅俆
乯/侾侽乯n亄乮乮侾亅俆![]() 乯/侾侽乯n乯
乯/侾侽乯n乯
丂 柍尷摍斾媺悢 倢倝倣値仺亣儼倝=1値 倎倝 偵偍偄偰丄
丂岞斾偵偮偄偰丄亅侾亙乮侾亅俆![]() 乯/侾侽亙乮侾亄俆
乯/侾侽亙乮侾亄俆![]() 乯/侾侽亙侾丂側偺偱丄廂懇偡傞丅
乯/侾侽亙侾丂側偺偱丄廂懇偡傞丅
傛偭偰丄倢倝倣値仺亣儼倝=1値 倎倝
亖乮侾/俀乯乮乮侾亄俆![]() 乯/侾侽乯/乮侾亅乮侾亄俆
乯/侾侽乯/乮侾亅乮侾亄俆![]() 乯/侾侽乯亄乮侾/俀乯乮乮侾亅俆
乯/侾侽乯亄乮侾/俀乯乮乮侾亅俆![]() 乯/侾侽乯/乮侾亅乮侾亅俆
乯/侾侽乯/乮侾亅乮侾亅俆![]() 乯/侾侽乯
乯/侾侽乯
亖乮侾/俀乯乮侾亄俆![]() 乯/乮俋亅俆
乯/乮俋亅俆![]() 乯亄乮侾/俀乯乮侾亅俆
乯亄乮侾/俀乯乮侾亅俆![]() 乯/乮俋亄俆
乯/乮俋亄俆![]() 乯
乯
亖乮乮侾亄俆![]() 乯乮俋亄俆
乯乮俋亄俆![]() 乯亄乮侾亅俆
乯亄乮侾亅俆![]() 乯乮俋亅俆
乯乮俋亅俆![]() 乯乯/侾俀
乯乯/侾俀
亖侾俇俉/侾俀亖侾係丂丂乮廔乯
嘩丏丂暋慺悢暯柺忋偵堎側傞俁揰俹1乮倸1乯丄俹2乮倸2乯丄俹3乮倸3乯偑偁傞丅暋慺悢 倸1丄倸2丄倸3 偑
丂丂師偺忦審傪枮偨偡偲偡傞丅
丂忦審侾丗丂倸12亄倸22亅倸1倸2亖侽
丂忦審俀丗丂乥倸1乥亖![]()
丂忦審俁丗丂倸3亖 倸1亄倸2
丂偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂乥倸2乥偺抣傪媮傔傛丅
乮俀乯丂仮倸1倸2倸3 偺柺愊傪媮傔傛丅
乮夝乯乮侾乯丂倸13亄倸23亖乮倸1亄倸2乯乮倸12亄倸22亅倸1倸2乯亖侽丂傛傝丄丂倸13亖亅倸23
丂傛偭偰丄乥倸1乥亖乥倸2乥側偺偱丄乥倸2乥亖![]()
乮俀乯丂倸12亄倸22亅倸1倸2亖侽丂傛傝丄乮倸1/z2乯2亅倸1/倸2亄侾亖侽丂傪夝偄偰丄
丂倸1/倸2亖乮侾亇![]() 乯/俀丂偐傜丄丂佢倸2俷倸1亖亇兾/俁丂乮俷偼尨揰乯
乯/俀丂偐傜丄丂佢倸2俷倸1亖亇兾/俁丂乮俷偼尨揰乯
丂傛偭偰丄仮俷倸1倸2 偼堦曈偺挿偝偑![]() 偺惓嶰妏宍偲側傞丅
偺惓嶰妏宍偲側傞丅
丂倸3亖 倸1亄倸2丂偐傜丄巐妏宍俷倸1倸3倸2偼暯峴巐曈宍偐偮傂偟宍偲側傞偺偱丄仮倸1倸2倸3 偼
丂堦曈偺挿偝偑![]() 偺惓嶰妏宍偲側傞丅
偺惓嶰妏宍偲側傞丅
丂傛偭偰丄丂仮倸1倸2倸3亖乮侾/俀乯![]() 2倱倝値乮兾/俁乯亖
2倱倝値乮兾/俁乯亖![]() /俀丂丂乮廔乯
/俀丂丂乮廔乯
嘪丏丂敀嬍俁屄丄崟嬍俇屄偺寁俋屄偺嬍慡偰傪俁偮偺敔俙丄俛丄俠偵暘偗傞偙偲傪峫偊傞丅暘偗
丂丂曽偺悢偊曽偵偮偄偰偼摨偠怓偺嬍偼嬫暿偣偢丄敔偼嬫暿偡傞傕偺偲偡傞丅傑偨丄嬍偑擖
丂丂傜側偄敔偑偁傞応崌傕暘偗曽偲偟偰悢偊傞傕偺偲偡傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂暘偗曽偺憤悢傪媮傔傛丅
乮俀乯丂偳偺敔偵傕彮側偔偲傕侾屄埲忋嬍偑擖傞暘偗曽偺悢傪媮傔傛丅
乮俁乯丂偳偺敔偵傕敀嬍偑俀屄埲忋傑偨偼崟嬍偑俀屄埲忋擖傞暘偗曽偺悢傪媮傔傛丅
乮夝乯乮侾乯敀俁屄傪俁偮偺敔俙丄俛丄俠偵暘偗傞曽朄偺悢偼丄
乮俙丆俛丆俠乯亖乮俁丆侽丆侽乯丄乮俀丆侾丆侽乯丄乮俀丆侽丆侾乯丄乮侾丆俀丆侽乯丄乮侾丆侾丆侾乯丄乮侾丆侽丆俀乯丄
丂丂乮侽丆俁丆侽乯丄乮侽丆俀丆侾乯丄乮侽丆侾丆俀乯丄乮侽丆侽丆俁乯丂偺侾侽捠傝
偙偺偆偪偺侾捠傝偵懳偟偰丄崟俇屄傪俁偮偺敔俙丄俛丄俠偵暘偗傞曽朄偺悢偼丄
乮俙丆俛丆俠乯亖乮俇丆侽丆侽乯丄乮俆丆侾丆侽乯丄乮俆丆侽丆侾乯丄乮係丆俀丆侽乯丄乮係丆侾丆侾乯丄乮係丆侽丆俀乯丄
丂丂乮俁丆俁丆侽乯丄乮俁丆俀丆侾乯丄乮俁丆侾丆俀乯丄乮俁丆侽丆俁乯丄乮俀丆係丆侽乯丄乮俀丆俁丆侾乯丄乮俀丆俀丆俀乯丄
丂丂乮俀丆侾丆俁乯丄乮俀丆侽丆係乯丄乮侾丆俆丆侽乯丄乮侾丆係丆侾乯丄乮侾丆俁丆俀乯丄乮侾丆俀丆俁乯丄乮侾丆侾丆係乯丄
丂丂乮侾丆侽丆俆乯丄乮侽丆俇丆侽乯丄乮侽丆俆丆侾乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄乮侽丆俀丆係乯丄乮侽丆侾丆俆乯丄
丂丂乮侽丆侽丆俇乯丂偺俀俉捠傝
丂傛偭偰丄暘偗曽偺憤悢偼丄丂侾侽亊俀俉亖俀俉侽乮捠傝乯
乮暿夝乯丂敀俁屄傪敔俙偵擖傟傞曽朄偼丄俁丄俀丄侾丄侽丂偺係捠傝
丂偦傟傜偵懳偟偰丄巆傝偺嬍傪敔俛丄俠偵擖傟傞曽朄偺悢偼丄侾丄俀丄俁丄係乮捠傝乯偺寁侾侽捠傝
丂崟俇屄傪敔俙偵擖傟傞曽朄偼丄俇丄俆丄係丄俁丄俀丄侾丄侽丂偺俈捠傝
丂偦傟傜偵懳偟偰丄巆傝偺嬍傪敔俛丄俠偵擖傟傞曽朄偺悢偼丄
丂侾丄俀丄俁丄係丄俆丄俇丄俈乮捠傝乯偺寁俀俉捠傝
丂傛偭偰丄暘偗曽偺憤悢偼丄丂侾侽亊俀俉亖俀俉侽乮捠傝乯
乮暿夝乯丂3俫3亊3俫6亖侾侽亊俀俉亖俀俉侽乮捠傝乯
乮俀乯丂俀偮偺敔偑嬻偵側傞応崌
丂敀乮俁丆侽丆侽乯偵懳偟偰丄崟乮俇丆侽丆侽乯
丂敀乮侽丆俁丆侽乯偵懳偟偰丄崟乮侽丆俇丆侽乯
丂敀乮侽丆侽丆俁乯偵懳偟偰丄崟乮侽丆侽丆俇乯
丂侾偮偺敔偑嬻偵側傞応崌
丂敀乮俁丆侽丆侽乯偵懳偟偰丄崟乮俆丆侾丆侽乯丄乮俆丆侽丆侾乯丄乮係丆俀丆侽乯丄乮係丆侽丆俀乯丄乮俁丆俁丆侽乯丄
丂丂乮俁丆侽丆俁乯丄乮俀丆係丆侽乯丄乮俀丆侽丆係乯丄乮侾丆俆丆侽乯丄乮侾丆侽丆俆乯丄乮侽丆俇丆侽乯丄乮侽丆侽丆俇乯
丂敀乮俀丆侾丆侽乯偵懳偟偰丄崟乮俇丆侽丆侽乯丄乮俆丆侾丆侽乯丄乮係丆俀丆侽乯丄乮俁丆俁丆侽乯丄乮俀丆係丆侽乯丄乮侾丆俆丆侽乯丄
丂丂乮侽丆俇丆侽乯
丂敀乮俀丆侽丆侾乯偵懳偟偰丄崟乮俇丆侽丆侽乯丄乮俆丆侽丆侾乯丄乮係丆侽丆俀乯丄乮俁丆侽丆俁乯丄乮俀丆侽丆係乯丄
丂丂乮侾丆侽丆俆乯丄乮侽丆侽丆俇乯
丂敀乮侾丆俀丆侽乯偵懳偟偰丄崟乮俇丆侽丆侽乯丄乮俆丆侾丆侽乯丄乮係丆俀丆侽乯丄乮俁丆俁丆侽乯丄乮俀丆係丆侽乯丄乮侾丆俆丆侽乯丄
丂丂乮侽丆俇丆侽乯
丂敀乮侾丆侽丆俀乯偵懳偟偰丄崟乮俇丆侽丆侽乯丄乮俆丆侽丆侾乯丄乮係丆侽丆俀乯丄乮俁丆侽丆俁乯丄乮俀丆侽丆係乯丄
丂丂乮侾丆侽丆俆乯丄乮侽丆侽丆俇乯
丂敀乮侽丆俁丆侽乯偵懳偟偰丄崟乮俇丆侽丆侽乯丄乮俆丆侾丆侽乯丄乮係丆俀丆侽乯丄乮俁丆俁丆侽乯丄乮俀丆係丆侽乯丄
丂丂乮侾丆俆丆侽乯丄乮侽丆俆丆侾乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄乮侽丆俀丆係乯丄乮侽丆侾丆俆乯丄乮侽丆侽丆俇乯
丂敀乮侽丆俀丆侾乯偵懳偟偰丄崟乮侽丆俇丆侽乯丄乮侽丆俆丆侾乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄乮侽丆俀丆係乯丄
丂丂乮侽丆侾丆俆乯丄乮侽丆侽丆俇乯
丂敀乮侽丆侾丆俀乯偵懳偟偰丄崟乮侽丆俇丆侽乯丄乮侽丆俆丆侾乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄乮侽丆俀丆係乯丄
丂丂乮侽丆侾丆俆乯丄乮侽丆侽丆俇乯
丂敀乮侽丆侽丆俁乯偵懳偟偰丄崟乮俇丆侽丆侽乯丄乮俆丆侽丆侾乯丄乮係丆侽丆俀乯丄乮俁丆侽丆俁乯丄乮俀丆侽丆係乯丄
丂丂乮侾丆侽丆俆乯丄乮侽丆俇丆侽乯丄乮侽丆俆丆侾乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄乮侽丆俀丆係乯丄乮侽丆侾丆俆乯
丂傛偭偰丄俁偮偺敔偺偆偪偱壗傟偐偑嬻偵側傞応崌偺悢偼丄丂俁亄俈俉亖俉侾乮捠傝乯
丂埲忋偐傜丄偳偺敔偵傕彮側偔偲傕侾屄埲忋嬍偑擖傞暘偗曽偺悢偼丄
丂丂俀俉侽亅俉侾亖侾俋俋乮捠傝乯
乮暿夝乯丂敔俙偑嬻偱丄俛偲俠偵偼彮側偔偲傕侾屄埲忋嬍偑擖傞暘偗曽偺悢偼丄
丂2俫3亊2俫6亅俀亖係亊俈亅俀亖俀俇乮捠傝乯
丂敔俛偑嬻偱丄俙偲俠偵偼彮側偔偲傕侾屄埲忋嬍偑擖傞暘偗曽偺悢偼丄俀俇乮捠傝乯
丂敔俠偑嬻偱丄俙偲俛偵偼彮側偔偲傕侾屄埲忋嬍偑擖傞暘偗曽偺悢偼丄俀俇乮捠傝乯
丂敔俙偲俛丄俛偲俠丄俙偲俠偑嬻偵側傞応崌偼丄俁捠傝
丂偟偨偑偭偰丄偳偺敔偵傕彮側偔偲傕侾屄埲忋嬍偑擖傞暘偗曽偺悢偼丄
丂丂俀俉侽亅俀俇亊俁亅俁亖侾俋俋乮捠傝乯
乮俁乯丂偳偺敔偵傕敀嬍偑俀屄埲忋傑偨偼崟嬍偑俀屄埲忋擖傞暘偗曽偼丄
丂敀乮俁丆侽丆侽乯偵懳偟偰丄崟乮俀丆俀丆俀乯丄乮侾丆俁丆俀乯丄乮侾丆俀丆俁乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄
丂丂乮侽丆俀丆係乯
丂敀乮俀丆侾丆侽乯偵懳偟偰丄崟乮俀丆俀丆俀乯丄乮侾丆俁丆俀乯丄乮侾丆俀丆俁乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄
丂丂乮侽丆俀丆係乯
丂敀乮俀丆侽丆侾乯偵懳偟偰丄崟乮俀丆俀丆俀乯丄乮侾丆俁丆俀乯丄乮侾丆俀丆俁乯丄乮侽丆係丆俀乯丄乮侽丆俁丆俁乯丄
丂丂乮侽丆俀丆係乯
丂敀乮侾丆俀丆侽乯偵懳偟偰丄崟乮係丆侽丆俀乯丄乮俁丆侾丆俀乯丄乮俁丆侽丆俁乯丄乮俀丆俀丆俀乯丄乮俀丆侾丆俁乯丄
丂丂乮俀丆侽丆係乯
丂敀乮侾丆侾丆侾乯偵懳偟偰丄崟乮俀丆俀丆俀乯
丂敀乮侾丆侽丆俀乯偵懳偟偰丄崟乮係丆俀丆侽乯丄乮俁丆俁丆侽乯丄乮俁丆俀丆侾乯丄乮俀丆係丆侽乯丄乮俀丆俁丆侾乯丄
丂丂乮俀丆俀丆俀乯
丂敀乮侽丆俁丆侽乯偵懳偟偰丄崟乮係丆侽丆俀乯丄乮俁丆侾丆俀乯丄乮俁丆侽丆俁乯丄乮俀丆俀丆俀乯丄乮俀丆侾丆俁乯丄
丂丂乮俀丆侽丆係乯
丂敀乮侽丆俀丆侾乯偵懳偟偰丄崟乮係丆侽丆俀乯丄乮俁丆侾丆俀乯丄乮俁丆侽丆俁乯丄乮俀丆俀丆俀乯丄乮俀丆侾丆俁乯丄
丂丂乮俀丆侽丆係乯
丂敀乮侽丆侾丆俀乯偵懳偟偰丄崟乮係丆俀丆侽乯丄乮俁丆俁丆侽乯丄乮俁丆俀丆侾乯丄乮俀丆係丆侽乯丄乮俀丆俁丆侾乯丄
丂丂乮俀丆俀丆俀乯
丂敀乮侽丆侽丆俁乯偵懳偟偰丄崟乮係丆俀丆侽乯丄乮俁丆俁丆侽乯丄乮俁丆俀丆侾乯丄乮俀丆係丆侽乯丄乮俀丆俁丆侾乯丄
丂丂乮俀丆俀丆俀乯
丂埲忋偐傜丄媮傔傞応崌偺悢偼丄丂俋亊俇亄侾亖俆俆乮捠傝乯
乮暿夝乯丂梊傔敔俙偵敀俀屄丄敔俛偲俠偵崟俀屄偢偮傪擖傟偰偍偔偲偒丄
丂巆傝敀侾屄偺擖傟曽偼丄俁捠傝偱丄
丂偦偺侾捠傝偵懳偟偰丄巆傝崟俀屄偺擖傟曽偼丄3俫2亖俇乮捠傝乯丂側偺偱丄俁亊俇亖侾俉乮捠傝乯
摨條偵丄梊傔敔俛偵敀俀屄丄敔俙偲俠偵崟俀屄偢偮傪擖傟偰偍偔偲偒丄侾俉乮捠傝乯
丂梊傔敔俠偵敀俀屄丄敔俙偲俛偵崟俀屄偢偮傪擖傟偰偍偔偲偒丄侾俉乮捠傝乯
丂梊傔敔俙丄俛丄俠偵敀侾屄偢偮擖傟偨応崌偼丄崟俇屄傪敔俙丄俛丄俠偵崟俀屄偢偮擖傟傞昁梫
偑偁傞偺偱丄偙傟偑侾捠傝偁傞丅
丂傛偭偰丄媮傔傞応崌偺悢偼丄丂俁亊侾俉亄侾亖俆俆乮捠傝乯
嘫丏丂倶倷 暯柺偵偍偄偰丄嬋慄 倷亖倱倝値 倶 偲 倷亖倎丒倱倝値乮倶/俀乯 偑偁傞丅偨偩偟丄倎 偼幚悢偺掕悢
丂丂偱偁傝丄倶 偺庢傝摼傞斖埻偼丄侽亝倶亝俀兾偱偁傞丅偙偺俀嬋慄偼丄侽亙倶亙俀兾偺斖埻偵偍
丂丂偄偰丄偨偩堦偮岎揰傪帩偮傕偺偲偟丄偦偺岎揰偺 倶 嵗昗傪 倶0 偲偡傞丅偙偺偲偒丄偙偺俀嬋
丂丂慄偱埻傑傟傞恾宍偼俀偮偁傝丄倷 幉偲捈慄 倶亖倶0 偱嫴傑傟傞曽偺柺愊傪俽1丄傕偆堦曽偺
丂丂柺愊傪俽2偲偡傞丅俽1亖係俽2 偱偁傞偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂倎 傪 倶0 偱昞偣丅
乮俀乯丂倎 偺抣傪媮傔傛丅
乮夝乯乮侾乯丂倱倝値 倶 亖倎丒倱倝値乮倶/俀乯 傛傝丄丂俀倱倝値乮倶/俀乯們倧倱乮倶/俀乯亖倎丒倱倝値乮倶/俀乯
丂侽亙倶亙俀兾傛傝丄丂侽亙倶/亙兾丂側偺偱丄丂倱倝値乮倶/俀乯亗侽
丂傛偭偰丄丂倎亖俀們倧倱乮倶0/俀乯
乮俀乯丂俽1亖佺0倶0 乮倱倝値 倶 亅倎丒倱倝値乮倶/俀乯乯倓倶亖[亅們倧倱 倶 亄俀倎丒們倧倱乮倶/俀乯]0倶0
丂丂丂丂亖亅們倧倱 倶 0亄俀倎丒們倧倱乮倶0/俀乯亄侾亅俀倎
丂丂丂丂亖亅們倧倱 倶 0亄係們倧倱2乮倶0/俀乯亄侾亅俀倎
丂丂丂丂亖亅們倧倱 倶 0亄俀亄俀們倧倱 倶 0亄侾亅俀倎亖俁亅俀倎亄們倧倱 倶 0
丂俽2亖佺倶02兾 乮倎丒倱倝値乮倶/俀乯亅倱倝値 倶 乯倓倶亖[亅俀倎丒們倧倱乮倶/俀乯亄們倧倱 倶 ]倶02兾
丂丂丂丂亖俀倎亄侾亄俀倎丒們倧倱乮倶0/俀乯亅們倧倱 倶0
丂丂丂丂亖俀倎亄侾亄係們倧倱2乮倶0/俀乯亅們倧倱 倶0
丂丂丂丂亖俀倎亄侾亄俀亄俀們倧倱 倶0亅們倧倱 倶0亖俀倎亄俁亄們倧倱 倶0
俽1亖係俽2 傛傝丄丂俁亅俀倎亄們倧倱 倶 0亖係乮俀倎亄俁亄們倧倱 倶0乯丂側偺偱丄
丂侾侽倎亄俋亄俁們倧倱 倶0亖侽
丂偙偙偱丄丂們倧倱 倶0亖俀們倧倱2乮倶0/俀乯亅侾亖倎2/俀亅侾丂側偺偱丄丂俁倎2/俀亄侾侽倎亄俇亖侽
丂偡側傢偪丄丂俁倎2亄俀侽倎亄侾俀亖侽丂偐傜丄乮俁倎亄俀乯乮倎亄俇乯亖侽丂傛傝丄倎亖亅俀/俁丄亅俇
丂偙偙偱丄倎亖俀們倧倱乮倶0/俀乯丂偐傜丄丂亅俀亝倎亝俀丂側偺偱丄丂倎亖亅俀/俁丂丂乮廔乯
嘮丏丂倶倷倸 嬻娫偵揰俷傪拞怱偲偡傞敿宎俀偺媴柺俽偑偁傝丄俽忋偵堎側傞俁揰俙丄俛丄俠傪偲傞丅
丂丂偙偙偱丄仮俙俛俠偼 倶倷 暯柺忋偵偁傞惓嶰妏宍偱丄揰俙偺嵗昗偼乮俀丆侽丆侽乯偱偁傝丄揰俛偺
丂丂 倷 嵗昗偺抣偑惓偱偁傞偲偡傞丅俽忋偵偁傞揰俹偑丄佢俛俷俹亖兾/俇 偲偄偆忦審傪枮偨偟偰
丂丂摦偔偲偒丄倸 嵗昗偺抣偑嵟彫偱偁傞傛偆側揰俹傪俹1偲偡傞丅偙偺偲偒丄埲壓偺栤偄偵摎偊傛丅
乮侾乯丂俹1偺嵗昗傪媮傔傛丅
乮俀乯丂俽忋偵偁傞揰俻偑佢俻俷俹1亖兾/俇偲偄偆忦審傪枮偨偟偰摦偔偲偒丄慄暘俙俻偺挿偝偑嵟
丂丂彫偲側傞揰俻傪俻1偲偡傞丅偙偺偲偒丄嶰妏悕俙俛俠俻1偺懱愊偼偄偔傜偐丅
丂丂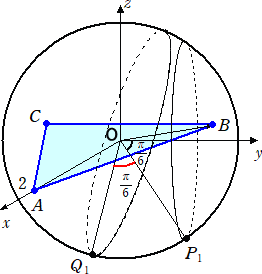
乮夝乯乮侾乯丂戣堄傛傝丄俛乮亅侾丆![]() 丆侽乯丄俠乮亅侾丆亅
丆侽乯丄俠乮亅侾丆亅![]() 丆侽乯偱偁傞丅揰俹傛傝丄慄暘俷俛偵壓
丆侽乯偱偁傞丅揰俹傛傝丄慄暘俷俛偵壓
丂傠偟偨悅慄偺懌傪俷乫偲偍偔偲丄丂俷俷乫亖![]() 丂丄俹俷乫亖侾丂偱偁傞丅
丂丄俹俷乫亖侾丂偱偁傞丅
丂偙偺偲偒丄俷乫偺嵗昗偼丄乮![]() /俀乯乮亅侾丆
/俀乯乮亅侾丆![]() 丆侽乯亖乮亅
丆侽乯亖乮亅![]() /俀丆俁/俀丆侽乯丂偲側傞丅
/俀丆俁/俀丆侽乯丂偲側傞丅
丂戣堄傛傝丄丂俹1乮亅![]() /俀丆俁/俀丆亅侾乯丂偱偁傞丅
/俀丆俁/俀丆亅侾乯丂偱偁傞丅
乮俀乯丂乮侾乯偲摨條偵丄揰俻傛傝慄暘俷俹1偵壓傠偟偨悅慄偺懌傪俷乭偲偍偔偲丄
丂俷俷乭亖![]() 丂丄俻俷乭亖侾丂偱偁傞丅偙偺偲偒丄揰俷乭偺嵗昗偼丄
丂丄俻俷乭亖侾丂偱偁傞丅偙偺偲偒丄揰俷乭偺嵗昗偼丄
丂乮![]() /俀乯乮亅
/俀乯乮亅![]() /俀丆俁/俀丆亅侾乯亖乮亅俁/係丆俁
/俀丆俁/俀丆亅侾乯亖乮亅俁/係丆俁![]() /係丆亅
/係丆亅![]() /俀乯丂偲側傞丅
/俀乯丂偲側傞丅
丂俻乮倶丆倷丆倸乯偲偍偔偲丄俻偼俽忋偺揰側偺偱丄丂倶2亄倷2亄倸2亖係
偝傜偵丄俻俷乭亖侾丂側偺偱丄丂乮倶亄俁/係乯2亄乮倷亅俁![]() /係乯2亄乮倸亄
/係乯2亄乮倸亄![]() /俀乯2亖侾
/俀乯2亖侾
丂偙偺偲偒丄丂侾亅乮倶亄俁/係乯2亖乮倷亅俁![]() /係乯2亄乮倸亄
/係乯2亄乮倸亄![]() /俀乯2亞侽丂傛傝丄
/俀乯2亞侽丂傛傝丄
丂亅俈/係亝倶亝侾/係丂偱偁傞丅
丂戣堄傛傝丄慄暘俙俻偺挿偝偑嵟彫偲側傞揰俻偑俻1側偺偱丄
丂俙俻2亖乮倶亅俀乯2亄倷2亄倸2亖倶2亄倷2亄倸2亅係倶亄係亖俉亅係倶丂偼丄倶亖侾/係丂偺偲偒嵟彫
偙偺偲偒丄丂倷亖俁![]() /係丂丄倸亖亅
/係丂丄倸亖亅![]() /俀丂傛傝丄丂俻1乮侾/係丆俁
/俀丂傛傝丄丂俻1乮侾/係丆俁![]() /係丆亅
/係丆亅![]() /俀乯丂偲側傞丅
/俀乯丂偲側傞丅
丂廬偭偰丄媮傔傞嶰妏悕俙俛俠俻1偺懱愊偼丄
丂丂乮侾/俁乯丒仮俙俛俠丒乮![]() /俀乯亖乮侾/俁乯丒乮
/俀乯亖乮侾/俁乯丒乮![]() /係乯乮俀
/係乯乮俀![]() 乯2丒乮
乯2丒乮![]() /俀乯亖俁/俀丂丂乮廔乯
/俀乯亖俁/俀丂丂乮廔乯
丂丂埲壓丄岺帠拞両