| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽係俈 | 暯惉俁侽擭搙慜婜 | 丂搶杒戝妛丂 | 丂棟宯 | 丒丒丒 | 嶰妏娭悢乮悢嘥嘦乯 | 丂傗傗擄 |
丂寁嶼検偑懡偔丄恾帵傗徹柧傪梫媮偡傞栤戣偑懡偐偭偨傛偆偱偡丅
搶杒戝妛丂慜婜棟宯乮俀侽侾俉乯
丂嶰妏宍ABC偺撪愙墌偺敿宎傪 倰 丄奜愙墌偺敿宎傪俼偲偟丄倛亖倰/俼偲偡傞丅
傑偨丄佢A亖俀兛丄佢俛亖俀兝丄佢俠亖俀兞偲偍偔丅
乮侾乯丂倛亖係sin兛sin兝sin兞丂偲側傞偙偲傪帵偣丅
乮俀乯丂嶰妏宍ABC偑捈妏嶰妏宍偺偲偒丄倛亝![]() 亅侾丂偑惉傝棫偮偙偲傪帵偣丅傑偨丄摍崋偑
亅侾丂偑惉傝棫偮偙偲傪帵偣丅傑偨丄摍崋偑
丂丂惉傝棫偮偺偼偳偺傛偆側応崌偐丅
乮俁乯丂堦斒偺嶰妏宍ABC偵懳偟偰丄倛亝侾/俀丂偑惉傝棫偮偙偲傪帵偣丅傑偨丄摍崋偑惉傝棫偮
丂丂偺偼偳偺傛偆側応崌偐丅
乮嶲峫乯丂倛偺昡壙傪栤偆摨庯巪偺栤戣偑丄嫗搒戝妛丂屻婜棟宯乮俀侽侽俇乯偱弌戣偝傟偰偄傞丅
| 乮夝乯 | 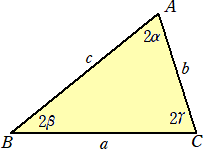 |
乮侾乯丂嵍恾偵偍偄偰丄丂倱亖乮倎亄倐亄們乯/俀丂偲偍偔偲丄 丂仮ABC偺柺愊俽偼丄俽亖倰丒倱亖倎倐們/(係俼)丂偲彂偗傞丅 丂丂惓尫掕棟傛傝丄 丂丂倎亖俀俼sin俀兛丄倐亖俀俼sin俀兝丄們亖俀俼sin俀兞 |
丂丂傛偭偰丄丂倰亖俀俼sin俀兛丒sin俀兝丒sin俀兞/乮sin俀兛亄sin俀兝亄sin俀兞乯丂傛傝丄
丂丂倛亖倰/俼亖俀sin俀兛丒sin俀兝丒sin俀兞/乮sin俀兛亄sin俀兝亄sin俀兞乯
丂丂丂亖侾俇sin兛sin兝sin兞丒cos兛cos兝cos兞/乮sin俀兛亄sin俀兝亄sin俀兞乯
丂偙偙偱丄丂俀兛亄俀兝亄俀兞亖兾丂側偺偱丄
丂sin俀兛亄sin俀兝亄sin俀兞亖俀sin乮兛亄兝乯們倧倱乮兛亅兝乯亄俀sin兞cos兞
亖俀cos兞們倧倱乮兛亅兝乯亄俀sin兞cos兞亖俀cos兞乮們倧倱乮兛亄兝乯亄cos乮兛亅兝乯乯
亖係cos兛cos兝cos兞
丂傛偭偰丄丂倛亖係sin兛sin兝sin兞
乮俀乯丂俀兞亖兾/俀丂懄偪丄兞亖兾/係丂偲壖掕偟偰傕堦斒惈傪幐傢側偄丅偙偺偲偒丄
丂倛亖亅俀sin兞乮們倧倱乮兛亄兝乯亅cos乮兛亅兝乯乯亖亅![]() 乮
乮![]() /俀亅cos乮兛亅兝乯乯
/俀亅cos乮兛亅兝乯乯
傛傝丄丂倛亖![]() cos乮兛亅兝乯亅侾亝
cos乮兛亅兝乯亅侾亝![]() 亅侾
亅侾
丂摍崋惉棫偼丄兛亅兝亖侽丂懄偪丄兛亖兝亖兾/俉丂偺偲偒偵尷傞丅
丂偙偺偲偒丄嶰妏宍ABC偼捈妏俀摍曈嶰妏宍偱偁傞丅
乮俁乯丂堦斒偵丄
丂倛亖亅俀sin兞乮們倧倱乮兛亄兝乯亅cos乮兛亅兝乯乯亖亅俀sin兞乮sin兞亅cos乮兛亅兝乯乯丂傛傝丄
丂丂丂倛亖俀sin兞cos乮兛亅兝乯亅俀sin2兞
丂偙偙偱丄丂亅兾/俀亙兛亅兝亙兾/俀丄侽亙兞亙兾/俀丂側偺偱丄
丂丂丂侽亙cos乮兛亅兝乯亝侾丂丄丂侽亙sin兞亙侾
丂傛偭偰丄丂倛亝俀sin兞亅俀sin2兞亖亅俀乮sin兞亅侾/俀乯2亄侾/俀亝侾/俀
丂摍崋惉棫偼丄兛亅兝亖侽丂偐偮丂兞亖兾/俇丂懄偪丄兛亖兝亖兞亖兾/俇丂偺偲偒偵尷傞丅
丂偙偺偲偒丄嶰妏宍ABC偼惓嶰妏宍偱偁傞丅