０４３	平成２９年度前期	東京大学	文系	・・・	ベクトル（数Ｂ）	易

　今年の東京大学の問題は、定型的な問題が多く取り組みやすかったらしい。数学の出来
る方がそれなりの点数が取れるということでメデタシ、メデタシ。昨年度からの傾向で難関大
学の問題レベルが易化しているのだろうか？


東京大学　前期文系（２０１７）

　１辺の長さが１の正六角形ＡＢＣＤＥＦが与えられている。点Ｐが辺ＡＢ上を、点Ｑが辺ＣＤ
上をそれぞれ独立に動くとき、線分ＰＱを２：１に内分する点Ｒが通りうる範囲の面積を求め
よ。

（解）


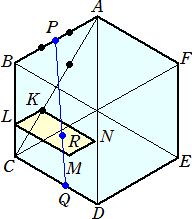
　ＡＢ＝ａ　、ＡＦ＝ｂ　とおき、　ＡＰ＝ｓａ　（０≦ｓ≦１）　、

　ＣＱ＝ｔｂ　（０≦ｔ≦１）　とおく。

　このとき、　ＡＱ＝ａ＋（ａ＋ｂ）＋ｔｂ＝２ａ＋ｂ＋ｔｂ　なので、

　ＡＲ＝（ｓａ＋４ａ＋２ｂ＋２ｔｂ）/３

　　　＝（４ａ＋２ｂ）/３＋（ｓａ＋２ｔｂ）/３




　すなわち、　ＡＲ＝ＡＫ＋ｓＫＬ＋ｔＫＮ　より、点Ｒは、１辺の長さが１/３、２/３でその間の
角が１２０°の平行四辺形上を動く。

　よって、求める面積は、　（１/３）（２/３）ｓｉｎ１２０°＝/９　　（終）