| |
||||||
| 036 | 平成27年度前期 | 東京大学 | 文系 | ・・・ | 図形と式(数Ⅱ) | やや難 |
今年度の東京大学の入試問題は全般的に難しかったと言われる。特に、文系がその傾向
だったように感じる。理系並みの数学の力が要求されているようだ。
東京大学 前期文系(2015)
Lを座標平面上の原点を通り傾きが正の直線とする。さらに、以下の3条件(ⅰ)、(ⅱ)、
(ⅲ)で定まる円C1、C2を考える。
(ⅰ) 円C1、C2は2つの不等式 x≧0、y≧0 で定まる領域に含まれる。
(ⅱ) 円C1、C2は直線Lと同一点で接する。
(ⅲ) 円C1 は x 軸と点(1,0)で接し、円C2 はy軸と接する。
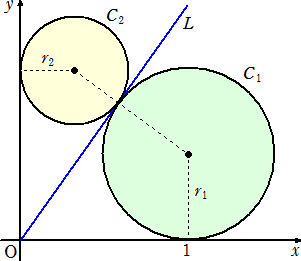
円C1 の半径を r1 、円C2 の半径を r2 とする。 8r1 +9r2 が最小となるような直線Lの
方程式と、その最小値を求めよ。
(解) 題意より、中心C1(1,r1)、C2(r2,1) とおける。このとき、
(1-r2)2+(t-r1)2=(r1+r2)2 より、 r2=(1-r1)/(1+r1) である。
よって、 8r1 +9r2=8r1 +9(1-r1)/(1+r1)=(8r12-r1+9)/(1+r1)
ここで、1+r1=t とおくと、t≧1で、8r1 +9r2=8t+18/t-17
相加平均と相乗平均の関係から、 8t+18/t≧2√(8×18)=24 で、
等号成立は、 8t=18/t すなわち、 t=3/2 のとき。
このとき、 r1=1/2、r2=1/3 で、最小値は、7 である。
また、8r1 +9r2 が最小となるような直線Lの方程式Lは、C1(1,1/2)、C2(1/3,1)
を結ぶ直線に垂直なので、 L: y=4/3x である。 (終)
(コメント) 予備校等の分析では「やや難」であるが、標準的な良問であった。