| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俁俆 | 暯惉俀俈擭搙慜婜 | 丂搶嫗戝妛丂 | 丂暥宯 | 丒丒丒 | 俀師娭悢乮悢嘥嘦乯 | 丂傗傗擄 |
丂崱擭搙偺搶嫗戝妛偺擖帋栤戣偼慡斒揑偵擄偟偐偭偨偲尵傢傟傞丅摿偵丄暥宯偑偦偺孹岦
偩偭偨傛偆偵姶偠傞丅棟宯暲傒偺悢妛偺椡偑梫媮偝傟偰偄傞傛偆偩丅
搶嫗戝妛丂慜婜暥宯乮俀侽侾俆乯
丂嵗昗暯柺忋偺俀揰俙乮亅侾丆侾乯丄俛乮侾丆亅侾乯傪峫偊傞丅傑偨丄俹傪嵗昗暯柺忋偺揰偲偟丄偦偺
倶嵗昗偺愨懳抣偼侾埲壓偱偁傞偲偡傞丅
丂師偺忦審乮鶣乯傑偨偼乮鶤乯傪傒偨偡揰俹偺斖埻傪恾帵偟丄偦偺柺愊傪媮傔傛丅
乮鶣乯丂捀揰偺倶嵗昗偺愨懳抣偑侾埲忋偺俀師娭悢偺僌儔僼偱丄揰俙丄俹丄俛傪偡傋偰捠傞傕偺
丂丂丂偑偁傞丅
乮鶤乯丂揰俙丄俹丄俛偼摨堦捈慄忋偵偁傞丅
乮夝乯丂俁揰俙丄俹丄俛偑摨堦捈慄忋偵偁傞偲偒丄揰俙丄俹丄俛傪偡傋偰捠傞俀師娭悢偺僌儔僼偼
丂丂丂懚嵼偟側偄偺偱丄乮鶣乯傪傒偨偡揰俹偺斖埻傪媮傔傞応崌丄俁揰俙丄俹丄俛偼摨堦捈慄忋
丂丂丂偵側偄傕偺偲偟偰傛偄丅
丂戣堄傛傝丄揰俹乮倱丆倲乯丂乮亅侾亝倱亝侾乯丂偲偍偗傞丅
丂揰俹偑忦審乮鶤乯傪傒偨偡偲偒丄丂倲亖亅倱丂偑惉傝棫偮丅
丂揰俹偑忦審乮鶣乯傪傒偨偡偲偒傪峫偊傞丅俁揰俙丄俹丄俛傪偡傋偰捠傞曻暔慄偺曽掱幃傪
丂丂倷亖倎倶2亄倐倶亄們
偲偍偔偲丄倎亅倐亄們亖侾丂丄倎亄倐亄們亖亅侾丂傛傝丄丂倐亖亅侾丄丂們亖亅倎丂偲側傞丅偡側傢偪丄
丂丂倷亖倎倶2亅倶亅倎
丂捀揰偺倶嵗昗偼丄丂侾/乮俀倎乯丂側偺偱丄戣堄傛傝丄丂侾/乮俀倎乯亝亅侾丄侾/乮俀倎乯亞侾
丂偡側傢偪丄丂亅侾/俀亝倎亙侽丄侽亙倎亝侾/俀
丂偙偙偱丄丂倎倱2亅倱亅倎亖倲丂傛傝丄丂倎乮倱2亅侾乯亖倱亄倲
丂朻摢偱偺妋擣偐傜丄丂倱2亅侾亗侽丂偲偟偰傛偄偺偱丄丂倎亖乮倱亄倲乯/乮倱2亅侾乯
傛偭偰丄丂亅侾/俀亝乮倱亄倲乯/乮倱2亅侾乯亙侽丄侽亙乮倱亄倲乯/乮倱2亅侾乯亝侾/俀
丂亅侾亝倱亝侾丂傛傝丄丂倱2亅侾亙侽丂側偺偱丄
丂丂侽亙倱亄倲亝亅乮倱2亅侾乯/俀丂丄丂乮倱2亅侾乯/俀亝倱亄倲亙侽
偟偨偑偭偰丄丂倲亜亅倱丂偐偮丂倲亝乮亅侾/俀乯乮倱亄侾乯2亄侾
丂丂丂丂丂丂丂傑偨偼丄丂倲亙亅倱丂偐偮丂倲亞乮侾/俀乯乮倱亅侾乯2亅侾
丂忋婰偲丄倲亖亅倱丂乮亅侾亝倱亝侾乯丂傪崌傢偣偰丄壓恾偺椞堟偑媮傔傞傕偺偱偁傞丅
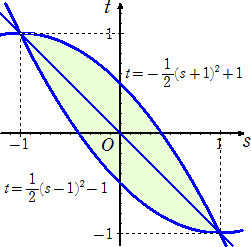 丂丂丂傛偭偰丄媮傔傞柺愊偼丄
丂丂丂傛偭偰丄媮傔傞柺愊偼丄
丂丂乮侾/侾俀乯丒係3丒乮侾/俀乯亊俀亅係
丂丂亖侾俇/俁亅係亖係/俁丂丂乮廔乯
乮僐儊儞僩乯丂梊旛峑偺擄堈暘愅偱偼乽傗傗擄乿偲側偭偰偄傞偑丄偙傟偼庴尡惗偑惂尷帪娫埲撪
丂丂丂丂丂丂偱偳偺掱搙弌棃傞偐偺栚埨丅撪梕揑偵偼懡暘乽昗弨乿儗儀儖偺栤戣偩傠偆偲巚偆丅
丂丂丂丂丂丂丂柺愊偺寁嶼偱椺偺岞幃傪梡偄偨偑丄杮斣偺摎埬偱偼尭揰偺儕僗僋傪旔偗傞偨傔
丂丂丂丂丂丂偵丄慺捈偵愊暘寁嶼偟偨曽偑柍擄偩傠偆丅