| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俀俀 | 暯惉俀侾擭搙慜婜 | 墶昹崙棫戝妛 | 岺妛晹 | 丒丒丒 | 旝暘愊暘乮悢妛嘨乯 | 丂昗弨 |
丂偙偺栤戣偼丄傂偨偡傜寁嶼偱丄庴尡惗偺崻婥偲擡懴偑帋偝傟傞栤戣偲尵偊傛偆丅
墶昹崙棫戝妛丂岺妛晹慜婜乮俀侽侽俋乯
丂暯柺忋偵俁揰 俷 丄俙 丄俛 偑偁傝丄俷俙亖a 丄俷俛亖倐丂乮侽亙倎亙倐乯丂偱 俷俙偲俷俛偺側偡妏兤
偼 侽亙兤亝兾/俀丂傪傒偨偡丅揰俠傪丂俷俠亖俷俙亄俷俛偱掕傔傞丅傑偨丄俷偐傜堷偄偨敿捈慄
俷俙忋偵揰俹傪 俷俙亙俷俹 偲側傞傛偆偵偲傞丅捈慄俹俠偲捈慄俷俛偺岎揰傪俻偲偟丄俙俹亖倶
丄
俹俻2亖俥乮倶乯 偲偡傞偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂俥乮倶乯 傪 倶 丆 倎 丆 倐 丆 兤 傪梡偄偰昞偣丅
乮俀乯丂戞俀師摫娭悢 俥乭乮倶乯 偼 倶 亜侽 偺偲偒俥乭乮倶乯亜侽 傪傒偨偡偙偲傪帵偣丅
乮俁乯丂倎亖侾丄倐亖![]() 丄們倧倱兤亖侾/
丄們倧倱兤亖侾/![]() 丂偺偲偒丄俹俻偺挿偝偺嵟彫抣傪媮傔傛丅
丂偺偲偒丄俹俻偺挿偝偺嵟彫抣傪媮傔傛丅
乮夝乯丂乮侾乯丂
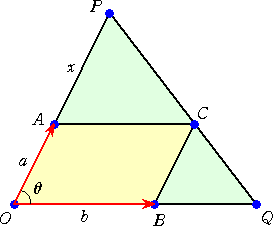 丂丂嵍恾偵偍偄偰丄
丂丂嵍恾偵偍偄偰丄
丂丂丂俷俹亖乮乮倶亄倎乯/倎乯俷俙丂偼柧傜偐丅
丂傑偨丄丂俛俻 丗 倐亄俛俻 亖 倎 丗 倶亄倎丂傛傝丄
丂丂丂俛俻亖倎倐/倶丂偲側傞丅
丂傛偭偰丄丂俷俻亖倐亄倎倐/倶亖倐乮倶亄倎乯/倶丂傛傝丄
丂丂丂俷俻亖乮乮倶亄倎乯/倶乯俷俛
丂偙偺偲偒丄丂俥乮倶乯亖俹俻2亖乥俷俻亅俷俹乥2亖乮倶亄倎乯2乮倶2亅俀倐倶們倧倱兤亄倐2乯/倶2丂偲側傞丅
乮俀乯丂俥乫乮倶乯亖俀乷倶4亄乮倎亅倐們倧倱兤乯倶3亄倎倐乮倎們倧倱兤亅倐乯倶亅倎2倐2乸/倶3
丂丂丂俥乭乮倶乯亖俀乷倶4亄俀倎倐2倶亅俀倎2倐倶們倧倱兤亄俁倎2倐2乸/倶4
丂丂丂丂丂丂丂亖俀乷倶4亄俀倎2倐乮侾亅們倧倱兤乯倶亄俀倎倐乮倐亅倎乯倶亄俁倎2倐2乸/倶4
丂丂偙偺偲偒丄丂倶亜侽丂偵偍偄偰丄丂侾亅們倧倱兤亞侽丂丄丂倐亅倎亜侽丂偐傜丄丂俥乭乮倶乯亜侽
丂丂乮俥乫乮倶乯偺寁嶼偑寢峔戝曄偱偟偨両乯
乮俁乯丂忦審傛傝丄
丂丂丂丂俥乮倶乯亖乮倶亄侾乯2乮倶2亅俀倶亄俇乯/倶2亖乮倶4亄俁倶2亄侾侽倶亄俇乯/倶2
丂丂側偺偱丄丂俥乫乮倶乯亖俀乮倶亄侾乯乮倶亅俀乯乮倶2亄倶亄俁乯/倶3亖侽丂傛傝丄丂倶亖俀
丂丂倶亖俀丂偺偲偒丄丂俥乮倶乯偼嬌彫偐偮嵟彫偲側傝丄嵟彫抣偼丂俀俈/俀
丂丂傛偭偰丄俹俻偺嵟彫抣偼丄丂俁![]() /俀丂偲側傞丅丂丂乮廔乯
/俀丂偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂忋婰偱偼丄堄恾揑偵嬌椡搑拞寁嶼傪徣棯偟偰傒偨丅夝朄揑偵偼嫵壢彂儗儀儖
丂丂丂丂丂丂偱偁傝丄壗傜擄偟偄偙偲傪暦偄偰偄側偄偙偲傪妋擣偟偰傕傜偆偨傔偱偁傞丅
丂丂丂丂丂丂丂丂偟偐偟丄堦搙帺暘偱忋婰偺寁嶼傪傗偭偰傒傞偲丄寵婥偑偝偡偔傜偄偵戝曄側寁
丂丂丂丂丂丂嶼検偵埑搢偝傟傞偼偢偱偁傞丅偁傞幰偼搑拞偱寁嶼傪曻傝弌偟偰偟傑偆偐傕偟傟
丂丂丂丂丂丂側偄丅
丂丂丂丂丂丂丂丂墶崙偼墲乆偵偟偰丄偙偺傛偆側寁嶼椡傪栤偆栤戣偑偍岲偒側傛偆偩丅墶巗傕偦
丂丂丂丂丂丂偆偐側丠
丂梊旛峑偑岞奐偟偰偄傞夝摎傪嶲峫偵偡傟偽丄俥乮倶乯傪丄
丂俥乮倶乯亖乮侾亄俀倎/倶亄倎2/倶2乯乮倶2亅俀倐倶們倧倱兤亄倐2乯
丂丂丂丂亖倶2亅俀倐倶們倧倱兤亄倐2亄俀倎乮倶亅俀倐們倧倱兤亄倐2/倶乯亄倎2亅乮俀倎2倐們倧倱兤乯/倶亄倎2倐2/倶2
偺宍偵揥奐偟偰偐傜戞俀師摫娭悢傪寁嶼偡傞曽偑妝側傛偆偩両
丂幚嵺偵丄丂俥乫乮倶乯亖俀倶亅俀倐們倧倱兤亄俀倎乮侾亅倐2/倶2乯亄乮俀倎2倐們倧倱兤乯/倶2亅俀倎2倐2/倶3
丂丂丂丂丂丂丂俥乭乮倶乯亖俀亄係倎倐2/倶3亅係倎2倐們倧倱兤/倶3亄俇倎2倐2/倶4
丂丂丂丂丂丂丂丂丂丂丂亖俀乷倶4亄俀倎倐2倶亅俀倎2倐倶們倧倱兤亄俁倎2倐2乸/倶4
偲側傞丅屻偼丄杮夝偲摨條偵丄
丂丂丂丂丂丂丂俥乭乮倶乯亖俀乷倶4亄俀倎2倐乮侾亅們倧倱兤乯倶亄俀倎倐乮倐亅倎乯倶亄俁倎2倐2乸/倶4
偲幃曄宍偟偰丄丂俥乭乮倶乯亜侽丂偑帵偝傟傞丅
乮僐儊儞僩乯丂榬椡傪夁怣偟偰丄愊偺摫娭悢丒彜偺摫娭悢偺岞幃偱偖傝偖傝寁嶼偡傞傛傝傕丄寉
丂丂丂丂丂丂柇偵揥奐偟偰寉偔偐傢偡寁嶼偑偲偰傕偍偟傖傟偱偡偹両
丂乮侾乯偱丄梋尫掕棟偐傜丄
丂丂丂丂丂丂丂丂俥乮倶乯亖乮倶亄倎乯2亄倐2乮倶亄倎乯2/倶2亅俀倐們倧倱兤乮倶亄倎乯2/倶
丂偲偟偨曽偑屻偺揥奐偑妝偩偭偨偐傕偟傟側偄両傕偟偐偟偰丄弌戣幰偼丄庴尡惗偑偙偺傛偆
丂偵摫偔偙偲傪憐掕偟偰丄偦偺屻偺寁嶼偵偼偁傑傝柍撢拝偩偭偨偐傕丏丏丏丠
丂丂俥乭乮倶乯傪寁嶼偟偰傒傛偆丅
丂俥乫乮倶乯亖俀乮倶亄倎乯亄倐2乷俀倶乮倶亄倎乯亅俀乮倶亄倎乯2乸/倶3亅俀倐們倧倱兤乷俀乮倶亄倎乯倶亅乮倶亄倎乯2乸/倶2
丂丂丂丂丂亖俀乮倶亄倎乯亅倎倐2乮俀倶亄倎乯/倶3亅俀倐們倧倱兤乮倶2亅倎2乯/倶2
丂傛偭偰丄
丂俥乭乮倶乯亖俀亅倎倐2乷俀倶亅俁乮俀倶亄倎乯乸/倶4亅俀倎2倐們倧倱兤/倶3
丂丂丂丂丂亖俀亄倎倐2乮係倶亄俁倎乯/倶4亅俀倎2倐們倧倱兤/倶3
丂丂丂丂丂亖俀乷倶4亄俀倎倐2倶亅俀倎2倐倶們倧倱兤亄俁倎2倐2乸/倶4
偲偡傟偽丄屻偼丄杮夝偲摨條偵側傞丅乮側乣傞傎偳丏丏丏寁嶼偼偦傟傎偳戝曄偠傖側偄両乯
丂暯惉俀侾擭俁寧俈擔晅偗偱摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俽乮俫乯偝傫偑丄敾暿幃傪棙梡
偡傞夝朄傪採帵偝傟偨丅
丂丂俥乮倶乯亖乮倶4亄俁倶2亄侾侽倶亄俇乯/倶2亖倠丂偲偍偒丄暘曣傪暐偭偰惍棟偡傞偲丄
丂丂丂丂倶4亄乮俁亅倠乯倶2亄侾侽倶亄俇亖侽
丂偙偺敾暿幃偼丄俽乮俫乯偝傫偺寁嶼偵傛傟偽丄
丂丂丂俢亖侾俇倠乮俀倠亅俀俈乯乮俁倠2亄侾俈倠亄侾俁俆乯
偲側傞傜偟偄丅偙偺偙偲偐傜丄椪奅揰偼俀売強乮倠亖侽丂偲丂倠亖俀俈/俀乯偁傝丄婔壗妛揑偵峫偊
偰丄媮傔傞嵟彫抣偼丄倠亖俀俈/俀丂偺応崌偵梌偊傜傟傞偙偲偑暘偐傞丅
丂俽乮俫乯偝傫偺夝朄偵怗敪偝傟偰敾暿幃乮偲偄偆偐丏丏丏廳夝乯傪堄幆偟偨師偺夝朄傪巚偄偮
偄偨丅
丂丂丂丂俧乮倶乯亖倶4亄俁倶2亄侾侽倶亄俇丂丄丂俫乮倶乯亖倠倶2
偲偍偒丄俀偮偺嬋慄偑嫟捠愙慄傪帩偮応崌傪峫偊傟偽傛偄丅
丂丂丂丂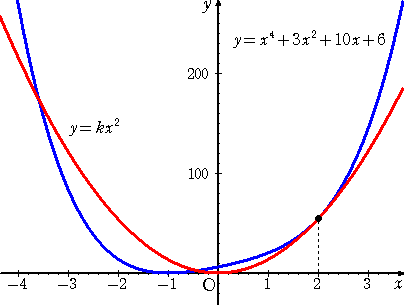
丂嫟捠愙慄偺愙揰偺 倶 嵗昗傪 倲 偲偍偔偲丄丂俧乮倲乯亖俫乮倲乯丂丄丂俧乫乮倲乯亖俫乫乮倲乯
丂丂丂偡側傢偪丄丂倲4亄俁倲2亄侾侽倲亄俇亖倠倲2丂丄丂係倲3亄俇倲亄侾侽亖俀倠倲
戞俀幃傛傝丄丂俀倲4亄俁倲2亄俆倲亖倠倲2丂側偺偱丄戞侾幃傪曈乆堷偔偲丄
丂丂丂丂丂丂倲4亅俆倲亅俇亖侽
丂場悢掕棟偵傛傝丄丂乮倲亄侾乯乮倲亅俀乯乮倲2亄倲亄俁乯亖侽丂側偺偱丄丂倲亖亅侾丄俀
丂倲亜侽丂偱偁傞偺偱丄倲亖亅侾丂偼晄揔
丂丂倲亖俀丂偺偲偒丄丂倠亖俀俈/俀
丂婔壗妛揑偵峫偊偰丄倠亖俀俈/俀丂偺偲偒丄俥乮倶乯亖乮倶4亄俁倶2亄侾侽倶亄俇乯/倶2丂偼嵟彫丅
乮僐儊儞僩乯丂忋婰偱偼丄暥帤 倠 傪徚嫀偟傑偟偨偑丄暥帤 倲 傪徚嫀偡傟偽敾暿幃偑摼傜傟傑
丂丂丂丂丂丂偡偹両
丂傑偨丄俽乮俫乯偝傫偵傛傟偽丄師偺傛偆側帇嵗傕壜擻偺傛偆偩丅
俛俻亖倷丂偲偍偔偲丄丂俷俻亖倐亄倎倐/倶亖倐乮倶亄倎乯/倶丂傛傝丄丂倐亄倷亖倐乮倶亄倎乯/倶
丂傛偭偰丄丂倐倶亄倶倷亖倐倶亄倎倐丂傛傝丄丂倶倷亖倎倐
偙偙偱丄丂倎亖侾丄倐亖![]() 丄們倧倱兤亖侾/
丄們倧倱兤亖侾/![]() 丂偲偡傟偽丄
丂偲偡傟偽丄
丂俧乮 倶 丆 倷 乯亖倶倷亅![]() 亖侽丂偺偲偒丄
亖侽丂偺偲偒丄
丂丂丂丂丂丂俥乮 倶 丆 倷 乯亖乮倶亄侾乯2亄乮倷亄![]() 乯2亅俀乮倶亄侾乯乮倷亄
乯2亅俀乮倶亄侾乯乮倷亄![]() 乯/
乯/![]()
偺嬌抣傪挷傋傟偽傛偄丅丂俥乮 倶 丆 倷 乯丂偺嬌抣傪梌偊傞揰乮 倱 丆 倲 乯偼師偺幃傪枮偨偡丅
丂丂丂丂丂丂丂丂丂丂俀乮倶亄侾乯亅俀乮倷亄![]() 乯/
乯/![]() 亄兩倷亖侽
亄兩倷亖侽
丂丂丂丂丂丂丂丂丂丂俀乮倷亄![]() 乯亅俀乮倶亄侾乯/
乯亅俀乮倶亄侾乯/![]() 亄兩倶亖侽
亄兩倶亖侽
丂丂丂丂丂丂丂丂丂丂丂丂丂倶倷亅![]() 亖侽
亖侽
偙偺偲偒丂俀乮倶亄侾乯倶亅俀倶乮倷亄![]() 乯/
乯/![]() 亄兩
亄兩![]() 亖侽丂傛傝丄
亖侽丂傛傝丄
丂丂俀![]() 乮倶亄侾乯倶亅俀倶乮倷亄
乮倶亄侾乯倶亅俀倶乮倷亄![]() 乯亄俇兩亖侽丂偡側傢偪丄丂俀
乯亄俇兩亖侽丂偡側傢偪丄丂俀![]() 倶2亅俀
倶2亅俀![]() 亄俇兩亖侽
亄俇兩亖侽
丂丂丂丂俀乮倷亄![]() 乯倷亅俀乮倶亄侾乯倷/
乯倷亅俀乮倶亄侾乯倷/![]() 亄兩
亄兩![]() 亖侽丂傛傝丄
亖侽丂傛傝丄
丂丂俀![]() 乮倷亄
乮倷亄![]() 乯倷亅俀乮倶亄侾乯倷亄俇兩亖侽丂偡側傢偪丄丂俀
乯倷亅俀乮倶亄侾乯倷亄俇兩亖侽丂偡側傢偪丄丂俀![]() 倷2亄侾侽倷亅俀
倷2亄侾侽倷亅俀![]() 亄俇兩亖侽
亄俇兩亖侽
傛傝丄曈乆堷偄偰丄丂俀![]() 乮倶2亅倷2乯亅侾侽倷亖侽丂偲側傞丅
乮倶2亅倷2乯亅侾侽倷亖侽丂偲側傞丅
丂偡側傢偪丄丂丂![]() 乮倶2亅倷2乯亅俆倷亖侽
乮倶2亅倷2乯亅俆倷亖侽
丂倷亖![]() /倶丂傪戙擖偟偰丄丂
/倶丂傪戙擖偟偰丄丂![]() 倶2亅俇
倶2亅俇![]() /倶2亅俆
/倶2亅俆![]() /倶亖侽丂傛傝丄丂倶4亅俆倶亅俇亖侽
/倶亖侽丂傛傝丄丂倶4亅俆倶亅俇亖侽
場悢暘夝偟偰丄丂乮倶亄侾乯乮倶亅俀乯乮倶2亄倶亄俁乯亖侽
丂倶亜侽丂偱偁傞偙偲偐傜丄丂倶亖俀丂偱丄偙偺偲偒丄丂倷亖![]() /俀
/俀
丂婔壗妛揑偵峫偊偰丄丂倶亖俀丂丄倷亖![]() /俀丂偺偲偒丄丂俥乮 倶 丆 倷 乯偼嬌彫偐偮嵟彫偲側傞丅
/俀丂偺偲偒丄丂俥乮 倶 丆 倷 乯偼嬌彫偐偮嵟彫偲側傞丅
丂丂丂丂丂丂丂丂丂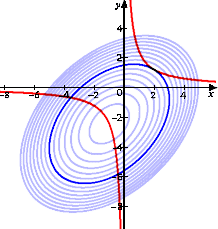
乮僐儊儞僩乯丂僷僜僐儞傪巊偆偲丄堦弖偱丄乽倶亖俀丂偵偍偄偰丄嬌彫偐偮嵟彫乿偑尒偊傑偡偹両