| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽俀侾 | 暯惉俀侾擭搙慜婜 | 墶昹崙棫戝妛 | 岺妛晹 | 丒丒丒 | 恾宍偲幃乮悢妛嘦乯 | 丂昗弨 |
丂偙偺栤戣偼丄恾宍偺抦幆丄夝愅婔壗偺抦幆偺椉柺偐傜傾僾儘乕僠偱偒丄椙栤偲巚偆丅
墶昹崙棫戝妛丂岺妛晹慜婜乮俀侽侽俋乯
丂倶倷 暯柺忋偵墌 俠 丗
倶2亄倷2亖侾丂偑偁傞丅俠 偺奜晹偺揰俹乮 倱 丆 倲 乯丂乮倱亗亇侾乯偐傜俠傊
堷偄偨俀偮偺愙慄偲捈慄
倶亖侾 偲偺岎揰傪俻丄俼 偲偡傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂慄暘俻俼偺挿偝傪 倱 丆 倲 傪梡偄偰昞偣丅
乮俀乯丂俻俼偺挿偝偑 侾
偱偁傞傛偆偵俹偑摦偔偲偒丄俹偺婳愓傪媮傔丄恾帵偣傛丅
乮夝乯乮侾乯丂嵗昗幉偺尨揰傪 俷
偲偡傞偲丄丂俷俹2亖倱2亄倲2丂偱偁傞丅
丂丂俀偮偺応崌偵暘偗偰峫偊傞丅
乮僀乯丂揰俹偑捈慄
倶亖侾 偺嵍懁偵偁傝丄倱亙亅侾 偺応崌
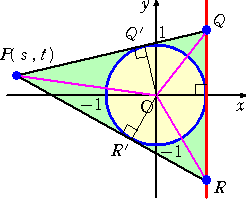 |
丂丂丂仮俹俻俼亖俻俼乮侾亅倱乯/俀 丂丂傑偨丄俹俻乫亖俹俼乫亖 丂丂丂仮俹俻俼亖 丂丂傛偭偰丄 丂丂丂俻俼乮侾亅倱乯亖俀 丂丂傛傝丄丂俻俼亖亅俀 |
乮儘乯丂揰俹偑捈慄 倶亖侾 偺嵍懁偵偁傝丄亅侾亙倱亙侾 偺応崌
丂丂丂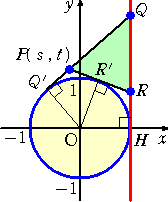 丂丂丂丂 丂丂丂丂 |
丂丂丂仮俹俻俼亖俻俼乮侾亅倱乯/俀 丂丂傑偨丄俹俻乫亖俹俼乫亖 丂丂丂巐妏宍俷俻乫俻俫亖俻俫丂傛傝丄 丂丂俻俼乮侾亅倱乯/俀亖俻俫亅 丂丂丂丂丂丂丂丂丂丂丂亖俻俼亅 丂丂傛傝丄丂俻俼亖俀 |
乮僴乯丂揰俹偑捈慄 倶亖侾 偺塃懁偵偁傞応崌
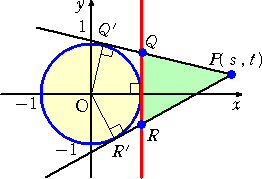 |
丂丂丂仮俹俻俼亖俻俼乮倱亅侾乯/俀 丂丂傑偨丄俹俻乫亖俹俼乫亖 丂丂丂巐妏宍俹俻乫俷俼乫亖 丂丂傛偭偰丄 丂丂丂俻俼乮倱亅侾乯亖俀 丂丂傛傝丄丂俻俼亖俀 |
丂埲忋偐傜丄俻俼偺幃傪傑偲傔傞偲丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]()
丂丂乮暿夝乯丂愙慄俹俻偺曽掱幃傪丄倷亖倣乮倶亅倱乯亄倲丂偲偍偔偲丄俻 偺倷
嵗昗亖倣乮侾亅倱乯亄倲
丂丂丂丂丂丂丂愙慄俹俼偺曽掱幃傪丄倷亖値乮倶亅倱乯亄倲丂偲偍偔偲丄俼 偺倷
嵗昗亖値乮侾亅倱乯亄倲
丂丂丂側偺偱丄丂俻俼亖乥乮倣亅値乯乮侾亅倱乯乥丂偲側傞丅
丂丂丂丂傑偨丄揰偲捈慄偺嫍棧偺岞幃傛傝丄
丂丂丂丂丂丂![]() 丂丂丂丄丂丂丂
丂丂丂丄丂丂丂![]()
丂丂丂傛偭偰丄丂倣2乮倱2亅侾乯亅俀倱倲倣亄倲2亅侾亖侽丂丄丂値2乮倱2亅侾乯亅俀倱倲値亄倲2亅侾亖侽
丂丂丂偙偺偙偲偐傜丄丂倣丄値丂偼俀師曽掱幃丂倶2乮倱2亅侾乯亅俀倱倲倶亄倲2亅侾亖侽丂偺夝側偺偱丄
丂丂丂夝偲學悢偺娭學偐傜丄丂倣亄値亖俀倱倲/乮倱2亅侾乯丂丄丂倣値亖乮倲2亅侾乯/乮倱2亅侾乯
丂丂丂偙偺偲偒丄丂乮倣亅値乯2亖乮倣亄値乯2亅係倣値
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖係倱2倲2/乮倱2亅侾乯2亅係乮倲2亅侾乯/乮倱2亅侾乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖係乮倱2亄倲2亅侾乯/乮倱2亅侾乯2
丂丂丂偙傟傪丄俻俼亖乥乮倣亅値乯乮侾亅倱乯乥丂偵戙擖偟偰惍棟偡傞偲丄
丂丂丂丂丂丂丂丂丂丂丂![]()
丂丂丂偲側傞丅
丂丂丂乮僐儊儞僩乯丂暿夝偺曽朄偵偼乽旤偟偝乿偑昚偭偰偄傑偡偹両偱傕丄偙偺夝朄傪帋尡応偱
丂丂丂丂丂丂丂丂丂巚偄偮偔偺偼戝曄偐側丠杮夝偱偼丄拞妛峑偺婔壗儗儀儖偱揇廘偔夝偄偰尒
丂丂丂丂丂丂丂丂丂傑偟偨両
乮俀乯丂俻俼亖侾丂側偺偱丄丂乮俀![]() 乯2亖乮倱亄侾乯2丂傛傝丄
乯2亖乮倱亄侾乯2丂傛傝丄
丂丂丂丂丂丂丂俁倱2亄係倲2亅俀倱亅俆亖侽
丂丂丂丂偙偙偱丄倱亖亇侾丂偺偲偒丄丂倲亖侽丄亇侾丂側偺偱丄
丂丂丂媮傔傞婳愓偺曽掱幃偼丄丂俁倶2亄係倷2亅俀倶亅俆亖侽
丂丂丂偨偩偟丄揰乮
侾 丆 侾 乯乮 侾 丆 亅侾 乯乮 亅侾 丆 侽 乯丂偼彍偐傟傞丅
丂丂丂丂丂丂丂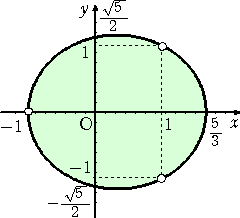
乮捛婰乯丂暯惉俀侾擭俁寧係擔晅偗
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俽乮俫乯偝傫偑丄忋婰偺栤戣傪師偺傛偆偵奼挘偝傟偨丅
丂倶倷 暯柺忋偵懭墌 俠 丗 倶2/倎2亄倷2/倐2亖侾丂乮 倎亜倐亜侽 乯偑偁傞丅
俠 偺奜晹偺揰俹乮 倱 丆 倲 乯丂乮倱亗亇倎乯偐傜俠傊堷偄偨俀偮偺愙慄偲捈慄
倶亖倎 偲偺岎揰傪俻丄
俼 偲偡傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂慄暘俻俼偺挿偝傪 倱 丆 倲 傪梡偄偰昞偣丅
乮俀乯丂俻俼偺挿偝偑 倓 偱偁傞傛偆偵俹偑摦偔偲偒丄俹偺婳愓傪媮傔丄恾帵偣傛丅
丂偙偙偱偼丄倎亖俀丄倐亖侾丄倓亖俀丂偲偟偰夝偄偰傒傛偆丅
乮夝乯丂乮侾乯丂愙慄俹俻偺曽掱幃傪丄倷亖倣乮倶亅倱乯亄倲丂偲偍偔偲丄俻
偺倷 嵗昗亖倣乮俀亅倱乯亄倲
丂丂丂丂愙慄俹俼偺曽掱幃傪丄倷亖値乮倶亅倱乯亄倲丂偲偍偔偲丄俼 偺倷 嵗昗亖値乮俀亅倱乯亄倲
丂丂丂側偺偱丄丂俻俼亖乥乮倣亅値乯乮俀亅倱乯乥丂偲側傞丅
丂丂丂丂傑偨丄捈慄偺曽掱幃丂倷亖倣乮倶亅倱乯亄倲丂傪懭墌偺曽掱幃丂倶2/係亄倷2亖侾丂偵戙擖偟
丂丂丂偰惍棟偡傞偲丄
丂丂丂丂丂丂丂乮係倣2亄侾乯倶2亄俉倣乮倲亅倣倱乯倶亄係乮倣2倱2亅俀倣倱倲亄倲2亅侾乯亖侽
丂丂丂愙偡傞忦審偐傜丄敾暿幃傪偲偭偰丄
丂丂丂丂丂丂丂侾俇倣2乮倲亅倣倱乯2亅係乮係倣2亄侾乯乮倣2倱2亅俀倣倱倲亄倲2亅侾乯亖侽
丂丂丂丂傛偭偰丄揥奐偟偰惍棟偡傞偲丄
丂丂丂丂丂丂丂乮係亅倱2乯倣2亄俀倣倱倲亅倲2亄侾亖侽
丂丂丂丂摨條偵偟偰丄丂乮係亅倱2乯値2亄俀値倱倲亅倲2亄侾亖侽
丂丂丂埲忋偐傜丄倣丄値 偼俀師曽掱幃丂乮係亅倱2乯倶2亄俀倱倲倶亅倲2亄侾亖侽丂偺夝偲側傞丅
丂丂丂夝偲學悢偺娭學偐傜丄丂倣亄値亖俀倱倲/乮倱2亅係乯丂丄丂倣値亖乮倲2亅侾乯/乮倱2亅係乯
丂丂丂偙偺偲偒丄丂乮倣亅値乯2亖乮倣亄値乯2亅係倣値
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖係倱2倲2/乮倱2亅係乯2亅係乮倲2亅侾乯/乮倱2亅係乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖係乮倱2亄係倲2亅係乯/乮倱2亅係乯2
丂丂丂偙傟傪丄俻俼亖乥乮倣亅値乯乮俀亅倱乯乥丂偵戙擖偟偰惍棟偡傞偲丄
丂丂丂丂丂丂丂丂丂丂丂![]()
丂丂丂偲側傞丅
乮俀乯丂俻俼亖俀丂偺偲偒丄丂倱2亄係倲2亅係亖乮倱亄俀乯2丂偐傜丄丂倲2亖倱亄俀丂側偺偱丄
丂丂丂媮傔傞婳愓偺曽掱幃偼丄丂倷2亖倶亄俀丂偲側傞丅
丂丂丂偨偩偟丄揰乮 亅俀 丆 侽 乯丂偼彍偐傟傞丅
丂丂丂丂丂
丂丂丂乮拲堄乯丂倶2亄係倷2亖係丂偵丄倷2亖倶亄俀丂傪戙擖偡傞偲丄丂倶2亄係倶亄係亖侽丂側偺偱丄
丂丂丂丂丂丂丂丂懭墌偲曻暔慄偼丄揰乮 亅俀 丆 侽 乯偺傒偱愙偟偰偄傞丅
乮僐儊儞僩乯丂墶崙偺栤戣偺応崌傕摨條偩偑丄忋恾偺揰乮 亅俀 丆 侽 乯偺嬤朤偺揰偵偍偗傞愙
丂丂丂丂丂丂慄偺條巕偑旝柇偱偡偹両偲丄俽乮俫乯偝傫偑巜揈偝傟偰偄傞丅
丂丂丂丂丂丂丂懭墌偵愙偡傞俀愙慄傪昤偄偨偲偒偵丄梱偐斵曽偱捈慄 倶亖俀 傪愗傝偲傞慄暘偺
丂丂丂丂丂丂挿偝偑 俀 偵側偭偰偄傞條傪摢偱偼棟夝偱偒偰傕丄幚嵺偵恾帵偡傞偲側傞偲帄擄偺
丂丂丂丂丂丂媄偐側丏丏丏丠
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俽乮俫乯偝傫偑丄偝傜偵丄師偺傛偆偵奼挘偝傟偨丅
丂倶倷 暯柺忋偵懭墌 俠 丗 倶2/倎2亄倷2/倐2亖侾丂乮 倎亜倐亜侽 乯偑偁傞丅
俠 偺奜晹偺揰俹乮 倱 丆 倲 乯丂乮倱亗亇倎乯偐傜俠傊堷偄偨俀偮偺愙慄偲捈慄
倶亖倣 偲偺岎揰傪俻丄
俼 偲偡傞丅師偺栤偄偵摎偊傛丅
乮侾乯丂慄暘俻俼偺挿偝傪 倱 丆 倲 丆 倣 傪梡偄偰昞偣丅
乮俀乯丂俻俼偺挿偝偑 倓 偱偁傞傛偆偵俹偑摦偔偲偒丄俹偺婳愓傪媮傔丄恾帵偣傛丅
丂忋婰偱丄丂倎亖侾丂丄倐亖侾丂偲摿庩壔偟丄
丂丂丂(僀)丂倣亖俀丂丄倓亖俈
丂丂丂(儘)丂倣亖俁丂丄倓亖俆
側偳偲丄倣丄倓 偺抣傪偄傠偄傠曄偊偰丄俹偑摦偔偲偒偺俹偺婳愓傪媮傔偰傒傞偙偲傕柺敀偄偺
偱偼丠偲丄俽乮俫乯偝傫偑嬄偭偰偄傞丅