丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
| 侽侾俋 |
暯惉俀侾擭搙慜婜 |
墶昹崙棫戝妛 |
岺妛晹 |
丒丒丒 |
旝暘愊暘乮悢妛嘨乯 |
丂昗弨 |
丂墶昹崙棫戝妛擖帋栤戣偺摿挜偼丄偙傟偱傕偐偲偄偆偔傜偄偵寁嶼検偵埑搢偝傟傞偙偲偩傠
偆丅偟偨偑偭偰丄尒捠偟傪帩偭偰寁嶼偟側偄偲惵栘儢尨庽奀傪渇渞偆怱嫬偵側傞偙偲昁掕偱偁
傞丅
墶昹崙棫戝妛丂岺妛晹慜婜乮俀侽侽俋乯
丂倶倷 暯柺忋偵嬋慄 俠 丗
倷亖倶2丂偑偁傞丅俠 忋偺揰俹乮 倲 丆 倲2
乯傪師偺忦審(*)傪枮偨偡傛偆
偵偲傞丅
(*)丂俹埲奜偺俠忋偺堎側傞俀揰俻丄俼偑偁傝丄偦偙偱偺俠偺朄慄偑偲傕偵俹傪捠傞
俻乮
兛 丆 兛2 乯丄俼乮 兝 丆 兝2 乯丂乮兛亙兝乯偲偡傞偲偒丄師偺栤偄偵摎偊傛丅
| 乮侾乯丂倲 偺偲傝偆傞抣偺斖埻傪媮傔傛丅 |
| 乮俀乯丂倲
偑乮侾乯偱媮傔偨斖埻傪摦偔偲偒丄慄暘俻俼偺拞揰俵偑昤偔婳愓偺曽掱幃傪媮傔傛丅 |
| 乮俁乯丂兝 傪 倲 偺幃偱昞偟丄嬌尷 |
丂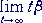 |
丂傪媮傔傛丅 |
乮夝乯乮侾乯丂倷乫亖俀倶丂傛傝丄揰俻偵偍偗傞朄慄偺曽掱幃偼丄
丂丂丂丂倷亖亅乷侾/乮俀兛乯乸乮倶亅兛乯亄兛2亖亅乷侾/乮俀兛乯乸倶亄兛2亄侾/俀
丂丂丂丂偙偺朄慄偼丄揰俹傪捠傞偺偱丄丂倲2亖亅乷侾/乮俀兛乯乸倲亄兛2亄侾/俀
丂丂摨條偵偟偰丄揰俼偱偺朄慄偺曽掱幃傪峫偊偰丄丂倲2亖亅乷侾/乮俀兝乯乸倲亄兝2亄侾/俀
丂傛偭偰丄兛
丄兝
偼曽掱幃丂倲2亖亅乷侾/乮俀倶乯乸倲亄倶2亄侾/俀丂偺堎側傞俀偮偺幚悢夝偱偁傞丅
丂暘曣傪暐偭偰惍棟偡傞偲丄丂俀倶3亄乮侾亅俀倲2乯倶亅倲亖侽
丂偙偺俁師曽掱幃偼場悢暘夝偝傟偰丄丂乮倶亅倲乯乮俀倶2亄俀倲倶亄侾乯亖侽
丂俻丄俼偼俹偲堎側傞揰偱偁傞偺偱丄兛
丄兝
偼曽掱幃丂俀倶2亄俀倲倶亄侾亖侽丂偺堎側傞俀偮偺
幚悢夝偱偁傞丅傛偭偰丄敾暿幃傪俢偲偡傞偲丄
丂丂丂俢/係亖倲2亅俀亜侽丂傛傝丄丂倲亙亅 丂丄丂
丂丄丂 亙倲
亙倲
丂丂丂乮暿夝乯丂俠忋偺揰乮 倱 丆 倱2 乯偲揰俹傪寢傇慄暘偺孹偒偼丄丂倱亄倲
丂丂丂丂丂傑偨丄揰乮 倱 丆 倱2 乯偵偍偗傞愙慄偺孹偒偼丄丂俀倱
丂丂丂丂傛偭偰丄偙傟傜俀偮偺慄暘偼悅捈側偺偱丄丂俀倱乮倱亄倲乯亖亅侾
丂丂丂丂丂丂偡側傢偪丄丂俀倱2亄俀倱倲亄侾亖侽
丂丂丂丂偙偺偲偒丄俀師曽掱幃 俀倶2亄俀倲倶亄侾亖侽丂偼堎側傞俀偮偺幚悢夝 兛丄兝 傪帩偮偺偱丄
丂丂丂丂敾暿幃傪俢偲偡傞偲丄丂俢/係亖倲2亅俀亜侽丂傛傝丄丂倲亙亅 丂丄丂
丂丄丂 亙倲丂乮暿夝廔乯
亙倲丂乮暿夝廔乯
乮俀乯丂俀倶2亄俀倲倶亄侾亖侽丂偵偍偄偰丄夝偲學悢偺娭學偐傜丄
丂丂丂丂丂丂兛亄兝亖亅倲丂丄丂兛兝亖侾/俀
丂丂俵乮
倶 丆 倷
乯偲偍偔偲丄丂倶亖乮兛亄兝乯/俀亖亅倲/俀丂傛傝丄丂倲亖亅俀倶
丂丂倷亖乮兛2亄兝2乯/俀亖乷乮兛亄兝乯2亅俀兛兝乸/俀亖乮倲2亅侾乯/俀亖乮係倶2亅侾乯/俀
丂丂偡側傢偪丄婳愓偺曽掱幃偼丄丂倷亖乮係倶2亅侾乯/俀丂乮倶亙亅侾/ 丂丄丂倲亜侾/
丂丄丂倲亜侾/ 乯
乯
乮俁乯丂倲兝亖亅乮俀兝2亄侾乯/俀丂偵偍偄偰丄丂倲丂仺丂亣丂偺偲偒丄兝丂仺丂侽丂側偺偱丄
丂丂丂倲兝丂仺丂亅侾/俀丂偱偁傞丅
乮僐儊儞僩乯丂俀倶3亄乮侾亅俀倲2乯倶亅倲亖侽丂偑場悢暘夝偱偒傞偙偲偵嵟弶婥偑偮偐側偔偰丄俁師娭
丂丂丂丂丂丂悢偺嬌抣偺愊偑堎晞崋偐傜
倲
偺斖埻傪媮傔傑偟偨丅偨偩丄寁嶼搑拞偱嬼慠偵場
丂丂丂丂丂丂悢暘夝偱偒傞偙偲偑暘偐傝丄偦傟傑偱偺寁嶼検偺懡偝偵鐒堈偟偰偄偨偲偙傠側偺偱丄
丂丂丂丂丂丂壗偲側偔媬傢傟偨婥帩偪偵側傝傑偟偨両偙傫側栤戣傪弌戣偝傟偨墶崙偺愭惗偼怱
丂丂丂丂丂丂憺偄偱偡偹丏丏丏丅
![]() 丂丄丂
丂丄丂![]() 亙倲
亙倲![]() 丂丄丂
丂丄丂![]() 亙倲丂乮暿夝廔乯
亙倲丂乮暿夝廔乯![]() 丂丄丂倲亜侾/
丂丄丂倲亜侾/![]() 乯
乯