０１８	平成２１年度前期	東京工業大学	理系	・・・	回転体の体積（数学�V）	標準

　中学・高校を含めて学校現場からは、空間に関する指導が以前ほど熱心に行われなくな
りつつある。現実問題として、学習指導要領から空間に関する扱いは軽減する方向で動い
ている。

　それにも拘わらず、東京工業大学がこのような空間把握を要する入試問題を出題すると
いうことは、出題者が高校生の学力レベルの実状を全く知らないか、または、これくらいの
空間把握と計算力は身につけてきてね！という大学側のメッセージの何れかだろう。

　今年の問題は比較的取り組みやすい問題が多かった中で、最後の第４問は、大きな壁
となって受験生の前に立ちはだかり、受験生も苦戦したことだろう。

　ただ、予備校では必ず教えられる問題なので、経験の有無が得点に大きく響くことになる
ものと推察される。


東京工業大学　理系（２００９）

　ｘｙｚ空間の原点と点（ １ ， １ ， １ ）を通る直線を Ｌ とする。
（１）　Ｌ 上の点（ ｔ/３ ， ｔ/３ ， ｔ/３ ）を通り、Ｌ と垂直な平面が ｘｙ 平面と交わってできる直
　　　線の方程式を求めよ。
（２）　不等式 ０≦ｙ≦ｘ（１−ｘ）　の表す ｘｙ 平面内の領域を Ｄ とする。Ｌを軸としてＤを回転
　　　させて得られる回転体の体積を求めよ。


　この問題では、回転体の切断面がどのような形状になるかを考えることがポイントになる
だろう。

（解）　（１）　Ｌ 上の点（ ｔ/３ ， ｔ/３ ， ｔ/３ ）を通り、Ｌ と垂直な平面の方程式は、

　　　　　　　　　（ｘ−ｔ/３）＋（ｙ−ｔ/３）＋（ｚ−ｔ/３）＝０　　すなわち、　ｘ＋ｙ＋ｚ＝ｔ

　　　　　　　よって、ｘｙ 平面との交線の方程式は、　ｚ＝０　として、

　　　　　　　　　　ｘ＋ｙ＝ｔ　、　ｚ＝０

（２）　領域 Ｄ と（１）で求めた直線の方程式の関係を図示すると左下図のようになる。

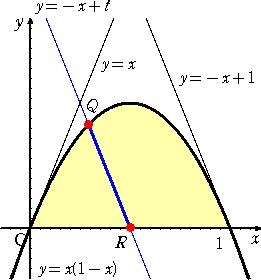　　Ｐ（ ｔ/３ ， ｔ/３ ， ｔ/３ ）とすると、

　　　Ｑ（ α ， ｔ−α ， ０ ）

　　　　　ただし、　α＝

　　　Ｒ（ ｔ ， ０ ， ０ ）

　　である。

　　　回転体を、点Ｐを通り直線Ｌに垂直な平面で

　　切った切り口は下図のような図形となる。





　　　　　　　　　

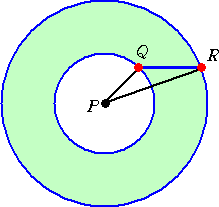
　このとき、　断面積 Ｓ＝π（ＰＲ²−ＰＱ²）＝π（２ｔα−２α²）　となる。

　ＯＰ＝ｘ　とすると、　ｘ²＝ｔ²/３　より、　ｘ＝ｔ/　なので、　ｄｘ＝ｄｔ/

　求める回転体の体積をＶとおくと、

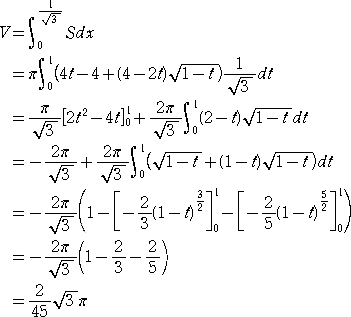　　　（終）