| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽侾俈 | 暯惉俀侾擭搙慜婜 | 搶嫗岺嬈戝妛 | 棟宯 | 丒丒丒 | 惍悢栤戣乮悢妛嘦乯 | 丂昗弨 |
丂搶嫗岺嬈戝妛偺擖帋栤戣偲尵偊偽丄惍悢栤戣偑昿弌偲偄偆偙偲偱丄崱擭搙傕弌戣偝傟偨丅
丂崱擭偺栤戣偼旘傃偒傝偵擄偟偄儗儀儖偱偼側偔丄崅峑悢妛偱妛傫偩偙偲傪嬱巊偡傟偽扤偱
傕偑惓夝偵払偡傞椙幆揑側椙栤偱偁偭偨丅
搶嫗岺嬈戝妛丂棟宯乮俀侽侽俋乯
丂俶傪惓偺惍悢偲偡傞丅俀俶埲壓偺惓偺惍悢 倣 丄値 偐傜側傞慻乮 倣 丆 値 乯偱
曽掱幃 倶2亅値倶亄倣亖侽 偑俶埲忋偺幚悢夝傪帩偮傛偆側傕偺偼壗屄偁傞偐丅
丂偙偺栤戣偱偼丄夝偺暘棧栤戣丄椞堟偺抦幆偑栤傢傟丄傑偢壗傪媮傔傞偺偐傪恾帵偡傞
偙偲偑億僀儞僩偵側傞偩傠偆丅
乮夝乯丂俥乮倶乯亖倶2亅値倶亄倣丂偲偍偔丅丂幉偺曽掱幃偼丄丂倶亖値/俀丂偱丄丂値亝俀俶丂傛傝丄
丂丂丂倶亖値/俀亝俶丂偱偁傞丅
丂丂傛偭偰丄曽掱幃 倶2亅値倶亄倣亖侽丂偑俶埲忋偺幚悢夝傪帩偮偨傔偺昁梫廫暘忦審偼丄
丂丂丂俥乮俶乯亝侽丂偡側傢偪丄丂俶2亅値俶亄倣亝侽丂偱偁傞丅
丂丂乮僀乯丂俶亖侾丂偺偲偒丄丂倣亝値亅侾丂丄侾亝倣亝俀丂丄侾亝値亝俀丂傪枮偨偡惓偺惍悢偺慻
丂丂丂丂乮 倣 丆 値 乯偺屄悢傪挷傋傟偽傛偄丅
丂丂丂丂忦審傪枮偨偡慻偼丄乮 倣 丆 値 乯亖乮 侾 丆 俀 乯丂偺侾慻偺傒偱偁傞丅
丂丂乮儘乯丂俶亞俀丂偺偲偒丄丂倣亝俶丒値亅俶2丂丄侾亝倣亝俀俶丂丄侾亝値亝俀俶丂傪枮偨偡惓偺惍
丂丂丂丂悢偺慻乮 倣 丆 値 乯偺屄悢傪挷傋傟偽傛偄丅
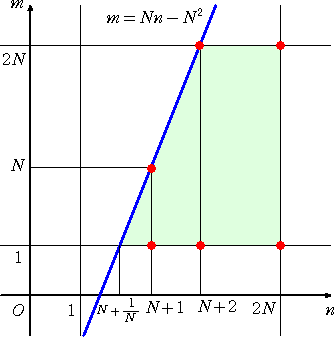 丂丂嵍恾偵偍偄偰丄忦審傪枮偨偡慻偺
丂丂嵍恾偵偍偄偰丄忦審傪枮偨偡慻偺
丂屄悢偼丄
丂丂俶亄俀俶亄俀俶乷俀俶亅乮俶亄俀乯乸
丂亖俀俶2亅俶
丂偱偁傞丅
丂偙偺幃偼丄俶亖侾偺偲偒傕惉傝棫偮丅
丂偟偨偑偭偰丄媮傔傞屄悢偼丄
丂丂丂丂俀俶2亅俶丂乮屄乯
丂偱偁傞丅丂乮廔乯
乮僐儊儞僩乯丂暯惉俀侾擭俀寧俀俉擔尰嵼偱丄壨崌弇丄戙僛儈偼傑偩偙偺栤戣偺夝摎傪岞昞偟偰
丂丂丂丂丂丂偄側偄偑丄弜戜偵愭傪墇偝傟偰偟傑偭偨丅嶐擔夝摎傪傾僢僾偡傋偒偱偁偭偨偲屻夨両
丂栤戣暥偱偼惍悢偺慻乮 倣 丆 値 乯偲側偭偰偄傞偑丄幚嵺偵悢偊傞偺偼惍悢偺慻乮
値 丆 倣 乯
偺曽丅偙偺曽偑娙寜偵悢偊傜傟傞丅弜戜偺曽傕偦偺傛偆偵尵媦偝傟偰偄傞丅
丂惍悢偺慻乮 値 丆 倣 乯偲偡傋偒偲偙傠傪丄惍悢偺慻乮 倣 丆 値 乯偲偟偨偺偼弌戣幰偺僀僕儚儖
偐丄偼偨傑偨丄乽偦傟偖傜偄婥偑偮偗儓両乿偲偄偆幎欱寖椼側偺偩傠偆偐丠