０１６	平成２１年度	慶應義塾大学	理工	・・・	確率と漸化式（数学�V）	標準

　そろそろ平成２１年度私立大学の天王山が終わろうとしている。塾生からとってもホットな
入試問題が入手できたので、どこの予備校よりもいち早く解答を公開したいと思う。

　理工学部は、５題１２０分で解かなければならないが、真面目に計算をしようとすると大変
な計算量になる。空欄補充形式にしているのは、大学側の若干の親心なのだろう。

　第１問　（１）三角関数の半角の公式または加法定理を用いる問題（数学�T・�U）
　　　　　　（２）面積計算と、接点、垂線の足を求める問題（数学�U）
　　　　　　（３）回転体の体積の問題（数学�V）
　第２問　確率と漸化式、期待値を無限級数から求めさせる問題（数学�V・Ａ・Ｂ）
　第３問　円と双曲線が接する場合を考えさせる問題（数学�U・Ｃ）
　第４問　３次方程式の整数解の個数とその極限値に関する問題（数学�U・�V）
　第５問　円から円、直線から直線に移る１次変換を求めさせる問題（数学Ｃ）

　このページでは、私自身が最も興味を持った第２問について考えたいと思う。


慶應義塾大学　理工（２００９）

　さいころを投げるという試行を繰り返し行う。ただし、２回以上連続して５以上の目が出た
場合は、それ以降の試行は行わないものとする。

　ｎ 回目の試行が行われ、かつ、ｎ 回目に出た目が４以下になる確率を ｐ_ｎ とする。この
とき、ｐ₁＝２/３　、ｐ₂＝（　　　　） 、ｐ₃＝（　　　　） である。また、ｐ₀＝１　とおく。

　ｎ ≧０ に対して、ｐ_ｎ 、ｐ_ｎ+1 、ｐ_ｎ+2 の間に成立する関係式を求め、それを

　　　　　ｐ_ｎ+2−βｐ_ｎ+1＝α（ｐ_ｎ+1−βｐ_ｎ）　　（α＞β）

の形に書くと、α＝（　　　　） である。よって、ｐ_ｎ＝/２（　　　　） となる。

　また、ｎ 回目の試行が行われ、かつ、ｎ 回目に出た目が５以上になる確率を ｑ_ｎ とする。
このとき、 ｑ_１＝１/３　である。

　ｎ≧２ とするとき、ｑ_ｎ と ｐ_ｎ-1 、ｐ_ｎ-2 の間には、ｑ_ｎ＝（　　　　）なる関係式が成り立つ。

したがって、５以上の目が出る回数の期待値は、

　　　　　

である。


　この問題では、「２回以上連続して５以上の目が出た場合は、それ以降の試行は行わな
い」という条件を適切に使えるかどうかがポイントになるだろう。

（解）

　同様にして、ｐ_ｎ 、ｐ_ｎ+1 、ｐ_ｎ+2 の間に成立する関係式を考える。２回以上連続して５以上

の目が出た場合は、それ以降の試行は行わないので、起こりうる場合は下表のようになる。

　このとき、特性方程式は、　ｘ²−（2/3）ｘ−（2/9）＝０　すなわち、　９ｘ²−６ｘ−２＝０

　これを解いて、
　　　　　　　　　　　　、　

　このとき、　漸化式　ｐ_ｎ+2−（2/3）ｐ_ｎ+1−（2/9）ｐ_ｎ＝０　は、

　　　　　　　　　　ｐ_ｎ+2−βｐ_ｎ+1＝α（ｐ_ｎ+1−βｐ_ｎ）

と書ける。　よって、　ｐ_ｎ+1−βｐ_ｎ＝α^ｎ（ｐ₁−βｐ₀）

　ここで、　ｐ₁−βｐ₀＝２/３−β＝α　なので、　ｐ_ｎ+1−βｐ_ｎ＝α^ｎ+1

　同様にして、　ｐ_ｎ+2−αｐ_ｎ+1＝β（ｐ_ｎ+1−αｐ_ｎ）　、　ｐ₁−αｐ₀＝β　より、

　　　　　　　ｐ_ｎ+1−αｐ_ｎ＝β^ｎ+1

　したがって、２式を辺々引いて、　（α−β）ｐ_ｎ＝α^ｎ+1−β^ｎ+1

　ここで、　α−β＝２/３＝２/　より、　ｐ_ｎ＝（/２）（α^ｎ+1−β^ｎ+1）　となる。

　次に、ｑ_ｎ 、ｐ_ｎ-1 、ｐ_ｎ-2 の間に成立する関係式を考える。この場合も、２回以上連続して

５以上の目が出た場合は、それ以降の試行は行わないという条件が決定的な役割を果た

す。　ｎ ≧２　のとき、起こりうる場合は下表のようになる。

　上表より、　ｑ_ｎ ＝ｐ_ｎ-1×（1/3）＋ｐ_ｎ-2×（1/3）（1/3）＝（1/3）ｐ_ｎ-1＋（1/9）ｐ_ｎ-2

　したがって、５以上の目が出る回数の期待値は、　−１＜α、β＜１　に注意して、

　　　

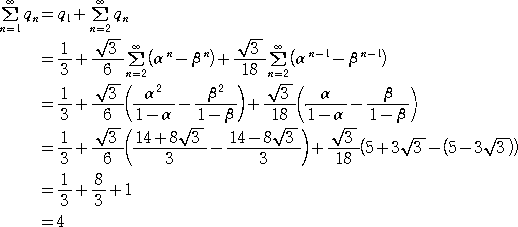
　となる。　　（終）

（コメント）　確率というのは出だしだけで、ほとんど数学�V・数学Ｂの問題ですね！定められ
　　　　　　た時間内に完答するのは大変な問題だと思います。正直に告白すると、「２回以上
　　　　　　連続して５以上の目が出た場合は、それ以降の試行は行わない」という条件を巧
　　　　　　妙に使い回して漸化式を得るのに結構時間を費やしました．．．　ｆ(^^;)