| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽侾俀 | 暯惉俀侽擭搙慜婜 | 嬨廈戝妛 | 棟宯 | 丒丒丒 | 嶰妏娭悢乮悢妛嘦乯 | 丂昗弨 |
丂梊旛峑偺敾抐偱偼丄乽傗傗擄乿偵懏偡傞栤戣傜偟偄偑丄撪梕揑偵偼嫵壢彂偺復枛栤戣儗
儀儖偱斾妑揑椙栤偺斖醗偵擖傞栤戣偩傠偆丅
丂捈姶揑偵偼摎偊偑椶悇偱偒傞偑丄偒偭偪傝榑弎偡傞偵偼尰栶偺崅峑惗偵偼尩偟偄偐傕偟
傟側偄丅偦偺堄枴傪崬傔偰丄乽傗傗擄乿側偺偐側丠
嬨廈戝妛丂棟宯乮俀侽侽俉乯
丂偄偔偮偐偺敿宎俁偺墌傪丄敿宎俀偺墌俻偵奜愙偟丄偐偮丄屳偄偵岎傢傜側偄傛偆偵攝抲偡
傞丅偙偺偲偒丄師偺栤偄偵摎偊傛丅
乮侾乯丂敿宎俁偺墌偺侾偮傪俼偲偡傞丅墌俻偺拞怱傪抂揰偲偟丄墌俼偵愙偡傞俀杮偺敿捈慄偺
丂丂丂側偡妏傪兤偲偍偔丅偨偩偟丄侽亙兤亙兾偲偡傞丅偙偺偲偒丄倱倝値兤傪媮傔傛丅
乮俀乯丂兾/俁亙兤亙兾/俀丂傪帵偣丅
乮俁乯丂攝抲偱偒傞敿宎俁偺墌偺嵟戝屄悢傪媮傔傛丅
丂挿偝偺巜掕偑偁傞偺偱丄偦傟偵拤幚偵廬偭偰嶌恾偡傞偲丄壓恾偺傛偆偵側傞丅
丂丂丂丂丂丂丂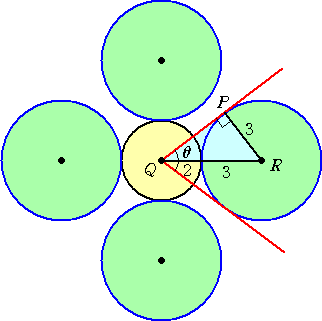
丂忋恾偐傜丄兾/俁亙兤亙兾/俀丂偱偁傞偙偲偼廫暘梊憐偝傟傞偟丄攝抲偱偒傞墌偺嵟戝屄悢
傕係屄偱偁傞偙偲偑弖帪偵椆夝偝傟傞偙偲偩傠偆丅
丂傗偼傝丄悢妛偼栤戣偺堄枴偡傞偙偲傪奊偵偡傞偲丄敿偽夝偗偨傕摨慠偱偡偹両
乮夝乯丂乮侾乯丂倱倝値乮兤/俀乯亖俁/俆丂側偺偱丄丂們倧倱乮兤/俀乯亖係/俆
丂丂丂丂丂丂丂傛偭偰丄丂倱倝値兤亖俀倱倝値乮兤/俀乯們倧倱乮兤/俀乯亖俀係/俀俆
丂丂丂丂乮俀乯丂們倧倱兤亖俀們倧倱2乮兤/俀乯亅侾亖俈/俀俆丂偱丄丂侽亙們倧倱兤亙侾/俀丂傛傝丄
丂丂丂丂丂丂丂兾/俁亙兤亙兾/俀丂偑惉傝棫偮丅
丂丂丂丂乮俁乯丂兛亖俀兾/俆丂偲偍偔偲丄丂俆兛亖俀兾丂側偺偱丄丂俁兛亖俀兾亅俀兛
丂丂丂丂丂丂丂傛偭偰丄丂倱倝値俁兛亖倱倝値乮俀兾亅俀兛乯亖亅倱倝値俀兛丂偵偍偄偰丄
丂丂丂丂丂丂丂俀攞妏偺岞幃偍傛傃俁攞妏偺岞幃傛傝丄
丂丂丂丂丂丂丂丂丂丂俁倱倝値兛亅係倱倝値3兛亖亅俀倱倝値兛們倧倱兛
丂丂丂丂丂丂丂倱倝値兛亗侽丂側偺偱丄丂俁亅係倱倝値2兛亖亅俀們倧倱兛
丂丂丂丂丂丂丂倱倝値2兛亖侾亅們倧倱2兛丂側偺偱丄丂係們倧倱2兛亄俀們倧倱兛亅侾亖侽
丂丂丂丂丂丂丂丂傛偭偰丄丂丂係們倧倱兛亖亅侾亇![]() 丂偱偁傞偑丄們倧倱兛亜侽丂側偺偱丄
丂偱偁傞偑丄們倧倱兛亜侽丂側偺偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂係們倧倱兛亖亅侾亄![]()
丂丂丂丂丂丂丂丂丂丂丂係亊乮俈/俀俆乯亄侾亖俆俁/俀俆亙俆俆/俀俆亖侾侾/俆
丂丂丂丂丂丂丂丂丂丂乮侾侾/俆乯2亖侾俀侾/俀俆亙俆丂側偺偱丄丂侾侾/俆亙![]()
丂丂丂丂丂丂丂丂偡側傢偪丄丂丂丂係亊乮俈/俀俆乯亄侾亙![]() 丂傛傝丄丂們倧倱兤亙們倧倱兛
丂傛傝丄丂們倧倱兤亙們倧倱兛
丂丂丂丂丂丂丂丂丂偟偨偑偭偰丄丂兤亜俀兾/俆丂傛傝丄丂俆兤亜俀兾
丂丂丂丂丂丂丂丂埲忋偐傜丄攝抲偱偒傞墌偺嵟戝屄悢偼丄係屄偱偁傞丅丂乮廔乯
乮僐儊儞僩乯丂乮俁乯偼丄乮俀乯偵偍偗傞兤偺昡壙偑娒偐偭偨両偲偄偆弌戣幰偺斀徣偐傜惗傑傟偨
丂丂丂丂丂丂傕偺偩傠偆丅兾/俁亙兤亙兾/俀丂偐傜攝抲偱偒傞墌偺嵟戝屄悢偼丄柧傜偐偵
係屄
丂丂丂丂丂丂傑偨偼 俆屄 偱偁傞偑丄偦偙傪傕偆彮偟徻偟偔嬦枴偟偰梸偟偄偲偄偆栤戣偱偁傞丅
丂丂丂丂丂丂丂俆兤偑俀兾傪挻偊傞偐偳偆偐傪敾抐偡傟偽傛偄偺偱丄忋婰偺傛偆側夝摎偑帺慠
丂丂丂丂丂丂偵摫偐傟傞丅