| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
||||||
| 侽侽俉 | 暯惉侾俋擭搙慜婜 | 搶嫗戝妛 | 棟宯 | 丒丒丒 | 旝暘愊暘乮悢妛嘨乯 | 丂傗傗擄 |
丂搶嫗戝妛偺栤戣偱丄偙傟傎偳乽慺捈丠乿側栤戣傪崱傑偱尒偨偙偲偑側偄丅恾宍傪堄幆偡傟
偽丄梕堈偵夝朄偑摫偗傞偩傠偆丅庴尡惗儗儀儖偐傜尒偰乽傗傗擄乿偲偄偆偙偲偩偑丄傕偟偐偟
偨傜丄栤戣儗儀儖偼堦愄慜偲斾傋偰乽堈乿偐傕偟傟側偄丅
丂屄恖揑偵偼丄乮俀乯偺傛偆側栤戣偵怱堷偐傟傞丅
搶嫗戝妛丂棟宯乮俀侽侽俈乯
丂埲壓偺栤偄偵摎偊傛丅
乮侾乯丂侽亙倶亙倎 傪傒偨偡幚悢 倶 丄 倎 偵懳偟丄師傪帵偣丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]()
乮俀乯丂乮侾乯傪棙梡偟偰丄師傪帵偣丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂侽丏俇俉亙倢倧倗俀亙侽丏俈侾
丂丂丂偨偩偟丄倢倧倗俀 偼丄俀 偺帺慠懳悢傪昞偡丅
乮夝乯乮侾乯丂丂侽亙倎亅倶亙倎亄倶丂側偺偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]() 丂
丂
丂丂丂丂丂丂偼丄壓恾偺墿怓偄晹暘偺柺愊偱偁傞丅
丂丂丂丂丂丂丂丂丂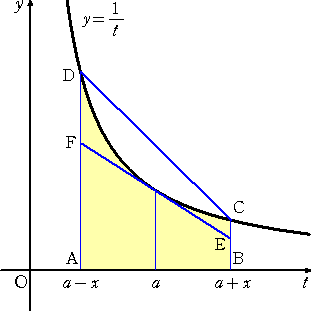
丂丂傑偨丄揰乮 倎 丆 侾/倎 乯偵偍偗傞愙慄偺曽掱幃偼丄丂倷亖乮俀倎亅倲乯/倎2丂偱丄
丂丂丂倲亖倎亅倶丂偺偲偒丄丂倷亖乮倎亄倶乯/倎2亜侽
丂丂丂倲亖倎亄倶丂偺偲偒丄丂倷亖乮倎亅倶乯/倎2亜侽
丂埲忋偐傜丄俀揰 俤 丄 俥 偼戞侾徾尷偵偁傞丅
丂丂偙偺偲偒丄恾偐傜柧傜偐偵丄
| 丂丂丂丂丂丂丂丂丂丂丂戜宍俙俛俤俥偺柺愊 | 亙 | 亙 | 戜宍俙俛俠俢偺柺愊 |
丂丂丂偙偙偱丄丂戜宍俙俛俤俥偺柺愊亖俀倶丒乮侾/倎乯亖俀倶/倎
丂丂丂丂丂丂丂丂丂戜宍俙俛俠俢偺柺愊亖乮侾/乮倎亄倶乯亄侾/乮倎亅倶乯乯丒俀倶丒乮侾/俀乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖倶乮侾/乮倎亄倶乯亄侾/乮倎亅倶乯乯
丂丂丂埲忋偐傜丄乮侾乯偺晄摍幃偼惉傝棫偮丅
乮俀乯丂
丂丂丂丂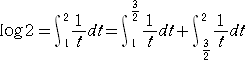
丂丂丂偱偁傞偙偲偵拲堄偟偰丄丂乮侾乯傛傝丄
丂丂丂丂丂丂丂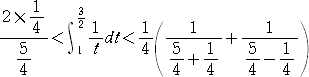
丂丂丂丂丂丂丂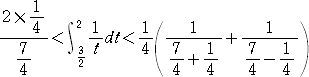
丂丂丂傛偭偰丄曈乆壛偊偰丄丂丂丂丂侽丏俇俉俆俈丒丒丒亙倢倧倗俀亙侽丏俈侽俉俁丒丒丒
丂丂偡側傢偪丄丂丂丂侽丏俇俉亙倢倧倗俀亙侽丏俈侾丂丂丂丂偑惉傝棫偮丅丂丂乮廔乯