Ｊｏｒｄａｎの不等式 　　　　　　　　　　　　　　　　　　　　　　　　　

　次の不等式

のとき、

は、Ｊｏｒｄａｎの不等式（Ｊｏｒｄａｎ’ｓ　ｉｎｅｑｕａｌｉｔｙ）と言われる。

　この不等式は、図を書けば直感的に了解されるだろう。


　　　　　　

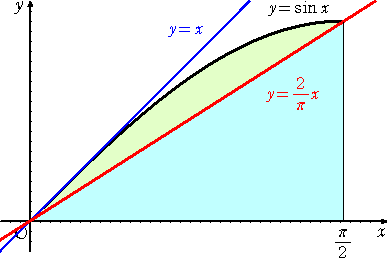
解析学的には、次のように証明されるのだろう。

（証明）　ｙ＝ｓｉｎ ｘ　とおくと、その第２次導関数は、　ｙ”＝−ｓｉｎ ｘ　であることから、
　　　　０≦ｘ≦π/２　において、　ｙ”≦０　である。
　　　　　よって、　０≦ｘ≦π/２　において、ｙ は上に凸である。
　　　　また、直線 ｙ＝（２/π）ｘ　は、（０，０）（π/２，１）を通るので、　ｓｉｎ ｘ ≧ （２/π）ｘ
　　　　　さらに、直線 ｙ＝ｘ　は、原点における ｙ＝ｓｉｎ ｘ　の接線で、ｙ’＝ｃｏｓ ｘ ≦１　より、
　　　　０≦ｘ≦π/２　において、　ｘ ≧ ｓｉｎ ｘ　が成り立つ。（証終）

　この証明に対して、次のような別証も当然考えられる。

（別証その１）　ｘ＝０　のときは、明らかに不等式は成り立つので、以下では、０＜ｘ≦π/２
　　　　　　　　として考える。
　　　　　　　　　Ｆ（ｘ）＝ｘ−ｓｉｎ ｘ　とおくと、　Ｆ’（ｘ）＝１−ｃｏｓ ｘ ＞０　より、
　　　　　　　　Ｆ（ｘ）は単調増加で、Ｆ（０）＝０　より、　Ｆ（ｘ）＞０　すなわち、　ｘ＞ｓｉｎ ｘ
　　　　　　　　　同様にして、　Ｇ（ｘ）＝ｓｉｎ ｘ − （２/π）ｘ　とおくと、
　　　　　　　　　Ｇ’（ｘ）＝ｃｏｓ ｘ − ２/π　となる。　Ｇ’（ｘ）＝０　となる ｘ の値を、α とすると、
　　　　　　　　Ｇ（ｘ）は、ｘ ＝α で、極大かつ最大である。
　　　　　　　　　Ｇ（０）＝Ｇ（π/２）＝０　より、　Ｇ（ｘ）≧０　すなわち、　ｓｉｎ ｘ ≧ （２/π）ｘ
　　　　　　　以上から、　０≦ｘ≦π/２　において、（２/π）ｘ ≦ ｓｉｎ ｘ ≦ ｘ　が成り立つ。（証終）

（別証その２）　ｘ＝０　のときは、明らかに不等式は成り立つので、以下では、０＜ｘ≦π/２
　　　　　　　　として考える。
　　　　　　　　　Ｆ（ｘ）＝ｘ−ｓｉｎ ｘ　とおくと、　Ｆ’（ｘ）＝１−ｃｏｓ ｘ ＞０　より、
　　　　　　　　Ｆ（ｘ）は単調増加で、Ｆ（０）＝０　より、　Ｆ（ｘ）＞０　すなわち、　ｘ＞ｓｉｎ ｘ
　　　　　　　　　同様にして、　Ｇ（ｘ）＝（ｓｉｎ ｘ ）/ｘ　とおくと、
　　　　　　　　　Ｇ’（ｘ）＝（ｘｃｏｓ ｘ − ｓｉｎ ｘ ）/ｘ²　となる。
　　　　　　　　そこで、　Ｈ（ｘ）＝ｘｃｏｓ ｘ − ｓｉｎ ｘ　とおくと、　Ｈ’（ｘ）＝−ｘ・ ｓｉｎ ｘ ＜０
　　　　　　　　　よって、Ｈ（ｘ）は単調減少で、Ｈ（０）＝０　より、　Ｈ（ｘ）＜０　なので、
　　　　　　　　Ｇ’（ｘ）＜０　すなわち、Ｇ（ｘ）は単調減少となる。
　　　　　　　　　Ｇ（π/２）＝２/π　なので、Ｇ（ｘ）≧２/π　すなわち、　ｓｉｎ ｘ ≧ （２/π）ｘ
　　　　　　　以上から、　０≦ｘ≦π/２　において、（２/π）ｘ ≦ ｓｉｎ ｘ ≦ ｘ　が成り立つ。（証終）

　以上３点証明を書いては見たが、やはり冒頭の図の説得力には到底太刀打ちできない。

　冒頭の図は有名なので誰でもどこかでは見ているものだろう。最近、視覚に訴える証明図
として、次のようなものもあることを知った。

　　　　　　　　

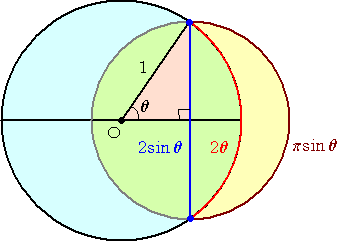
　証明は明らかであろう。