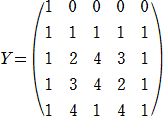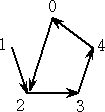有限図形の代数的表現 
当HPの読者のK.S.さんより、平成24年10月8日付けで標記話題をメールで頂いた。
三角形や星型の図形を式で表現したいという思いから、以下のことを考察しました。有限
個の点と辺で構成される図形を、整関数で表現する。そのため、基礎体として素数の有限
体を考える。但し、とりあえず扱うのは、点の数と辺の数が等しい特別な場合である。
先ず、P=5 のときから、始めることにします。
1.グラフと写像と関数について(特別な場合)
集合 F={0,1,2,3,4}について、写像 f : F → F を考える。このような写像は、55 個
あります。
f(0)=a、f(1)=b、f(2)=c、f(3)=d、f(4)=e
となる写像を、(a,b,c,d,e)m で表
す。
「次に、円周上に、5個の点を等間隔にとり、上(12時)から左回りに、0、1、2、3、4 と点
に名前をつけます。」
注意: この「」は、便宜上のことであり、これからの議論に、適用されない。
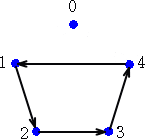
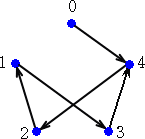
例えば、(1,2,3,4,1)m の表すグラフとは、有向グラフで
を表す。更に、ここで有限体F5上の関数を考えます。
f(x)=4x4+x3+4x2+2x+1 (ここで、 x≠0 → x4=1 )
f(0)=1、f(1)=2、f(2)=3、f(3)=4、f(4)=1
となるので、f(x)は上のグラフを表す
関数であることがわかります。
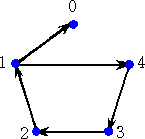
他に、五角形は、x+1 で、星形は、x+2 で表すことができます。
f(x)=A+Bx+Cx2+Dx3+Ex4 のとき、その係数をとって(A,B,C,D,E)p と表す。
F上の写像を、全て、F5(x)の4次以下の関数で表すことができる。写像と関数が
1対1に対応する。
(証明) f(x)=4x4+1 について、
f(0)=1、f(1)=0、f(2)=0、f(3)=0、f(4)=0
となるので、f(x)は、写像(1,0,0,0,0)m を表す。
よって、写像(a,b,c,d,e)m を表す関数は、
a(4x4+1)+b{4(x−1)4+1}+c{4(x−2)4+1}
+d{4(x−3)4+1}+e{4(x−4)4+1}
=(4a+4b+4c+4d+4e)x4+(4b+3c+2d+e)x3
+(4b+c+d+4e)x2+(4b+2c+3d+e)x+a
つまり、
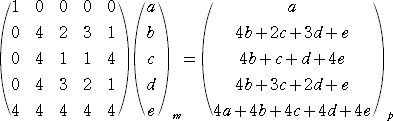
また逆に、4次以下の関数は、F上の写像を表す。
K.S.さんより続報です。(平成24年10月24日付け)
F上の写像から、F上の整関数への変換する行列をX、逆にF上の整関数からF上の写像
へ変換する行列をYとすると、おもしろい特徴があります。
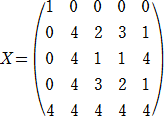 、
、 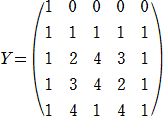
このとき、 XY=E 、X=2 、Y=3 が成り立つ。(X、Yをそれぞれ変換行列とよぶ)
「また、Xの各行は、関数 4x4+1、4x3、4x2、4x、4 の値になっている。
Yの各列は、関数 1、x、x2、x3、x4 の値になっている。」
一般のP(素数)の有限体上でも、X、Yについて同様のことが成り立つことが証明できます。
2.回転合同について
回転によって、重なるグラフを、回転合同(単に合同)と呼ぶことにする。つまり、似たよう
な形について、整式で特徴づけることができます。
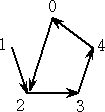
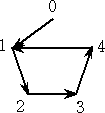
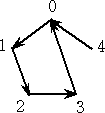
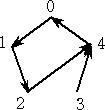
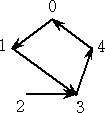
それぞれの関数は、
4x4+0x3+0x2+x+2 、 4x4+x3+4x2+2+1 、 4x4+2x3+x2+4x+1 、
4x4+3x3+x2+3x+1 、 4x4+4x3+4x2+0x+1
となり、最高次の係数が一致している。さらに、
4(x+α)4+(x+α)+2+4α (α=0、1、2、3、4)
と一つの式にまとめることができる。
一般に、
「回転合同であれば、標準形(次数−1次の項がない形)にまとめることができる。」
標準形
4次関数のとき、 A(x+α)4+B(x+α)2+C(x+α)+D+4α
3次関数のとき、 A(x+α)3+B(x+α)+C+4α
2次関数のとき、 A(x+α)2+B+4α
1次関数のとき、 A(x+α)+4α
「回転合同の5つの関数は、同じ次数であり、最高次の係数が同じであり、標準形によっ
て、一つにまとめることができる。そして、標準形で表した、5つの式は、回転合同である。」
K.S.さんより続報です。(平成24年11月15日付け)
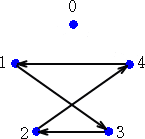
3.反転合同について
反転によって、重なるグラフを反転合同と呼ぶことにする。つまり
 |
→ |
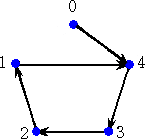 |
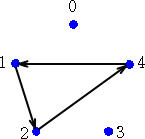
0軸対称のとき、1を4、2を3、3を2、4を1、0を0 すなわち、
(1,2,3,4,1)m → (4,4,1,2,3)m
式で表すと、 (1,2,4,1,4)p → (4,2,1,1,1)p
この変換を行列で表すと、対角成分が(4,1,4,1,4)で他の成分が0となる。反転した
式を求めるためには、この行列を掛ければよい。
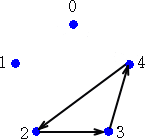
4.サイクル合同
二つの図形が、サイクルを持ち、その向きだけが、逆順になっているとき、サイクル合同
という。
三角形のサイクルは2種、四角形のサイクルは3種がある。
サイクルを持つ図形は、式を一つにまとめて表すことができる。パラメータαでまとめると、
a{4(x+α)4+1}+(x+α+3)3+4α+3
同様にして、サイクルが右回り=負の回転の場合は、
a{4(x+α)4+1}+(x+α+2)3+4α+2
a、αが等しければ、サイクル合同となる。他の場合、サイクルの右回りと左回りは、
a{4(x+α)4+1}+4(x+α+1)3+4α+1
a{4(x+α)4+1}+4(x+α+4)3+4α+4
a{4(x+α)4+1}+2(x+α+3)3+4α+4
a{4(x+α)4+1}+2(x+α+2)3+4α+1
a(x+α)(x+α+1)(x+α+4)(x+2α)+(x+α+1)2+4α
a(x+α)(x+α+1)(x+α+4)(x+2α)+4(x+α+4)2+4α
a(3x+α)(3x+α+1)(3x+α+4)(3x+2α)+2(3x+α+1)2+3α
a(3x+α)(3x+α+1)(3x+α+4)(3x+2α)+3(3x+α+4)2+3α
K.S.さんより続報です。(平成25年1月6日付け)
5.位相合同
写像の中で、特に、全単射のものを、置換と呼ぶ。全単射の関数(5!=120個)が対応
する。置換(番号の付け替え)によって位相的に、同型なグラフに移る。
σとτ-1στは位相的に同型である (σ、τは置換)
何故なら、互換(10通り)のとき位相同型が成り立つことがわかるので、一般のときも互
換の積で表されるので、成り立つことが分かる。
回転合同、反転合同、サイクル合同も、それぞれ対応する置換が存在するので、位相合
同(=位相同型)であることが分かる。
(具体例)

σ=(1,2,3,4,1)m σ’=(4,3,1,4,2)m
ここで、 τ=(14)(13)=(0,3,2,4,1)m とすると、
τ-1(1,2,3,4,1)mτ=(0,4,2,1,3)m・(1,2,3,4,1)m・(0,3,2,4,1)m
=(4,3,1,4,2)m
K.S.さんより続報です。(平成25年1月25日付け)
6.逆合同(矢印の向きが逆で、形が同じ)
これまでの写像は、一価の関数で表される。xとyを交換すると、逆関数を得る。一般に多
価の関数(陰関数)となる。
x+ay4+by3+cy2+dy+e=0 (55=3125個)
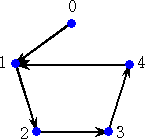
具体例 (1,2,3,4,1)m →(逆関数) (x,0,1,2,3)m または (x,4,1,2,3)m
 |
|
 |
y+x4+4x3+x2+3x+4=0 x+y4+4y3+y2+3y+4=0
逆写像どうしの積は、恒等写像ですが
(1,2,3,4,1)m(x,0,1,2,3)m=(x,1,2,3,4)m≡(0,1,2,3,4)m
(1,2,3,4,1)m(x,4,1,2,3)m=(x,1,2,3,4)m≡(0,1,2,3,4)m
また、
(x,0,1,2,3)m(1,2,3,4,1)m=(0,1,2,3,0)m≡(0,1,2,3,4)m
(x,4,1,2,3)m(1,2,3,4,1)m=(4,1,2,3,4)m≡(0,1,2,3,4)m
多重関数の場合、積の結果が多少異なるので、よりゆるい意味で同一視する必要がある。
グラフ的(写像的にも)には、
二重のループの点と、不定の点があるとき、ループを不定の点に移すことができる。そう
すれば、上の写像を同一視できる。
更に、多価の点があるとき、ループを持つどうしで互換があるとき、それを省くことができ
る。そうすれば、上の写像を同一視できる。
K.S.さんより続報です。(平成25年3月3日付け)
7.多価関数(多重グラフ)
逆関数を導入することによって、必然的に多価関数を導入することになった。これまで、一
価関数はグラフと一対一に対応がなされたが、多価関数では、複数の関数が、同じ一つの
グラフに対応することがある。一般には、関数は
a4(x)y4+a3(x)y3+a2(x)y2+a1(x)y+a0(x)=0 ai(x)はxの式
かなりの数の多重なグラフが生まれる。これを式の立場から、写像の立場から、グラフの立
場から同一視することを考えてみたい。
同じ値を持つが、式が異なる場合。
(イ) x3y2+1=0
(ロ) 3(x3+x)y2+1=0
(ハ) 2(x4+x2)y2+(3x4+2x3+3x2+2x+4)=0
(ニ) y2+x+3x4+2=0
(ホ) y2+x+2x4+3=0
零点以外は、等しいならば、同じ値をもち、グラフが同じになる。
F(x,y)=a4(x)y4+a3(x)y3+a2(x)y2+a1(x)y+a0(x)=0
G(x,y)=b4(x)y4+b3(x)y3+b2(x)y2+b1(x)y+b0(x)=0
y4+{a3(x)/a4(x)}y3+{a2(x)/a4(x)}y2+{a1(x)/a4(x)}y+{a0(x)/a4(x)}=0
y4+{b3(x)/b4(x)}y3+{b2(x)/b4(x)}y2+{b1(x)/b4(x)}y+{b0(x)/b4(x)}=0
a4(x)≠0 かつ b4(x)≠0 のとき、
ai(x)/a4(x)=ai(x)/a4(x) (i=0、1、2、3) ⇔ F(x,y)≡G(x,y)
代数的合同
と定義する。
同じ値を持つ場合は簡約してもよい具体例:
y=x2 → (0 1 4 4 1)m
x=y2 → (0 1 * * 2)m 、(0 4 * * 3)m
値0が重覆しているので、簡約する。
K.S.さんより続報です。(平成25年4月6日付け)
8.全単射の関数の次数
全単射を、グラフの立場から見ると、各点の次数がすべて2であること
写像の立場からみると、全射であること
関数の立場から見ると、
p=5のときは、1次関数のとき自明、3次関数のときは、標準形が
A(x+α)3+D+4α の形 A(4)×D(5)×b(5)=100通り
f(x):全単射 ⇒ af(x+y)+b:全単射 a≠0
p=7のときは、1次関数、4次関数、5次関数が全単射になる事がわかる。
ax+b a(6)×b(7)=42
a(x+y)4±3a(x+y)+c+4y a(6)×(±2)×y(7)×c(7)=588
a(x+y)5+c+4y a×c×y=6×7×7=294
a(x+y)5±3a(x+y)2+c+4y a×(±)×y×c=6×2×7×7=588
a(x+y)5+ba(x+y)3+3b2a(x+y)+4y a×b×c×y=6×6×7×7=1764
ax5+a(6b6+5b4+6b2)x3+a(3b5+2b3+3b)x2+3b2x
a×b×y×c=6×6×7×7=1764
7!=41+588+294+588+1764+1764
一般のときは、どういう次数が全単射になるか?


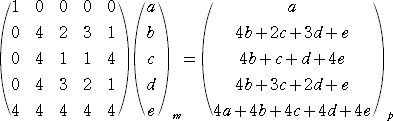
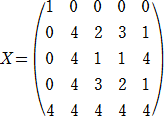 、
、