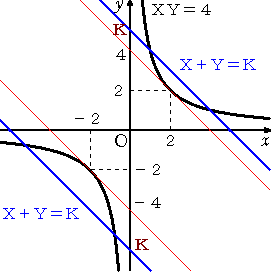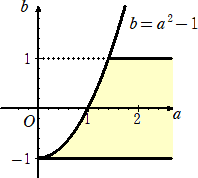グラフで考える 
生徒の行う計算を脇で見ていると、とても危なっかしいと思うことが度々ある。計算間違い
が多い生徒は、ほとんどといっていい位、計算の流れを把握しないまま頭でのみ行い、ノー
トには、数式の羅列があるばかりで、理路整然とした式変形の流れがそこにはない。
計算間違いを防ぐには、まず頭で計算することを止めさせ、式変形を逐一ノートに順番に
記入させ、今何を計算しているのか、なぜそのような式変形が必要なのかなどの理由を確
認させながら地道に計算に取り組ませるしかないだろう。
私自身のこれまでの経験から言えば、日本語も途中にしっかり入ったノートをとっている
生徒は計算ミスも少ないし、自分の言葉で数学を理解しているせいか、数学の応用力も十
分であるような気がする。
また、式の計算問題は、式の計算としか理解できない生徒も多くなっている。別な観点で
考えてみようという発想の柔軟性が最近の生徒から失われつつある。
代数的な問題を、幾何的な観点で考えようとする場合、「グラフ」というものが活躍する。
現在の学習指導要領では、直線、円(楕円も含む)、放物線、双曲線、3次曲線などを学
習するが、高校程度の代数的な問題を、幾何的な問題に翻訳するには十分である。
例 連立方程式 X+Y=K 、 XY=4 が(実数)解を持つように、定数
K の値の範囲
を定めよ。
(代数的な解答) X、Y は2次方程式 t2−Kt+4=0 の解
実数解を持つ条件は、判別式=K2−16≧0
よって、求めるKの値の範囲は、 K≦−4 、 4≦K
(コメント) この解答では、連立方程式の解法、実数条件、2次不等式の解法等、生徒にとっ
て苦手な計算が連続して出てくる。全国の高校生の通過率を予想すれば、かなり低いもの
となるであろう。
(幾何的な解答)
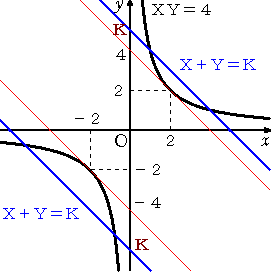 |
直線 X+Y=K と、 双曲線 XY=4
のグラフは左図の通りである。
連立方程式が(実数)解を持つためには、
両者が交わっていればよい。
よって、求めるKの値の範囲は、
K≦−4 、 4≦K
となる。 |
この例からも分かるように、代数的な解答では明確な計算方針を持っていないと迷路に
入ってしまう可能性があるが、幾何学的な解答では、「解をもつ」という条件が、よりヴィジ
ュアルな「交わる」という条件に置き換えられ、考え易くなっている。
代数的な問題を一度幾何的な問題に翻訳して解決策を探るということは、実は数学の世
界では常套手段である。よく「幾何で考え、代数でまとめる」という風に言われることである。
2次方程式に潜む不思議さを、この「グラフ」の力を借りて解明してみよう。そこには多分
多くの人がこれまでに経験したことがないだろう不思議な世界が待っているはずである。
いま、2次方程式 X2−6X+8=0 を考える。この2次方程式は因数分解されて、
(X−2)(X−4)=0 から、 解は、X= 2 , 4 となる。
よく知られているように、解と係数の関係から、2次方程式の X の係数と定数項は、2つ
の解の和と積によって表される。
6 = 2+4 (2つの解の和) , 8 = 2×4 (2つの解の積)
問 6 = 2+4 は代数的に正しい式であるが、幾何的にはどのような意味があるのだろ
うか?
2次方程式 X2−6X+8=0 を 放物線 Y=X2−6X+8 と X軸(Y=0)との関係で
考える。
 |
左図において、よく知られているように、放物線
は、軸 X=3 に関して線対称という性質を持つ。
数直線上で、点(3)は、点(2)と点(4)を結ぶ線
分の中点である。
よって、 3−2=4−3 より、
6 = 2+4
という式が解釈される。 |
実は、 6 = 2+4 という関係は、より一般な場合の性質を示唆している。
2次方程式 X2−6X+8=0 を上記とは違う組合せ、たとえば、
放物線 Y=X2 と 直線 Y=6X−8
との関係で考えてみよう。
 |
左図において、6 = 2+4 という関
係は、
AB+CD=6
という関係に翻訳される。
今度は直線を、Y=6X−4 としてみよ
う。
解の公式を用いて解を計算したり、また
は、解と係数の関係を知っていれば、
PQ+RS=6
が、やはり成り立つことに気づかされる。 |
このことから、放物線 Y=X2 と直線 Y=6X+k (k は定数) の交点について、
交点と Y 軸との距離の和は一定
(ただし、交点が第2象限のときは、距離の符号を負とする。)
という性質があることが分かる。
さらに突き詰めれば、2次方程式において、2つの解の和は、グラフで考えた場合、
直線のみに依存する量
であるということに気づかされる。
この性質に着目すれば、次のような驚くべき事実もごく自然に受け入れられることだろう。
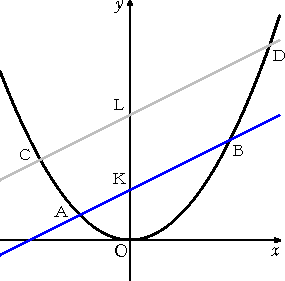 |
左図のような原点を頂点とする放物線
に、互いに平行な2直線が交わっている。
このとき、等式
KB−KA=LD−LC
が常に成り立つ。
(解の和の幾何学的意味に慣れていな
い人にとっては、大変な代数的計算を
しなければいけないことでしょう。) |
上記では、2次方程式の解の和に注目したが、今度は、解の積に着目してみよう。
問 8 = 2×4 は代数的に正しい式であるが、幾何的にはどのような意味があるのだろ
うか?
2次方程式 X2−6X+8=0 を 放物線 Y=X2+8 と 直線 Y=6X との関係で考
える。
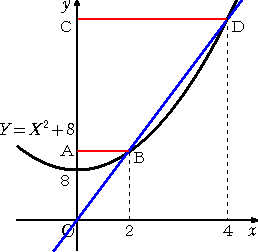 |
左図において、直線 Y=6X は原点を通り、
放物線の頂点と原点との距離が丁度 8 になっ
ている。
この値は、原点を通る直線の如何に関わらず
放物線だけに依存して定まる。
このとき、8 = 2×4 という式は
AB×CD = 8(=一定)
という関係式により、幾何的に解釈される。 |
このことから、放物線 Y=X2+8 と直線 Y=kX (k は定数) の交点について、
交点と Y 軸との距離の積は一定
(ただし、交点が第2象限のときは、距離の符号を負とする。)
という性質があることが分かる。
さらに突き詰めれば、2次方程式において、2つの解の積は、グラフで考えた場合、
放物線のみに依存する量
であるということに気づかされる。
一般に、任意の放物線と軸上の1点を通る任意の直線に対して、放物線と直線の2交点
と軸からの距離の積は常に一定であることが示される。
実際に、放物線 Y=aX2+b と 直線 Y=mX に対して、2交点を、(X1,Y1)、(X2,Y2)
とおく。(ただし、X1≠X2 と仮定する。)
このとき、
Y1=aX12+b 、 Y1=mX1 より、 mX1=aX12+b
Y2=aX22+b 、 Y2=mX2 より、 mX2=aX22+b
これらより、m を消去して、 X1・X2 = b/a (mによらず一定) を得る。
(コメント) この解と係数の関係は、教科書では、解の公式を用いて代数的な計算で求めら
れるのが普通である。このような放物線と直線の交点の関係で問題をとらえると、なぜ
か、スッキリした印象を受ける。)
この性質に着目すれば、次のような問題も簡単に解決されることだろう。
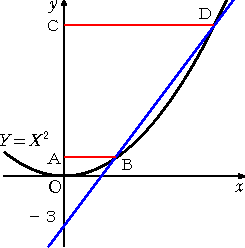 |
左図のような原点を頂点とする放物線に、Y軸
上の点(0,−3)を通る直線が2点で交わってい
る。
このとき、 AB×CD の値を求めよ。
解の積の幾何学的意味を理解していれば、即
座に答は、3 であると答えることができると思う。
|
(参考文献:D.ウェルズ 著 大橋義房 訳 みつけよう!数学! (岩波書店))
(追記) 令和7年10月23日付け
次の東北大学 前期文系(2001)の問題は、グラフの効用に感謝しなければならない。
問題 放物線 y=(x−p)2−2 が、3点(0,0)、(1,2)、(0,2) を頂点とする三角形と
交わるような実数pの範囲を求めよ。
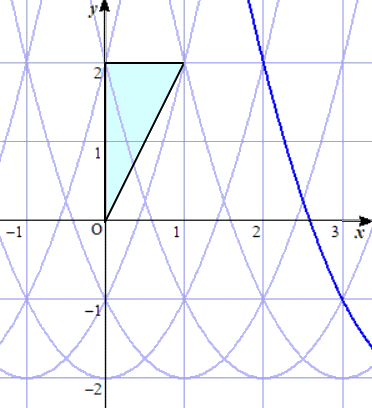
(解) 放物線 y=(x−p)2−2 が、点(0,2) を通るとき、p2−2=2、p<0 から、p=−2
放物線 y=(x−p)2−2 が、点(1,2) を通るとき、(1−p)2−2=2、p<0 から、p=−1
放物線 y=(x−p)2−2 が、点(0,0) を通るとき、p2−2=0、p>0 から、p=
放物線 y=(x−p)2−2 が、点(1,2) を通るとき、(1−p)2−2=2、p>0 から、p=3
以上から、グラフより、求める範囲は、 −2≦p≦−1 、 ≦p≦3 (終)
≦p≦3 (終)
(コメント) この問題は、計算だけではなかなか困難である。
(追記) 令和7年11月2日付け
次の東北大学 後期文系(2001)の問題も、グラフの効用に感謝する問題である。
問題 a、b を実数とし、F(x)=x2−2a|x|+b とする。|F(x)|=1 を満たす実数 x の個数
をNとする。
(1) a≦0 のとき、Nの最大値を求めよ。
(2) N=6 となるような点(a,b)の範囲をab平面上に図示せよ。
(解)(1) x≧0 のとき、 F(x)=x2−2ax+b=(x−a)2+b−a2
x<0 のとき、 F(x)=x2+2ax+b=(x+a)2+b−a2
a≦0 のとき、グラフは下図。
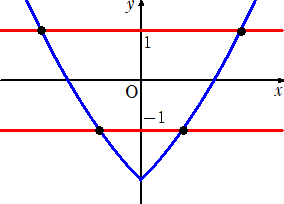
上図から、求めるNの最大値は、4
(2) (1)より、a>0 である。このとき、グラフは下図。
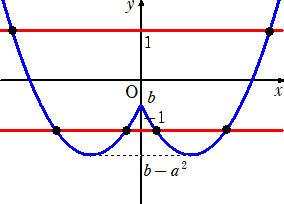
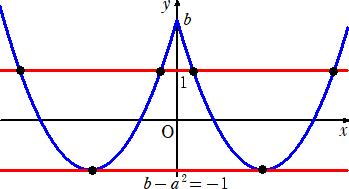
上図のとき、N=6 となるのは、 b−a2<−1<b で、かつ、 b<1 であればよいが、
特に、b−a2=−1 のときは、N=6 となるためには、 b>1 であればよい。
以上から、求める(a,b)の範囲は下図。
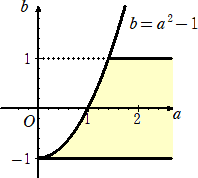
ただし、境界線は含まれないが、b=a2−1 (b>1) の部分のみ含む。 (終)
以下、工事中!