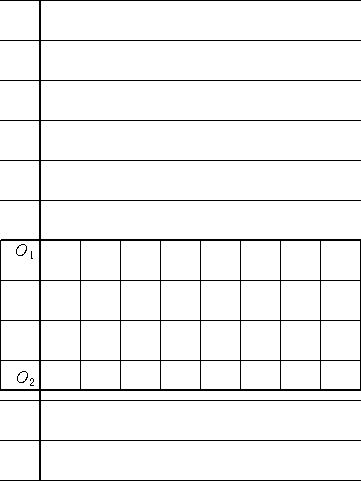
中学校では、２年生で、
のような、２元連立一次方程式を学ぶ。代入法とか加減法により、その解き方が指導され
る。
グラフを用いた次のような解法もよく知られている。
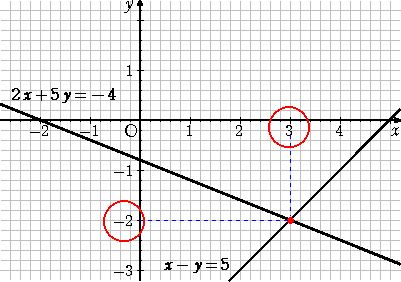
時間数削減の影響からか、もしかしたら、授業では扱われていないかもしれないが．．．。
このページで取り上げる解法は、実は、上記のものとは全く異質なものである。あまりに
複雑で、「実用性」に疑問符を打ちながら、「こんな解法もあるのか？」位のスタンスでご覧
いただけたら幸いである。
ただ、上記の鮮やかな解法は、残念ながら、未知数の個数が２の場合のみ有効である。
未知数の個数が３以上の場合は、途方に暮れてしまう。
ところが、これから紹介する方法は、複雑ではあるが、基本的に未知数の個数に制限は
ない。グラフを用いた一般の連立方程式の解法を与えているという意味で、大変素晴らし
いと思う。
実は最近、当ＨＰに掲載している「計算する図」に興味を持たれた方がいられて、いろい
ろとメールでお話を伺う機会がありました。このページは、その方を意識して作成しました。
先の連立方程式において、推論の明確化のために、文字を使って表すことにする。
すなわち、連立方程式
において、
である。
これらの
の値を数直線上に次のように目盛る。
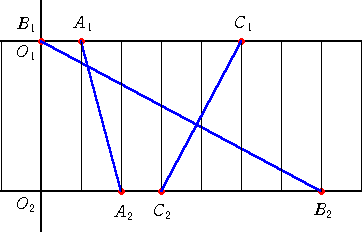
２つの数直線は互いに平行で、同じ目盛りで目盛られている。Ｏ1、Ｏ2 はそれぞれの原点
で、直線Ｏ1Ｏ2 は数直線と垂直に交わる。
数直線 Ｏ1 上に３点 Ａ1、Ｂ1、Ｃ1 を、Ｏ1Ａ1＝ａ1、Ａ1Ｂ1＝ｂ1（いま、ｂ1＜０ なので、Ｂ1は、
Ａ1 の左側に配置される！）、Ｂ1Ｃ1＝ｃ1 となるようにとる。
同様に、数直線 Ｏ2 上に３点 Ａ2、Ｂ2、Ｃ2 を、Ｏ2Ａ2＝ａ2、Ａ2Ｂ2＝ｂ2、Ｂ2Ｃ2＝ｃ2 （いま、
ｃ2＜０ なので、Ｃ2は、Ｂ2 の左側に配置される！）となるようにとる。
さらに、Ａ1 と Ａ2、Ｂ1 と Ｂ2、Ｃ1 と Ｃ2 を、それぞれ結んで、上記の図を得る。
いま、数直線と平行な直線 Ｌ を任意に引き、各線分との交点を、それぞれ Ａ 、Ｂ 、Ｃ とおく。
また、直線 Ｌ と直線Ｏ1Ｏ2 の交点を、Ｏ とおく。
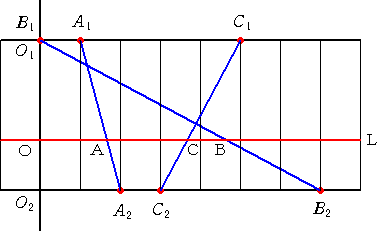
このとき、次の事実が知られている。
連立方程式
の解を、ｘ0 、ｙ0 とおくと、直線 Ｌ をどこに引いても、
が成り立つ。ただし、ＯＡ＝ａ 、ＡＢ＝ｂ 、ＢＣ＝ｃ （ 上図の場合、ｃ ＜０ ）である。
実際に、下図のように、点 Ｐ、Ｑ、Ｒ、Ｓ、Ｔ をとり、直線 Ｌ と数直線 Ｏ1 、数直線 Ｏ2 との
間の距離を、それぞれ ｍ 、ｎ とおく。
ただし、直線 Ｌ が数直線 Ｏ1 、数直線 Ｏ2 の間にあるときは、ｍ＞０、ｎ＞０
とし、直線 Ｌ が数直線 Ｏ1 の上方にあるときは、ｍ＜０、直線 Ｌ が数直線 Ｏ2 の
下方にあるときは、ｎ＜０ と考えることにする。
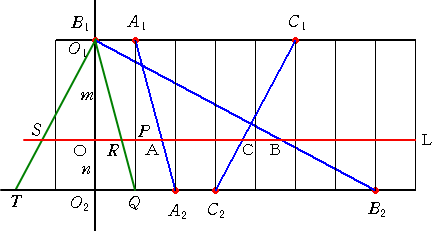
（上図で、Ｂ1Ｔ と Ｃ1Ｃ2 は平行である。）
このとき、ＱＡ2＝Ｏ2Ａ2−Ｏ2Ｑ＝Ｏ2Ａ2−Ｏ1Ａ1＝ａ2−ａ1
同様にして、
ＱＢ2＝ＱＡ2＋Ａ2Ｂ2＝Ｂ1Ａ1＋Ａ2Ｂ2＝Ａ2Ｂ2−Ａ1Ｂ1＝ｂ2−ｂ1
Ｂ2Ｔ＝Ｂ2Ｃ2＋Ｃ2Ｔ＝Ｂ2Ｃ2＋Ｃ1Ｂ1＝Ｂ2Ｃ2−Ｂ1Ｃ1＝ｃ2−ｃ1
が成り立つ。
また、△Ａ1ＰＡ∽△Ａ1ＱＡ2 、△Ｂ1ＲＢ∽△Ｂ1ＱＢ2 、△Ｂ1ＳＢ∽△Ｂ1ＴＢ2
で、相似比は、何れも、ｍ ： ｍ＋ｎ である。
したがって、簡単な計算により、
であることが分かる。
このことから、連立方程式の解を、ｘ0 、ｙ0 とおくと、
が成り立つことは明らかである。（証明終）
このとき、次のような場合が注目すべき点である。
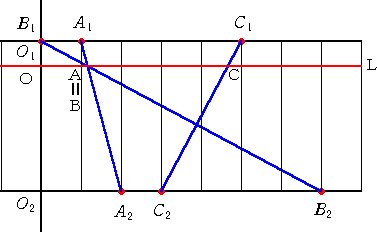
上図が示すことは、連立方程式の解 ｘ0 、ｙ0 に対して、
が成り立つということである。
を
に代入して、
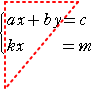
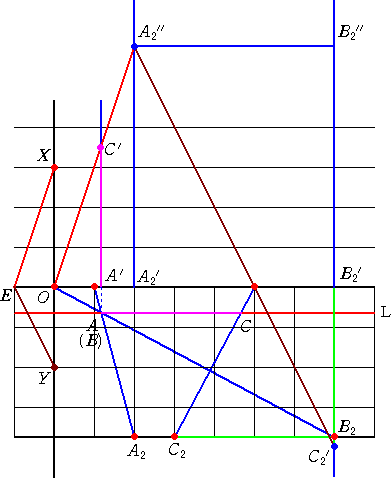（求め方）
