
生命は周りの環境の影響を受けて、その個体数の維持がなされているという。そのような
現象を予測する式として、ロジスティック写像なるものが知られている。
ある時刻 n における、ある個体の存在する密度を xn とおく。このとき、次の時刻 n+1
における、ある個体が存在する密度 xn+1 は、前の時刻の密度 xn から増える量はもちろ
ん、あとどれくらい増える可能性が残っているかということで、(1− xn )という量にも影響
を受けることは十分想像できる。
すなわち、閉じた空間に生息する生物は、ある程度までは増加するが、例えば、栄養難
などで、生命維持が困難になり、増加率が減少に転じることは十分理解できる。ある程度
個体数が減少したら、栄養補給の余剰から、また増加率が上昇するということも考えられ
る。
そこで、次のようなロジスティック写像が考えられる。(ロバート・メイ 1976年)
0≦a≦4 に対して、 xn+1=axn(1−xn) ただし、 0≦x0≦1
上記の「a」の値が微妙に、生命体の将来の状態に大きく関わってくる。この「a」の値を
繁殖率と理解すると分かりやすいだろう。
a=2 、 x0=0.001 として、その後の変化を図示してみると、
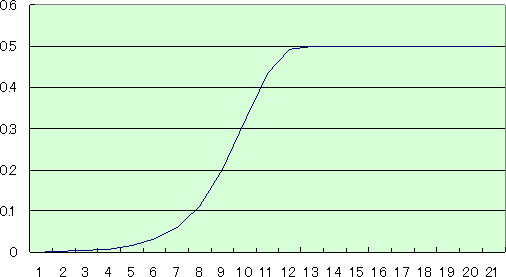
時間の経過とともに、一定値の「0.5」に近づいている様子が伺える。
ところが、 a=4 、 x0=0.001 として、その後の変化を図示してみると、
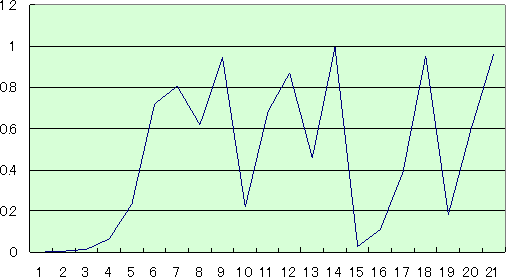
となって、まさに「混乱状態(カオス)」となっている。
漸化式 xn+1=4xn(1−xn) で定まる数列 { xn }は、簡単な2次関数
F(x)=4x(1−x)
を使って生成される。この2次関数が乱数発生の簡便な規則を与えることを最初に発見し
たのは、フォン・ノイマンとウラムと言われる。
数を生成する規則が定まっているのに、その規則から生成される数が不規則に変化す
るとは、とても不思議な現象だ。
また、 a=3.5 、 x0=0.001 として、その後の変化を図示してみると、
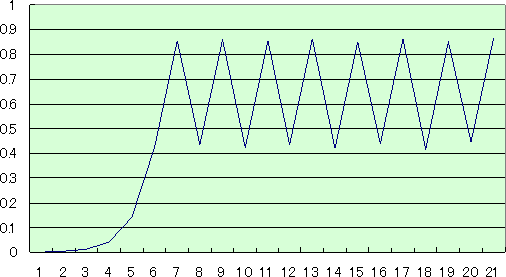
となって、いくつかの値の間を行ったり来たりするような振る舞いを示す。
また、 a=0.5 、 x0=0.001 として、その後の変化を図示してみると、
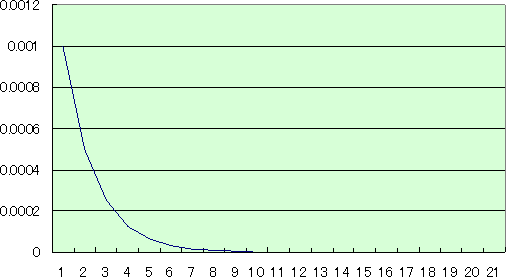
となって、時間の経過とともに、一定値の「0」に近づいている様子が伺える。
これでは、種の保存ができませんね!
簡単な写像の式で、a の値を適当に変えるだけで、これほどまでに異なる振る舞いを見
せてくれる、とても面白い写像と言える。
この写像に関して、次のことが知られているようだ。
0≦a≦1 のとき、 xn → 0
1<a≦2 のとき、 xn → 1−1/a (単調に!)
(→ 上記の計算で、a=2 のとき、確かに、xn → 0.5 )
2<a≦3 のとき、 xn → 1−1/a (振動しながら!)
3<a≦3.5699456・・・ のとき、 xn は、2 のべき乗個の間を振動するらしい!
3.5699456・・・<a≦4 のとき、 xn の値の変化は、不規則(カオス?)らしい!
(追記) 平成25年7月4日付け
最近、ある研究会に参加したとき、次のような問題が話題になった。
ある島で、100頭の羊がいる。その年、30頭の羊が生まれ、10頭が死んだ。羊の個体
数はこの後、どのように変化するだろうか?但し、その島の面積や植生などを考えて、その
島に生存できる羊は1000頭までと考えるものとする。
単純に考えれば、毎年1.2倍の増加率であるが、限界数があるので事はそう単純にはい
かないようだ。
これは、まさしく上記で話題になったロジスティック写像そのものである。あとどれくらい増
えることができるかという因子も関わってくるので、立式すれば、例えば、次のようなものに
なるだろう。
n年後の羊の個体数をanとおくと、
a1=100 、 (an+1−an)/an=(1000−an)/4500
ここで、「4500」という数字をいろいろいじってみると、様々な変化が見て取れる。生命は
そのどれを選択し、変化していくのだろう。興味はつきない。
以下、工事中