
丂偄偔偮偐偺梌偊傜傟偨忦審偐傜娭悢傪寛掕偡傞栤戣偼丄戝妛擖帋偺昿弌栤戣偩傠偆丅偙偺
儁乕僕偱偼丄偦偺傛偆側庬乆偺栤戣傪廤傔偰偄偙偆偲巚偆丅
丂師偼丄搶杒戝妛丂暥宯乮侾俋俈侾乯偺栤戣偱偁傞丅
栤戣丂丂娭悢 俥乮倶乯亖亅倶3亄倎倶2亄倐倶亄們 偑丄師偺俁偮偺忦審傪枮偨偡偲偒丄倎丄倐丄們 傪寛
丂丂掕偟偰丄娭悢 倷亖俥乮倶乯 偺僌儔僼偺奣宍傪昤偗丅
丂乮俙乯丂曽掱幃 俥乮倶乯亖侽 偺惓崻偼 倶亖侾 偩偗偱偁傞丅
丂乮俛乯丂俥乮倶乯 偼 倶亖侾 偱嬌抣傪偲傞丅
丂乮俠乯丂俀捈慄 倶亖侽丄倷亖侽 偍傛傃嬋慄 倷亖俥乮倶乯 偱埻傑傟偨晹暘偺柺愊偼俁/係偵摍偟偄丅
乮夝乯丂忦審乮俙乯乮俛乯傛傝丄丂俥乮倶乯亖亅乮倶亅兛乯乮倶亅侾乯2 乮兛亝侽乯丂偲偍偗傞丅
忦審乮俠乯傛傝丄丂亅佺01 俥乮倶乯倓倶亖俁/係丂偱偁傞丅
丂俥乮倶乯亖亅乮倶亅兛乯乮倶亅侾乯2亖亅乮倶亅侾乯3亄乮兛亅侾乯乮倶亅侾乯2丂偲幃曄宍偡傞偲丄
丂亅侾/係亅乮兛亅侾乯/俁亖俁/係丂傛傝丄丂兛亖亅俀
傛偭偰丄丂俥乮倶乯亖亅乮倶亄俀乯乮倶亅侾乯2亖亅倶3亄俁倶亅俀丂偲側傝丄丂倎亖侽丄倐亖俁丄們亖亅俀
俥乫乮倶乯亖亅俁倶2亄俁亖亅俁乮倶亄侾乯乮倶亅侾乯亖侽丂偲偍偔偲丄丂倶亖侾丄亅侾
憹尭昞傪挷傋傞偲丄
丂丂

傛偭偰丄僌儔僼偺奣宍偼壓恾偲側傞丅
丂丂
 丂丂乮廔乯
丂丂乮廔乯乮捛婰乯丂椷榓俇擭侾侾寧俀俋擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俈乯偺栤戣偼丄寁嶼偁傞偺傒偱偁傞丅
栤戣俀丂丂倎丄倐 傪惓偺惍悢偲偡傞丅娭悢 俥乮倶乯亖係倶3亅倎倶2亄俀倐倶亅俉 偑師偺俁偮偺忦審傪
丂丂摨帪偵枮偨偡傛偆側 倎丄倐 偺慻傪偡傋偰媮傔傛丅.
乮鶣乯丂俥乮侾乯亜侽
乮鶤乯丂俥乮倶乯偼嬌抣傪傕偮丅
乮鶥乯丂們値亖佺02n-1 俥乮倶乯倓倶丂乮値亖侾丄俀丄俁乯丂偱掕媊偝傟傞 們1丄們2丄們3 偑摍斾悢楍傪側偡丅
乮夝乯丂俥乮侾乯亖亅倎亄俀倐亅係亜侽丂傛傝丄丂倎亙俀倐亅係丂傑偨偼丄倐亜乮倎亄係乯/俀
丂俥乫乮倶乯亖侾俀倶2亅俀倎倶亄俀倐亖侽丂偲偍偔偲丄嬌抣傪帩偮偙偲偐傜丄丂倎2亅俀係倐亜侽
偡側傢偪丄丂倎2亜俀係倐丂傑偨偼丄丂倐亙倎2/俀係
們値亖[倶4亅乮倎/俁乯倶3亄倐倶2亅俉倶]02n-1丂傛傝丄
們1亖亅乮侾/俁乯倎亄倐亅俈
們2亖亅乮俉/俁乯倎亄係倐
們3亖亅乮俇係/俁乯倎亄侾俇倐亄俀俀係
忦審傛傝丄們1丄們2丄們3 偼摍斾悢楍傪側偡偺偱丄丂們22亖們1們3
傛偭偰丄丂乮亅乮俉/俁乯倎亄係倐乯2亖乮亅乮侾/俁乯倎亄倐亅俈乯乮亅乮俇係/俁乯倎亄侾俇倐亄俀俀係乯丂傛傝丄
丂倎倐亅侾係倎亅俀侾倐亄俀俋係亖侽丂偡側傢偪丄丂乮倎亅俀侾乯乮倐亅侾係乯亖侽
傛偭偰丄丂倎亖俀侾丂丄倐亖侾係
倎亖俀侾丂偺偲偒丄丂倐亜乮倎亄係乯/俀亖侾俀丏俆丂丄倐亙倎2/俀係亖侾係俈/俉亖侾俉丏俁俈俆
丂傛偭偰丄丂乮倎丆倐乯亖乮俀侾丆侾俁乯丄乮俀侾丆侾係乯丄乮俀侾丆侾俆乯丄乮俀侾丆侾俇乯丄乮俀侾丆侾俈乯丄乮俀侾丆侾俉乯
倐亖侾係丂偺偲偒丄丂倎亙俀倐亅係亖俀係丂丄倎2亜俀係倐亖俁俁俇丂傛傝丄丂倎亜併俁俁俇亖侾俉丏俁俁
丂傛偭偰丄丂乮倎丆倐乯亖乮侾俋丆侾係乯丄乮俀侽丆侾係乯丄乮俀侾丆侾係乯丄乮俀俀丆侾係乯丄乮俀俁丆侾係乯
埲忋偐傜丄媮傔傞 倎丄倐 偺慻乮倎丆倐乯偼丄埲壓偺侾侽屄偱偁傞丅
乮倎丆倐乯亖乮俀侾丆侾俁乯丄乮俀侾丆侾係乯丄乮俀侾丆侾俆乯丄乮俀侾丆侾俇乯丄乮俀侾丆侾俈乯丄乮俀侾丆侾俉乯丄
丂丂丂乮侾俋丆侾係乯丄乮俀侽丆侾係乯丄乮俀俀丆侾係乯丄乮俀俁丆侾係乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俁寧俀係擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋侽乯偺栤戣偼丄戣堄傪攃埇偡傞偺偵嬯楯偡傞偐傕偟傟側偄丅
栤戣丂丂俥乮倶乯亖倶2亅俀倶亄乮俈/侾俇乯佺-11 乥俥乮倶乯乥倓倶丂丒丒丒丂(*)丂傪枮偨偡娭悢俥乮倶乯偵偮偄
丂丂偰峫偊傞丅
乮侾乯丂倠傪晧偱側偄幚悢偲偡傞偲偒丄晄摍幃 佺-11 乥倶2亅俀倶亄倠乥倓倶亞係/俁亄倠丂偑惉傝棫
丂丂偮偙偲傪帵偣丅
乮俀乯丂俥乮倶乯亖倶2亅俀倶亄倠丂乮倠亞侾乯丂偺宍偺(*)偺夝傪媮傔傛丅
乮俁乯丂俥乮倶乯亖倶2亅俀倶亄倠丂乮侽亝倠亙侾乯丂偺宍偺(*)偺夝偼懚嵼偡傞偐丅懚嵼偡傞側傜偦偺夝
丂丂傪媮傔丄懚嵼偟側偄側傜偦偺偙偲傪帵偣丅
乮夝乯乮侾乯丂倶2亅俀倶亄倠亖乮倶亅侾乯2亄倠亅侾丂傛傝丄丂幉偺幃偼丄丂倶亖侾
丂倠亞侾丂偺偲偒丄丂倠亅侾亞侽丂偱丄丂倶2亅俀倶亄倠亞侽
偙偺偲偒丄丂佺-11 乥倶2亅俀倶亄倠乥倓倶亖佺-11 乮倶2亅俀倶亄倠乯倓倶亖俀/俁亄俀倠
丂俀/俁亄俀倠亅乮係/俁亄倠乯亖倠亅俀/俁亜侽丂側偺偱丄丂俀/俁亄俀倠亜係/俁亄倠
傛偭偰丄丂倠亞侾丂偺偲偒丄丂佺-11 乥倶2亅俀倶亄倠乥倓倶亞係/俁亄倠丂偼惉傝棫偮丅
侽亝倠亙侾丂偲偡傞丅丂倶2亅俀倶亄倠亖侽丂傪夝偔偲丄丂倶亖侾亇併乮侾亅倠乯
偙偺偲偒丄丂亅侾亙侾亅併乮侾亅倠乯亙侾丂偱偁傞丅
傛偭偰丄
佺-11 乥倶2亅俀倶亄倠乥倓倶
亖佺-11-併(1-k乯 乮乮倶亅侾乯2亄倠亅侾乯倓倶亄佺1-併(1-k乯1 乮亅乮倶亅侾乯2亅倠亄侾乯倓倶
亖[乮倶亅侾乯3/俁亅乮侾亅倠乯倶]-11-併(1-k乯亄[亅乮倶亅侾乯3/俁亄乮侾亅倠乯倶]1-併(1-k乯1
亖亅乮併乮侾亅倠乯乯3/俁亅乮侾亅倠乯乮侾亅併乮侾亅倠乯乯亄俉/俁亅乮侾亅倠乯
丂亄乮侾亅倠乯亅乮併乮侾亅倠乯乯3/俁亅乮侾亅倠乯乮侾亅併乮侾亅倠乯乯
亖亅俀乮併乮侾亅倠乯乯3/俁亅俀乮侾亅倠乯乮侾亅併乮侾亅倠乯乯亄俉/俁
亖係乮併乮侾亅倠乯乯3/俁亄俀倠亄俀/俁
侽亝倠亙侾丂偺偲偒丄丂併乮侾亅倠乯亞侾亅倠丂側偺偱丄
丂係乮併乮侾亅倠乯乯3/俁亄俀倠亄俀/俁亞係乮侾亅倠乯3/俁亄俀倠亄俀/俁
偙偙偱丄丂倷亖係乮侾亅倠乯3/俁亄俀倠亄俀/俁亅乮係/俁亄倠乯丂偲偍偔偲丄丂倷乫亖係乮侾亅倠乯2亄侾亜侽
偐傜丄倷偼扨挷偵憹壛偡傞丅丂倠亖侽丂偺偲偒丄丂倷亖係/俁亄俀/俁亅係/俁亖俀/俁亜侽丂側偺偱丄
丂侽亝倠亙侾丂偺偲偒丄丂佺-11 乥倶2亅俀倶亄倠乥倓倶亞係/俁亄倠丂偼惉傝棫偮丅
埲忋偐傜丄晧偱側偄幚悢倠偵懳偟偰丄佺-11 乥倶2亅俀倶亄倠乥倓倶亞係/俁亄倠丂偑惉傝棫偮丅
乮俀乯丂倠亞侾丂偺偲偒丄丂乮俈/侾俇乯乮俀/俁亄俀倠乯亖倠丂傪夝偄偰丄丂倠亖俈/俁
丂傛偭偰丄丂俥乮倶乯亖倶2亅俀倶亄俈/俁
乮俁乯丂侽亝倠亙侾丂偺偲偒丄丂乮俈/侾俇乯乮係乮併乮侾亅倠乯乯3/俁亄俀倠亄俀/俁乯亖倠丂傛傝丄
丂係乮併乮侾亅倠乯乯3/俁亖乮俀/俈乯倠亅俀/俁
丂嵍曈偼惓偱丄塃曈偼晧側偺偱丄忋幃傪枮偨偡幚悢倠偼懚嵼偟側偄丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俁寧俁侾擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋侾乯偺栤戣偼丄寁嶼偵嬯楯偡傞偐傕偟傟側偄丅
栤戣
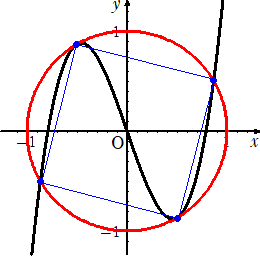
乮侾乯丂墌 倶2亄倷2亖侾 偵撪愙偡傞惓曽宍偺侾偮偺捀揰偺嵗昗傪(倫丆倯)偲偡傞偲偒丄巆傝偺捀揰
丂丂偺嵗昗傪倫偲倯偱昞偣丅
乮俀乯丂俥乮倶乯亖倎倶3亄倐倶2亄們倶亄倓 乮倎亗侽乯 偲偡傞丅嬋慄 倷亖俥乮倶乯 偼墌 倶2亄倷2亖侾 偲係揰偺
丂丂傒傪嫟桳偟丄偙傟傜偺係揰偼丄偁傞惓曽宍偺捀揰偵側偭偰偄傞丅俥乮倶乯傪媮傔傛丅
乮夝乯乮侾乯丂暋慺悢暯柺偱峫偊傞偲丄倝 傪嫊悢扨埵偲偟偰丄
丂乮倫亄倯倝乯丒倝亖亅倯亄倫倝丂丄乮亅倯亄倫倝乯丒倝亖亅倫亅倯倝丂丄乮亅倫亅倯倝乯丒倝亖倯亅倫倝
傛傝丄(倫丆倯)埲奜偺捀揰偺嵗昗偼丄丂乮亅倯丆倫乯丂丄乮亅倫丆亅倯乯丂丄乮倯丆亅倫乯丂偱偁傞丅
乮俀乯丂俥乮倶乯亖倎倶3亄倐倶2亄們倶亄倓丂偼丄(倫丆倯)丂丄乮亅倫丆亅倯乯傪捠傞偺偱丄
丂倎倫3亄倐倫2亄們倫亄倓亖倯丂丄亅倎倫3亄倐倫2亅們倫亄倓亖亅倯
偙傟傛傝丄丂倐倫2亄倓亖侽丂丄倎倫3亄們倫亖倯
丂摨條偵丄乮亅倯丆倫乯丂丄乮倯丆亅倫乯丂傪捠傞偺偱丄
丂亅倎倯3亄倐倯2亅們倯亄倓亖倫丂丄倎倯3亄倐倯2亄們倯亄倓亖亅倫
偙傟傛傝丄丂倐倯2亄倓亖侽丂丄亅倎倯3亅們倯亖倫
傛偭偰丄丂倐乮倫2亅倯2乯亖侽丂偲側傞丅
倫2亅倯2亖侽丂偡側傢偪丄丂倯亖亇倫丂偺偲偒丄惓曽宍偺懳曈偑 倷 幉偵暯峴偵側傝丄係捀揰傪捠
傞俁師娭悢偺僌儔僼偼懚嵼偟側偄丅
丂傛偭偰丄倫2亅倯2亗侽丂偱丄偙偺偲偒丄丂倐亖侽丄倓亖侽丂偲側傞丅
偟偨偑偭偰丄丂俥乮倶乯亖倎倶3亄們倶丂乮倎亗侽乯
楢棫偟偰丄丂倶2亄乮倎倶3亄們倶乯2亖侾丂偡側傢偪丄丂倎2倶6亄俀倎們倶4亄乮們2亄侾乯倶2亖侾
倶2亖倃丂偲偍偔偲丄丂倎2倃3亄俀倎們倃2亄乮們2亄侾乯倃亅侾亖侽
丂俧乮倶乯亖倎2倃3亄俀倎們倃2亄乮們2亄侾乯倃亅侾丂偲偍偔丅
丂俧乮侽乯亖亅侾亙侽丂丄俧乮侾乯亖倎2亄俀倎們亄們2亖乮倎亄們乯2亞侽丂側偺偱丄
丂戣堄傪枮偨偡俁師娭悢偑懚嵼偡傞偨傔偵偼丄俧乮倶乯亖侽丂偑丄侽偲侾偺娫偵丄俀偮偺惓偺夝
兛丄兝乮偨偩偟丄兛亙兝 偱丄兛偼廳夝乯傪帩偰偽傛偄丅
丂丂
丂傑偨丄乮併兛丆亅併兝乯丄(併兝丆併兛) 偼丄墌 倶2亄倷2亖侾 忋偺揰側偺偱丄丂兛亄兝亖侾
偝傜偵丄丂倎2倃3亄俀倎們倃2亄乮們2亄侾乯倃亅侾亖倎2乮倃亅兛乯2乮倃亅兝乯丂偺學悢傪斾妑偟偰丄
丂俀兛亄兝亖亅俀們/倎丂丄兛2亄俀兛兝亖乮們2亄侾乯/倎2丂丄兛2兝亖侾/倎2
偙偙偱丄丂們/倎亖倠丂偲偍偔偲丄俀兛亄兝亖亅俀倠丂丄兛2亄俀兛兝亖倠2亄兛2兝
兝亖侾亅兛丂傪戙擖偟偰丄丂侾亄兛亖亅俀倠丂偡側傢偪丄丂倠亖亅乮侾亄兛乯/俀
丂兛2亄俀兛兝亅兛2兝亖倠2丂傛傝丄丂兛3亄俀兛乮侾亅兛乯亖倠2丂偡側傢偪丄
丂兛3亅俀兛2亄俀兛亖倠2
倠亖亅乮侾亄兛乯/俀丂傪戙擖偟偰丄丂兛3亅俀兛2亄俀兛亖乮侾亄兛乯2/係
丂偡側傢偪丄丂係兛3亅俋兛2亄俇兛亅侾亖侽丂傛傝丄丂乮兛亅侾乯2乮係兛亅侾乯亖侽
丂兛亗侾丂側偺偱丄丂兛亖侾/係丂偙偺偲偒丄丂兝亖俁/係丂傛傝丄
丂倎2亖俇係/俁丂偐傜丄丂倎亖俉/
傑偨丄倠亖亅俆/俉丂傛傝丄丂們亖倎倠亖乮俉/
丂埲忋偐傜丄丂俥乮倶乯亖乮俉倶3亅俆倶乯/
丂偙偺娭悢傪 倶 幉偵娭偟偰懳徧堏摦偝偣偰傕忦審傪枮偨偡偺偱丄
丂俥乮倶乯亖亅乮俉倶3亅俆倶乯/
埲忋偐傜丄媮傔傞娭悢偼丄丂俥乮倶乯亖亇乮俉倶3亅俆倶乯/
乮僐儊儞僩乯丂偐側傝僴乕僪側寁嶼偱偟偨両帋尡帪娫撪偵夝偒偒傞偙偲偼擄偟偄偐傕丏丏丏丅
乮捛婰乯丂椷榓俈擭俆寧侾俆擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俁乯偺栤戣偼丄掕斣偺娭悢寛掕栤戣偱偁傞丅
栤戣丂丂師偺俀偮偺摍幃傪摨帪偵枮偨偡娭悢俥乮倶乯偲俧乮倶乯傪峫偊傞丅
丂丂俥乮倶乯亖倶2亄佺-11 乮倶亅倲乯俧乮倲乯倓倲丂丄俧乮倶乯亖佺-11 乮乮俁/俀乯俥乮倲亅倶乯亄倶俧乮倲乯乯倓倲
乮侾乯丂俥乮倶乯偼 倶 偺俀師幃偱偁傞偙偲傪帵偣丅
乮俀乯丂俥乮倶乯偲俧乮倶乯傪媮傔傛丅
乮夝乯乮侾乯丂俥乮倶乯亖倶2亄倶佺-11 俧乮倲乯倓倲亅佺-11 倲俧乮倲乯倓倲丂偱丄
丂佺-11 俧乮倲乯倓倲亖倎丄佺-11 倲俧乮倲乯倓倲亖倐丂偲偍偔偲丄倎丄倐偼掕悢偱丄
丂俥乮倶乯亖倶2亄倎倶亅倐丂偼丄倶 偺俀師幃偲側傞丅
乮俀乯丂俧乮倶乯亖乮俁/俀乯佺-11 俥乮倲亅倶乯倓倲亄倶佺-11 俧乮倲乯倓倲亖乮俁/俀乯佺-11 俥乮倲亅倶乯倓倲亄倎倶
偙偙偱丄倲亅倶亖兤丂偲偍偔偲丄倓倲亖倓兤丂偱丄
丂佺-11 俥乮倲亅倶乯倓倲亖佺-1-x1-x 俥乮兤乯倓兤亖佺-1-x1-x 乮兤2亄倎兤亅倐乯倓兤
亖[兤3/俁亄倎兤2/俀亅倐兤]-1-x1-x
亖乮乮侾亅倶乯3亅乮亅侾亅倶乯3乯/俁亄倎乮乮侾亅倶乯2亅乮亅侾亅倶乯2乯/俀亅倐乮乮侾亅倶乯亅乮亅侾亅倶乯乯
亖乮俀亄俇倶2乯/俁亅俀倎倶亅俀倐
傛傝丄丂俧乮倶乯亖侾亄俁倶2亅俁倎倶亅俁倐亄倎倶亖俁倶2亅俀倎倶亅俁倐亄侾丂偲側傞丅
傛偭偰丄丂倎亖佺-11 乮俁倲2亅俀倎倲亅俁倐亄侾乯倓倲亖俀佺01 乮俁倲2亅俁倐亄侾乯倓倲 傛傝丄
丂倎亖俀乮侾亅俁倐亄侾乯亖係亅俇倐
傑偨丄丂倐亖佺-11 乮俁倲3亅俀倎倲2亅乮俁倐亅侾乯倲乯倓倲亖亅係倎佺01 倲2倓倲亖亅乮係/俁乯倎
傛偭偰丄丂倎亖係亄俉倎丂傛傝丄丂倎亖亅係/俈丂丄倐亖侾俇/俀侾
埲忋偐傜丄丂俥乮倶乯亖倶2亅乮係/俈乯倶亅侾俇/俀侾
丂俧乮倶乯亖俁倶2亄乮俉/俈乯倶亅俋/俈丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧俇擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋係乯偺栤戣偼丄側偐側偐柺敀偄丅
栤戣丂丂旝暘壜擻側娭悢俥乮倶乯偑丄偁傞掕悢倎亗侽偵懳偟偰丄俥乫乮倶乯亖倎俥乮侾亅倶乯傪枮偨偟丄
丂丂倶亖侽偱嵟戝抣俀傪偲傞偲偡傞丅俧乮倶乯亖乷俥乮倶乯乸2亄乷俥乮侾亅倶乯乸2 偲偍偔丅
乮侾乯丂俧乮倶乯偼 倶 偵傛傜側偄掕悢偱偁傞偙偲傪帵偣丅
乮俀乯丂俧乮倶乯傪媮傔傛丅
乮俁乯丂愊暘佺01 乷俥乮倶乯乸2倓倶 偺抣傪媮傔傛丅
乮夝乯乮侾乯丂俧乫乮倶乯亖俀俥乮倶乯俥乫乮倶乯亄俀俥乮侾亅倶乯俥乫乮侾亅倶乯乮亅侾乯
丂忦審傛傝丄丂俥乫乮倶乯亖倎俥乮侾亅倶乯丂丄俥乫乮侾亅倶乯亖倎俥乮倶乯丂側偺偱丄
丂俧乫乮倶乯亖俀俥乮倶乯丒倎俥乮侾亅倶乯亅俀俥乮侾亅倶乯丒倎俥乮倶乯亖侽
丂傛偭偰丄俧乮倶乯偼 倶 偵傛傜側偄掕悢偱偁傞丅
乮俀乯丂戣堄傛傝丄俥乮侽乯亖俀丄俥乫乮侽乯亖侽丂側偺偱丄倎俥乮侾乯亖俥乫乮侽乯亖侽丂偐傜丄俥乮侾乯亖侽
傛偭偰丄丂俧乮侾乯亖乷俥乮侾乯乸2亄乷俥乮侽乯乸2亖係丂偐傜丄丂俧乮倶乯亖係
乮俁乯丂係亖佺01 乷俥乮倶乯乸2倓倶亄佺01 乷俥乮侾亅倶乯乸2倓倶
丂偙偙偱丄侾亅倶亖倲丂偲偍偔偲丄丂倓倶亖亅倓倲丂側偺偱丄
丂佺01 乷俥乮侾亅倶乯乸2倓倶亖亅佺10 乷俥乮倲乯乸2倓倲亖佺01 乷俥乮倶乯乸2倓倶
傛偭偰丄丂佺01 乷俥乮倶乯乸2倓倶亖係亐俀亖俀丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧侾俋擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俆乯偺栤戣偼丄偨偩寁嶼偡傞偺傒偱偁傞丅
栤戣丂丂値亖侽丄侾丄俀丄俁 偵懳偟丄佺-11 倶n俥乮倶乯倓倶亖侽 傪摨帪偵枮偨偡係師幃俥乮倶乯傪媮傔
丂丂傛丅偨偩偟丄俥乮倶乯偺 倶4 偺學悢偼侾偲偡傞丅
乮夝乯丂俥乮倶乯亖倶4亄倎倶3亄倐倶2亄們倶亄倓丂偲偍偔丅
佺-11 俥乮倶乯倓倶亖侽 偐傜丄俀佺01 乮倶4亄倐倶2亄倓乯倓倶亖侽 傛傝丄丂俀/俆亄俀倐/俁亄俀倓亖侽
偡側傢偪丄丂侾/俆亄倐/俁亄倓亖侽
佺-11 倶俥乮倶乯倓倶亖侽 偐傜丄俀佺01 乮倎倶4亄們倶2乯倓倶亖侽 傛傝丄丂俀倎/俆亄俀們/俁亖侽
偡側傢偪丄丂倎/俆亄們/俁亖侽
佺-11 倶2俥乮倶乯倓倶亖侽 偐傜丄俀佺01 乮倶6亄倐倶4亄倓倶2乯倓倶亖侽 傛傝丄丂俀/俈亄俀倐/俆亄俀倓/俁亖侽
偡側傢偪丄丂侾/俈亄倐/俆亄倓/俁亖侽
佺-11 倶3俥乮倶乯倓倶亖侽 偐傜丄俀佺01 乮倎倶6亄們倶4乯倓倶亖侽 傛傝丄丂俀倎/俈亄俀們/俆亖侽
偡側傢偪丄丂倎/俈亄們/俆亖侽
偙偺偲偒丄丂倎/俆亄們/俁亖侽丂丄倎/俈亄們/俆亖侽丂偐傜丄丂倎亖們亖侽
丂侾/俆亄倐/俁亄倓亖侽丂丄侾/俈亄倐/俆亄倓/俁亖侽丂偐傜丄丂倐亖亅俇/俈丂丄倓亖俁/俁俆
傛偭偰丄丂俥乮倶乯亖倶4亅乮俇/俈乯倶2亄俁/俁俆丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧侾擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮侾俋俋俇乯偺栤戣傕丄扨側傞寁嶼栤戣偱偁傞丅
栤戣丂丂 俁師娭悢 俥乮倶乯亖倶3亅倫倶 偼丄倶亖倎 偵偍偄偰嬌戝抣倐傪偲傞偲偡傞丅揰俹乮倎丆倐乯傪尨
丂丂揰傪拞怱偵惓偺岦偒偵俋侽亱夞揮偟偨揰傪俻偲偡傞丅嬋慄 倷亖俥乮倶乯偑揰俻傪捠傞傛偆側倫偺
丂丂抣傪媮傔傛丅
乮夝乯丂俥乫乮倶乯亖俁倶2亅倫亖侽丂偱丄嬌戝抣偑懚嵼偡傞偙偲偐傜丄丂倫亜侽丂偱偁傞丅
丂偙偺偲偒丄丂倶亖亅併乮倫/俁乯丂偱嬌戝偱丄嬌戝抣偼丄丂俀乮倫/俁乯併乮倫/俁乯
丂傛偭偰丄丂倎亖亅併乮倫/俁乯丂丄倐亖俀乮倫/俁乯併乮倫/俁乯
丂偙偺偲偒丄丂俻乮亅俀乮倫/俁乯併乮倫/俁乯丆亅併乮倫/俁乯乯丂偱偁傞丅
傛偭偰丄丂亅俉乮倫/俁乯3丒乮倫/俁乯併乮倫/俁乯亄俀倫丒乮倫/俁乯併乮倫/俁乯亖亅併乮倫/俁乯
偡側傢偪丄丂亅俉倫4/俉侾亄俀倫2/俁亖亅侾丂傛傝丄丂倫4亅乮俀俈/係乯倫2亅俉侾/俉亖侽
偙偺偲偒丄丂倫2亖乮俀俈亄俋
丂倫亖俁併乮俁亄
乮捛婰乯丂椷榓俈擭俈寧侾係擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俇乯偺栤戣傕丄傛偔偁傞掕斣栤戣偱偁傞丅
栤戣丂丂俥乮倶乯傪楢懕側娭悢偲偡傞丅偡傋偰偺 倶 偵懳偟偰丄
丂丂俥乮倶乯亖倱倝値倶亄乮侾/兾乯佺0兾 俥乮倲乯們倧倱乮倶亅倲乯倓倲
偑惉傝棫偮偲偒丄俥乮倶乯傪媮傔傛丅
乮夝乯丂俥乮倶乯亖倱倝値倶亄乮侾/兾乯佺0兾 俥乮倲乯乮們倧倱倶們倧倱倲亄倱倝値倶倱倝値倲乯倓倲
丂丂亖倱倝値倶亄乮侾/兾乯乮們倧倱倶佺0兾 俥乮倲乯們倧倱倲倓倲亄倱倝値倶佺0兾 俥乮倲乯倱倝値倲倓倲乯
偙偙偱丄丂佺0兾 俥乮倲乯們倧倱倲倓倲亖俙丄佺0兾 俥乮倲乯倱倝値倲倓倲亖俛丂偲偍偔偲丄
丂俥乮倶乯亖倱倝値倶亄乮侾/兾乯乮俙們倧倱倶亄俛倱倝値倶乯
偙偺偲偒丄
俙亖佺0兾 乮倱倝値倲亄乮侾/兾乯乮俙們倧倱倲亄俛倱倝値倲乯乯們倧倱倲倓倲
丂亖佺0兾 乮乮侾/俀乯倱倝値俀倲亄乮侾/兾乯乮乮俙/俀乯乮侾亄們倧倱俀倲乯亄乮俛/俀乯倱倝値俀倲乯倓倲
丂亖亅乮侾/係乯[們倧倱俀倲]0兾亄乮俙/乮俀兾乯乯[倲亄乮侾/俀乯倱倝値俀倲]0兾亅乮俛/乮係兾乯乯[們倧倱俀倲]0兾
丂亖俙/俀丂傛傝丄丂俙亖侽
俛亖佺0兾 乮侾亄乮俛/兾乯乯倱倝値2倲倓倲
丂亖乷乮侾亄乮俛/兾乯乯/俀乸佺0兾 乮侾亅們倧倱俀倲乯倓倲
丂亖乷乮侾亄乮俛/兾乯乯/俀乸[倲亅乮侾/俀乯倱倝値俀倲]0兾
丂亖兾/俀亄俛/俀丂傛傝丄丂俛亖兾
偟偨偑偭偰丄丂俥乮倶乯亖倱倝値倶亄乮侾/兾乯兾倱倝値倶亖俀倱倝値倶丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧俁侾擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俈乯偺栤戣傕丄傛偔偁傞掕斣栤戣偱偁傞丅
栤戣丂丂師偺摍幃傪枮偨偡楢懕側娭悢俥乮倶乯偵偮偄偰峫偊傞丅
丂丂佺0x 乮俥乮倲乯亅倲亄侾乯倓倲亖佺-11 乮倶亅倲乯3俥乮倲乯倓倲亄俀/俀俆
乮侾乯丂俥乮倶乯偼 倶 偺俀師幃偱偁傞偙偲傪帵偣丅
乮俀乯丂俥乮倶乯傪媮傔傛丅
乮夝乯乮侾乯丂佺-11 乮倶亅倲乯3俥乮倲乯倓倲
丂亖倶3佺-11 俥乮倲乯倓倲亅俁倶2佺-11 倲俥乮倲乯倓倲亄俁倶佺-11 倲2俥乮倲乯倓倲亅佺-11 倲3俥乮倲乯倓倲
偵偍偄偰丄
丂俙亖佺-11 俥乮倲乯倓倲丂丄俛亖佺-11 倲俥乮倲乯倓倲丂丄俠亖佺-11 倲2俥乮倲乯倓倲丂丄俢亖佺-11 倲3俥乮倲乯倓倲
偲偍偔偲丄丂佺0x 乮俥乮倲乯亅倲亄侾乯倓倲亖俙倶3亅俁俛倶2亄俁俠倶亅俢亄俀/俀俆
椉曈傪旝暘偟偰丄丂俥乮倶乯亅倶亄侾亖俁俙倶2亅俇俛倶亄俁俠丂傛傝丄
丂俥乮倶乯亖俁俙倶2亄乮侾亅俇俛乯倶亄俁俠亅侾
傛偭偰丄俥乮倶乯偼 倶 偺俀師幃偱偁傞丅
乮俀乯丂俙亖佺-11 俥乮倲乯倓倲亖俀佺01 乮俁俙倲2亄俁俠亅侾乯倓倲亖俀乮俙亄俁俠亅侾乯
丂偡側傢偪丄丂俙亄俇俠亅俀亖侽
丂俛亖佺-11 倲俥乮倲乯倓倲亖俀乮侾亅俇俛乯佺01 倲2倓倲亖俀乮侾亅俇俛乯/俁丂偡側傢偪丄丂侾俆俛亖俀
丂傛偭偰丄丂俛亖俀/侾俆
丂俠亖佺-11 倲2俥乮倲乯倓倲亖俀佺01 乮俁俙倲4亄乮俁俠亅侾乯倲2乯倓倲亖俇俙/俆亄乮俇俠亅俀乯/俁
丂偡側傢偪丄丂侾俉俙亄侾俆俠亖侾侽
丂偙傟傜傪夝偄偰丄丂俙亖侾侽/俁侾丂丄俠亖俀俇/俋俁
偟偨偑偭偰丄丂俥乮倶乯亖乮俁侽/俁侾乯倶2亄乮侾/俆乯倶亅俆/俁侾丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俉寧俀俈擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俉乯偺悢楍偺寛掕傕丄娭悢偺寛掕栤戣偱偁傠偆丅
栤戣丂丂幚悢偺悢楍乷倎n乸偑
丂丂倎3n亖倎n丂丄倎n+5亖倎n丂丄倎1亄倎2亄倎3亄倎4亄倎5亖係丂丄倎1倎3倎5亖俉
傪枮偨偡偲偒丄
乮侾乯丂倎1丄倎5 偺抣傪媮傔傛丅
乮俀乯丂悢楍偺榓 倎1亄倎2亄丒丒丒亄倎n 傪媮傔傛丅
乮夝乯乮侾乯丂倎3亖倎1丂丄倎6亖倎2丂丄倎6亖倎1 偐傜丄丂倎1亖倎2亖倎3
傑偨丄丂倎9亖倎3丂丄倎9亖倎4 偐傜丄丂倎1亖倎2亖倎3亖倎4
傛偭偰丄丂係倎1亄倎5亖係丂丄倎12倎5亖俉 偐傜丄丂倎12乮係亅係倎1乯亖俉
偡側傢偪丄丂倎13亅倎12亄俀亖乮倎1亄侾乯乮倎12亅俀倎1亄俀乯亖侽
倎1 偼幚悢側偺偱丄丂倎1亖亅侾丂偙偺偲偒丄丂倎5亖俉
乮俀乯丂倎n+5亖倎n丂傛傝丄悢楍乷倎n乸偼廃婜俆偱偁傞偺偱丄値亞侾 偲偟偰丄
丂値亖俆倠亄倰丂乮倠亖侽丄侾丄俀丄丒丒丒丂丄倰亖侽丄侾丄俀丄俁丄係乯丂偵懳偟偰丄
丂倎1亄倎2亄丒丒丒亄倎n亖係倠亅倰丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧侾俆擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俋乯偺栤戣傕丄婎杮栤戣偩傠偆丅
栤戣丂丂倎 傪惓偺掕悢偲偡傞丅俥乮倶乯亖倎倶亄佺01 俥2乮倲乯倓倲 傪傒偨偡娭悢俥乮倶乯偑偨偩侾偮偟偐
丂丂懚嵼偟側偄傛偆偵掕悢倎偺抣傪掕傔傛丅傑偨丄偦偺偲偒偺俥乮倶乯傪媮傔傛丅
乮夝乯丂佺01 俥2乮倲乯倓倲亖倐丂偲偍偔偲丄俥乮倶乯亖倎倶亄倐丂偱丄偙偺偲偒丄
倐亖佺01 乮倎倲亄倐乯2倓倲亖佺01 乮倎2倲2亄俀倎倐倲亄倐2乯倓倲亖倎2/俁亄倎倐亄倐2丂傛傝丄
丂倐2亄乮倎亅侾乯倐亄倎2/俁亖侽
戣堄傪枮偨偡偨傔偵偼丄偙偺倐偺俀師曽掱幃偑廳夝傪帩偰偽傛偄丅
丂敾暿幃傪俢偲偍偔偲丄丂俢亖乮倎亅侾乯2亅係倎2/俁亖侽丂偐傜丄丂倎2亄俇倎亅俁亖侽
丂倎亜侽偵拲堄偟偰丄丂倎亖亅俁亄俀
埲忋偐傜丄丂俥乮倶乯亖乮亅俁亄俀
乮捛婰乯丂椷榓俈擭俋寧俀俉擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮俀侽侽侽乯偺栤戣偼丄媡娭悢偵娭偡傞栤戣偱偁傞丅
栤戣丂丂幚悢 倎丄倐丄們丄倓 偑 倎倓亅倐們亗侽 傪枮偨偡偲偒丄娭悢 俥乮倶乯亖乮倎倶亄倐乯/乮們倶亄倓乯 偵
丂丂偮偄偰丄師偺栤偄偵摎偊傛丅
乮侾乯丂俥乮倶乯偺媡娭悢俥-1乮倶乯傪媮傔傛丅
乮俀乯丂俥-1乮倶乯亖俥乮倶乯 傪枮偨偟丄俥乮倶乯亗倶 偲側傞 倎丄倐丄們 丄倓 偺娭學幃傪媮傔傛丅
乮俁乯丂俥-1乮倶乯亖俥乮俥乮倶乯乯傪枮偨偟丄俥乮倶乯亗倶 偲側傞 倎丄倐丄們 丄倓 偺娭學幃傪媮傔傛丅
乮夝乯乮侾乯丂倷亖乮倎倶亄倐乯/乮們倶亄倓乯 偲偍偔偲丄丂乮們倷亅倎乯倶亖亅倓倷亄倐
丂偙偙偱丄丂們倷亅倎亖侽丂偲偍偔偲丄丂亅倓倷亄倐亖侽丂偡側傢偪丄丂倓倷亅倐亖侽丂偱丄
丂乮倎倓亅倐們乯倷亅倎倐亄倎倐亖侽丂偱丄倎倓亅倐們亗侽 傛傝丄丂倷亖侽
偙偺偲偒丄丂倎亖侽丂丄倐亖侽丂偐傜丄丂倎倓亅倐們亖侽丂偙傟偼丄忦審偵斀偡傞丅
丂傛偭偰丄丂們倷亅倎亗侽丂側偺偱丄丂倶亖乮亅倓倷亄倐乯/乮們倷亅倎乯
偟偨偑偭偰丄丂俥-1乮倶乯亖乮亅倓倶亄倐乯/乮們倶亅倎乯
乮俀乯丂俥-1乮倶乯亖俥乮倶乯 偐傜丄丂乮亅倓倶亄倐乯/乮們倶亅倎乯亖乮倎倶亄倐乯/乮們倶亄倓乯
傛偭偰丄丂乮倎亄倓乯乮們倶2亅乮倎亅倓乯倶亅倐乯亖侽乮
偙偙偱丄俥乮倶乯亗倶 傛傝丄丂倶亗乮倎倶亄倐乯/乮們倶亄倓乯 偐傜丄丂們倶2亅乮倎亅倓乯倶亅倐亗侽
傛偭偰丄丂倎亄倓亖侽
乮俁乯丂俥乮俥乮倶乯乯亖乮乮倎2亄倐們乯倶亄倐乮倎亄倓乯乯/乮們乮倎亄倓乯倶亄倐們亄倓2乯亖乮亅倓倶亄倐乯/乮們倶亅倎乯
偺暘曣傪暐偭偰惍棟偡傞偲丄丂乮倎2亄倎倓亄倐們亄倓2乯乮們倶2亅乮倎亅倓乯倶亅倐乯亖侽
乮俀乯傛傝丄丂們倶2亅乮倎亅倓乯倶亅倐亗侽丂側偺偱丄丂倎2亄倎倓亄倐們亄倓2亖侽丂丂乮廔乯
丂丂埲壓丄岺帠拞両