三垂線の定理 
有名なのに中々活躍の場がないと言われる「三垂線の定理」について、その応用をいろい
ろ探訪したいと思う。
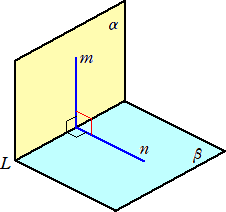
平面α上にない点Ｐから垂線を下し、その足をＨとする。Ｈを通らないα上の直線ＬにＨよ
り垂線を下し、その足をＱとする。
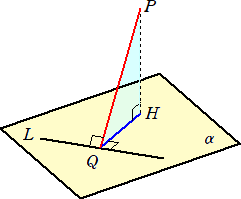
このとき、三垂線の定理は、次のことを主張するものである。
三垂線の定理 ＰＨ⊥α、ＨＱ⊥Ｌ ならば、 ＰＱ⊥Ｌ
定理の主張から分かるように、上図には、３つの垂線 ＰＨ⊥α、ＨＱ⊥Ｌ、ＰＱ⊥Ｌ がある。
三垂線の定理の系
（１） ＰＨ⊥α、ＰＱ⊥Ｌ ならば、 ＨＱ⊥Ｌ
（２） ＰＱ⊥Ｌ、ＨＱ⊥Ｌ で、ＰＨ⊥ＨＱ ならば、 ＰＨ⊥α
（定理の証明）
ＰＨ⊥α より、 ＰＨ⊥Ｌ よって、 平面ＰＱＨ⊥Ｌ より、 ＰＱ⊥Ｌ （終）
（系（１）の証明）
ＰＨ⊥α より、 ＰＨ⊥Ｌ よって、 平面ＰＱＨ⊥Ｌ より、 ＨＱ⊥Ｌ （終）
（系（２）の証明）
平面ＰＱＨ⊥Ｌ より、 ＰＨ⊥Ｌ ＨＱとＬで平面αが定まるので、 ＰＨ⊥α （終）
上記の結果から、 平面ＰＱＨ⊥平面α であることが分かる。
このような証明法を練習しよう。
問題 △ＡＢＣの垂心Ｈを通って△ＡＢＣに立てた垂線上の１点をＰとするとき、ＡＰ⊥ＢＣであ
ることを示せ。
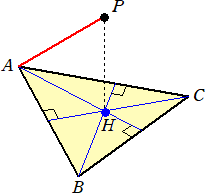
正射影をイメージすれば当たり前のことに見えるが、しっかり論証してみよう。
（解） ＡＨ⊥ＢＣ 、ＰＨ⊥ＢＣ より、 平面ＰＡＨ⊥ＢＣ よって、 ＡＰ⊥ＢＣ （終）
問題 四面体Ｏ-ＡＢＣにおいて、ＯＡ⊥ＡＢ、ＯＡ⊥ＯＣとする。
ＡＨ⊥△ＯＢＣのとき、ＯＨ⊥ＢＣが成り立つことを示せ。
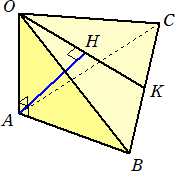
（解） ＯＡ⊥ＡＢ、ＯＡ⊥ＯＣより、 ＯＡ⊥△ＡＢＣ なので、 ＯＡ⊥ＢＣ
また、ＡＨ⊥△ＯＢＣ より、 ＡＨ⊥ＢＣ
よって、 △ＯＡＨ⊥ＢＣ なので、 ＯＨ⊥ＢＣ （終）
三垂線の定理をせっかく習ったので、上記の問題で三垂線の定理を用いてみよう。
（別解） ＡＯ⊥ＡＢ、ＡＯ⊥ＯＣより、 ＡＯ⊥△ＡＢＣ なので、 ＡＯ⊥ＢＣ
また、 ＡＨ⊥△ＯＢＣ なので、三垂線の定理より、 ＨＯ⊥ＢＣ （終）
（コメント） 三垂線の定理を用いてはみたものの、ほとんど解としては大差ない。もしかした
ら、三垂線の定理は知らなくても何とかなるレベルなのかな．．．？
（追記） 令和４年９月３日付け
次の性質は、正四面体の重要事項だろう。
正四面体ＡＢＣＤにおいて、Ｂより辺ＣＤに垂線ＢＭを下ろす。さらに、Ａより線分ＢＭに
垂線ＡＨを下ろす。このとき、
ＡＨ⊥△ＢＣＤ
が成り立つ。
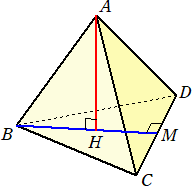
（補足） 上図で、Ｍは辺ＣＤの中点であり、Ｈは△ＢＣＤの重心で、ＢＨ：ＨＭ＝２：１ である。
（証明） 題意より、 ＢＭ⊥ＣＤ
また、△ＡＣＭ≡△ＢＣＭ より、 ＡＭ⊥ＣＤ
△ＡＢＭは、ＡＭ、ＢＭで定まるので、 △ＡＢＭ⊥ＣＤ
ＡＨは、△ＡＢＭ上の線分なので、 ＡＨ⊥ＣＤ
ＡＨ⊥ＢＭ、ＡＨ⊥ＣＤ で、△ＢＣＤは、ＢＭ、ＣＤで定まるので、 ＡＨ⊥△ＢＣＤ （終）
（コメント） 証明から分かるように、四面体ＡＢＣＤが正四面体であることは本質的でない。
△ＡＣＭ≡△ＢＣＭが言える四面体が持つ性質である。
三垂線の定理を用いれば、次のように示される。
（別解） 題意より、 ＢＭ⊥ＣＤ で、△ＡＣＭ≡△ＢＣＭ より、 ＡＭ⊥ＣＤ
ＨＭ⊥ＣＤ で、ＡＨ⊥ＨＭ なので、三垂線の定理より、 ＡＨ⊥△ＢＣＤ （終）
（追記） 令和４年９月４日付け
２平面が垂直を示すには、２平面の交線に垂直な各平面上の直線のなす角が９０°を示
せばよい。
ここで、次の驚愕の公式が成り立つ。
∠ＰＯＨ＝α、∠ＨＯＱ＝β、∠ＰＯＱ＝γとするとき、
 |
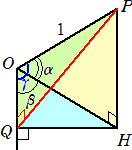△ＯＰＨ⊥△ＯＱＨ であるための必要十分条件は、
ｃｏｓα・ｃｏｓβ＝ｃｏｓγ
である。 |
証明は、三垂線の定理から明らかだろう。
∠ＰＨＯ＝９０°、∠ＨＱＯ＝９０°で、 ｃｏｓα・ｃｏｓβ＝ｃｏｓγ のとき、∠ＰＱＯ＝９０°
このとき、ＱＯ⊥ＰＱ、ＱＯ⊥ＨＱ より、 ＱＯ⊥△ＰＱＨ なので、ＱＯ⊥ＰＨ
よって、ＰＨ⊥△ＯＱＨ となり、その結果として、△ＯＰＨ⊥△ＯＱＨ であることが分かる。
この話題に関連して、練習問題を置いておこう。
問題 ＯＡ＝４、ＡＢ＝６、ＯＣ＝ＡＣ＝４
、∠ＢＡＣ＝６０°、∠ＯＡＢ＝４５°である四面体
Ｏ-ＡＢＣの体積を求めよ。
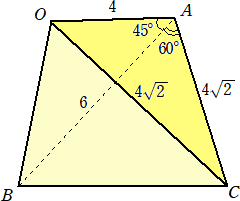
（解） cos４５°＝１/、ｃｏｓ６０°＝１/２ である。また、△ＯＡＣにおいて、余弦定理より、
ｃｏｓ∠ＯＡＣ＝（１６＋３２−３２）/３２＝１/（２）
である。このとき、 cos４５°ｃｏｓ６０°＝１/（２）＝ｃｏｓ∠ＯＡＣ が成り立つ。
よって、 △ＯＡＢ⊥△ＡＢＣ である。
したがって、△ＡＢＣを底面とする四面体Ｏ-ＡＢＣの高さは、 ４ｓｉｎ４５°＝２
△ＡＢＣ＝（１/２）・６・４・ｓｉｎ６０°＝６
なので、
四面体Ｏ-ＡＢＣの体積は、 （１/３）・６・２＝８
（終）
（追記） 令和４年９月６日付け
京都大学前期理系（２０１６）で、次のような空間図形の問題が出題されている。問題は
一部改題しました。
問題 四面体OABCの頂点A、B、Cからそれぞれの対面へ下ろした垂線が対面の外心を通
るとき、四面体OABCは正四面体であることを示せ。
（解） 題意より、 ＡＢ＝ＡＣ＝ＯＡ 、ＡＢ＝ＢＣ＝ＯＢ 、ＢＣ＝ＡＣ＝ＯＣ なので、
ＡＢ＝ＢＣ＝ＡＣ＝ＯＡ＝ＯＢ＝ＯＣ が成り立つ。
よって、四面体OABCは正四面体である。 （終）
（コメント） 京都大学理系の問題と聞くと、思わず身構えてしまうが、気楽に考えれば解け
るであろう平易な問題である。ただ、空間図形の問題なので、空間把握が出来な
い人には難しいかもしれない。
（追記） 令和４年９月１０日付け
上記の京都大学の問題では、正四面体特有の性質のように錯覚させられるが、四面体
Ｏ-ＡＢＣにおいて、頂点Ｏより△ＡＢＣに下ろした垂線の足が△ＡＢＣの外心となるためには
ＯＡ＝ＯＢ＝ＯＣ
という性質が本質的である。この「ＯＡ＝ＯＢ＝ＯＣ」という条件があれば、垂線の足Ｈについ
て、
ＨＡ＝ＨＢ＝ＨＣ
が成り立ち、Ｈは△ＡＢＣの外心であることが分かる。
この話題に関して、次の練習問題を残しておこう。
問題 四面体Ｏ-ＡＢＣにおいて、ＯＡ＝ＯＢ＝ＯＣ＝７ で、ＡＢ＝３、ＢＣ＝５、ＣＡ＝７ と
するとき、四面体Ｏ-ＡＢＣの体積を求めよ。
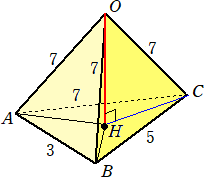
（解） 頂点Ｏより、底面の△ＡＢＣに垂線ＯＨを下ろすと、点Ｈは△ＡＢＣの外心である。
△ＡＢＣにおいて、 ｓ＝（３＋５＋７）/２＝１５/２ なので、ヘロンの公式より、
△ＡＢＣ＝√｛（１５/２）（９/２）（５/２）（１/２）｝＝（１５/４）
よって、△ＡＢＣの外接円の半径をＲとすると、 Ｒ＝３・５・７/｛４（１５/４）｝＝７/
したがって、 ＯＨ2＝４９−４９/３＝４９・（２/３） より、 ＯＨ＝（７/３）
以上から、
四面体Ｏ-ＡＢＣの体積＝（１５/４）×（７/３）×（１/３）＝（３５/４） （終）
（追記） 令和４年９月８日付け
三垂線の定理を用いる問題を創作してみた。
問題 ＯＡ⊥△ＡＢＣの四面体Ｏ-ＡＢＣにおいて、ＯＢ＝７、ＡＢ＝４、ＢＣ＝ＣＡ＝８とする。
Ａより、辺ＢＣに垂線ＡＤを引く。このとき、線分ＯＤの長さを求めよ。
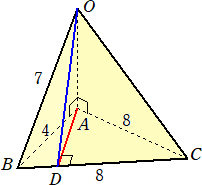
（解） ｃｏｓ∠ＡＢＣ＝２/８＝１/４ なので、 ＢＤ＝４ｃｏｓ∠ＡＢＣ＝１ である。
また、三垂線の定理より、 ∠ＯＤＢ＝９０°なので、三平方の定理より、
ＯＤ2＝７2−１2＝４８ すなわち、 ＯＤ＝４ （終）
（追記） 令和４年９月９日付け
問題 立方体ＡＢＣＤ-ＥＦＧＨにおいて、対角線ＥＧとＦＨの交点をＯとする。
 |
このとき、次を示せ。
（１） ＡＯ⊥ＦＨ
（２） ＡＧ⊥ＢＤ |
（解）（１） ＡＥ⊥正方形ＥＦＧＨ 、 ＥＯ⊥ＦＨ なので、三垂線の定理より、 ＡＯ⊥ＦＨ
（２） ＡＥ⊥正方形ＡＢＣＤ より、ＡＥ⊥ＢＤ で、 ＢＤ⊥ＥＧ より、 ＢＤ⊥△ＡＥＧ
よって、 ＡＧ⊥ＢＤ （終）
この手の問題は、ベクトルを用いれば余り考えずに機械的に解くことが出来る。
（別解） 立方体ＡＢＣＤ-ＥＦＧＨの１辺の長さが２とすると、Ａ（２，０，２）、Ｂ（２，２，２）、
Ｃ（０，２，２）、Ｄ（０，０，２）、Ｅ（２，０，０）、Ｆ（２，２，０）、Ｇ（０，２，０）、Ｈ（０，０，０）
このとき、 Ｏ（１，１，０） である。
（１） ＡＯ＝（−１，１，−２） 、ＦＨ＝（−２，−２，０） なので、
ＡＯ・ＦＨ＝２−２＋０＝０ より、 ＡＯ⊥ＦＨ
（２） ＡＧ＝（−２，２，−２） 、ＢＤ＝（−２，−２，０） なので、
ＡＧ・ＢＤ＝４−４＋０＝０ より、 ＡＧ⊥ＢＤ （終）
以下、工事中！