以前、入試の採点をしているとき、「ターレスの定理より、・・・」と論述している受験生の答
案があり、採点官の間でしばし話題になった。
ターレス(B.C.624頃〜B.C.548頃)は、現在のトルコにあるミレトス出身の数学者であり哲学
者で、定理を提唱し、それを証明するという抽象数学の元祖と言われる。その頃、日本は弥
生時代で、ターレスの偉大さが実感できる。ターレスは、タレスとかタレースとも呼ばれる。
ギリシャ七賢人の一人に上げられ、「汝自身を知れ」という有名な格言を残している。三平
方の定理で有名なピュタゴラスはターレスの教え子らしい。
ターレスは、今では当たり前と思われる定理をいくつか提起している。
(1) 切片定理 △ABCの辺AB、AC上に点D、Eをとり、DEとBCは平行とする。
このとき、 DE/BC=AD/AB=AE/AC
※ これは、ターレスが導いた最初の定理で、今でいうところの「平行線の公理」なるもので
ある。
(2) 三角形の内角の和は180°である。
(3) 2等辺三角形の両底角は等しい。
(4) 円は直径により2等分される。
(5) 同じ直線上にない任意の3点を通る円がただ一つ存在する。(外接円の存在)
(6) 外接円の直径は、内接する直角三角形の斜辺と一致する。
(7) 交差する2直線の対頂角は等しい。
(8) 円周角の定理 一つの弧に対する円周角は等しく、中心角の半分である。
(9) 直径に対する円周角は、直角である。(→ 参考:「ターレスの定理」)
世間一般では、「ターレスの定理」というと、この(9)を指すことが多いと推察されるが、上
記で列挙したように、ターレスはいくつかの定理を残しているので、冒頭の受験生のように
突然「ターレスの定理より、・・・」といわれても困るわけである。結果とその理由付けが両方
出来ている場合に加点する仕組みなので、一応審議対象となった次第である。
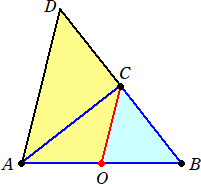
(9)について、ターレスは次のような証明を行ったらしい。