２次関数 Ｆ（ｘ）＝ａｘ2＋ｂｘ＋ｃ のグラフから、係数 ａ 、ｂ 、ｃ の符号を決定する問題は、
古くから存在するよく知られた問題である。
たとえば、２次関数のグラフが左下図のように与えられたものとする。
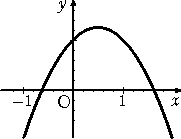このとき、 上に凸なので、 ａ＜０軸 ｘ＝−ｂ/２ａ＞０ と ａ＜０ から、 ｂ＞０
ｙ 切片 ｙ＝ｃ から、 ｃ＞０
と、直ちに符号は決定される。
上図からは、更に、
ａ＋ｂ＋ｃ＞０ 、 ａ−ｂ＋ｃ＜０ 、 ｂ2−４ａｃ＞０
などもうかがい知れる。
上記の計算では、ｂ の符号の計算が一番複雑だが、微分を知っていれば、次のように簡
単に求められる。
すなわち、 Ｆ’（ｘ）＝２ａｘ＋ｂ より、 Ｆ’（０）＝ｂ は、ｙ 軸との交点における接線の傾き
なので、グラフより明らかに、 ｂ＞０ である。
この符号の決定問題で ３次関数の場合が、日本大学 文理学部（２００８）で出題されたこ
とを最近知った。
日本大学 文理学部（２００８）
下の図は、３次関数 Ｆ（ｘ）＝ａｘ3＋ｂｘ2＋ｃｘ＋ｄ のグラフである。以下の問いに答えよ。
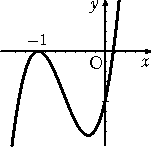（１） ａ 、ｄ 、ｃ の符号を判定せよ。（２） ｃ 、ｄ を、 ａ 、ｂ を用いて表せ。
（３） ｂ の符号を判定せよ。
（４） ０ 、ａ 、ｂ 、ｃ 、ｄ を小さい順に並べよ。 （一部改題）
（解）（１） ｘ → ∞ のとき、 Ｆ（ｘ） → ∞ なので、 ａ＞０ である。
ｙ 切片 ｙ＝ｄ から、 ｄ＜０ である。
Ｆ’（ｘ）＝３ａｘ2＋２ｂｘ＋ｃ より、 Ｆ’（０）＝ｃ は、ｙ 軸との交点における接線の
傾きなので、グラフより明らかに、 ｃ＞０ である。
（２） Ｆ’（−１）＝０ より、 ３ａ−２ｂ＋ｃ＝０ なので、 ｃ＝２ｂ−３ａ
Ｆ（−１）＝０ より、 −ａ＋ｂ−ｃ＋ｄ＝０ なので、 ｄ＝ａ−ｂ＋ｃ＝ｂ−２ａ
（３） ２ｂ＝３ａ＋ｃ＞０ より、 ｂ＞０
（４） ｄ＜０ より、 ｂ−２ａ＜０ である。
このとき、 ｃ−ａ＝２（ｂ−２ａ）＜０ より、 ｃ＜ａ である。
また、 ２ｂ＝３ａ＋ｃ で、 ａ＞０ 、 ｃ＞０ より、 ２ｂ＞２ａ 即ち、 ｂ＞ａ
以上から、 ｄ＜０＜ｃ＜ａ＜ｂ である。 （終）
（コメント） （３）で、ｂ の符号を判定するとき、Ｆ（ｘ）が、ｘ＝−１ で極値をとることを用いて
いるが、これは本質的ではない。
グラフから、Ｆ（ｘ）は、ｘ＝０ の周辺で下に凸なので、Ｆ”（ｘ）＝６ａｘ＋２ｂ より、
Ｆ”（０）＝２ｂ＞０ である。よって、 ｂ＞０ である。
以上から、３次関数においても、グラフが与えられれば、その係数の符号を決定すること
ができる。
（追記） 上記の考え方は、４次関数でも適用できる。
例えば、４次関数 Ｆ（ｘ）＝ａｘ4＋ｂｘ3＋ｃｘ2＋ｄｘ＋ｅ のグラフが下図であるとき、ａ 、ｂ 、
ｃ 、ｄ 、ｅ の符号を決定してみよう。
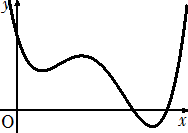
（解） ｘ → ∞ のとき、 Ｆ（ｘ） → ∞ なので、 ａ＞０ である。
ｙ 切片 ｙ＝ｅ から、 ｅ＞０ である。
Ｆ’（ｘ）＝４ａｘ3＋３ｂｘ2＋２ｃｘ＋ｄ より、 Ｆ’（０）＝ｄ は、ｙ 軸との交点における接線の
傾きなので、グラフより明らかに、 ｄ＜０ である。
Ｆ”（ｘ）＝１２ａｘ2＋６ｂｘ＋２ｃ より、 Ｆ”（０）＝２ｃ で、ｘ＝０ の周辺で下に凸であること
から、 ２ｃ＞０ すなわち、 ｃ＞０ である。
一番難しそうなのが ｂ の符号であるが、次のように考えれば即答だろう。
グラフから、ｙ＝Ｆ（ｘ）と直線 ｙ＝ｐｘ＋ｒ が ｘ＞０で４点で交わるように出来る。
解と係数の関係から、 −ｂ/ａ＞０ で、ａ＞０ より、 ｂ＜０ である。 （終）