正８角形で遊ぶ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　今、１辺が２の正８角形ＡＢＣＤＥＦＧＨがある。点Ｏはその中心である。

　　　

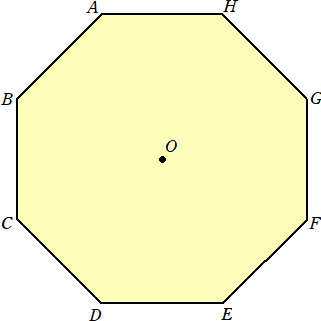
　正８角形の一つの内角の大きさは、　６×１８０°÷８＝１３５°である。したがって、
１辺の長さが２＋２の正方形に４辺（ＢＣ、ＤＥ、ＦＧ、ＨＡ）を接して、スッポリ収まる。

　このことから、１辺が２の正８角形ＡＢＣＤＥＦＧＨの面積は、

　　（２＋２）²−²÷２×４＝１２＋８−４＝８＋８

　ＯＡ＝Ｒ とおくと、面積の計算から、　

　　（１/２）Ｒ²・ｓｉｎ４５°×８＝２Ｒ²＝８＋８　より、　Ｒ²＝４＋２

よって、正８角形の外接円の半径Ｒについて、　Ｒ＝√（４＋２）

＃ （２Ｒ）²＝１２＋８＋２²＝１６＋８ から、Ｒ＝√（４＋２） としても求められる。

　また、正８角形の内接円の半径を ｒ とすると、　ｒ ＝Ｒｃｏｓ２２．５°である。

　ここで、　ｃｏｓ²２２．５°＝（１＋ｃｏｓ４５°）/２＝（２＋）/４　なので、

　ｒ² ＝Ｒ²ｃｏｓ²２２．５°＝（４＋２）（２＋）/４＝３＋２　より、　ｒ＝１＋

＃正８角形の内接円の半径は、２重根号のない綺麗な形で求まるんですね！もっとも、上記
　のような計算をしなくても、

　　２ｒ＝２＋２　から、直ちに、　ｒ＝１＋　と求まりましたね！

　正８角形に下図のように円が内接している。

　　　

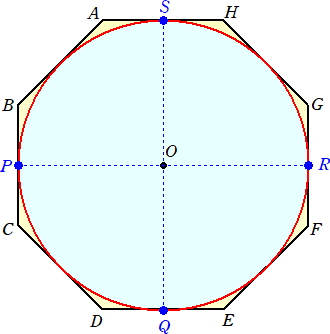
　Ｐ、Ｑ、Ｒ、Ｓはその接点で、それぞれ辺ＢＣ、ＤＥ、ＦＧ、ＨＡの中点でもある。

　次に、正８角形と同じ面積を持つ正方形を作りたい。トレバーが創案したと言われる、次の
ような方法が知られている。

　　　

　直径ＰＲに対して、円周上にＲＵ＝２（正８角形の１辺の長さ）となる点Ｕをとる。

　次に、線分ＰＵに垂線ＱＶを下ろす。また、線分ＱＶに垂線ＲＷを下ろす。

　線分ＷＲ上にＷＸ＝２となる点Ｘをとる。線分ＶＵ上に、ＶＹ＝２となる点Ｙをとる。

　このとき、正８角形の中央に、１辺の長さが２（＝正８角形の１辺の長さ）の正方形ＶＷＸＹ
ができる。

　下図のように、正方形１個と４個の合同な５角形に、正８角形が分解される。

　これらを組み合わせると、実は、正方形が一つ出来る。

　　　

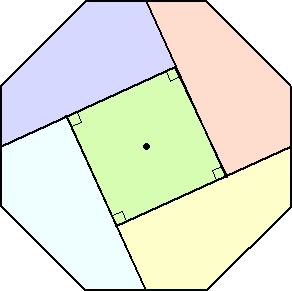
が、次の正方形になるとは．．．。まさに、アンビリーバブルですね！

　　　

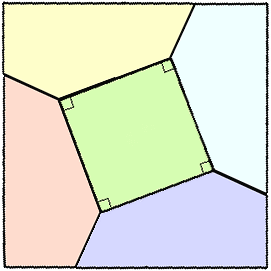
　正８角形の辺の長さを２とする。上図から、出来た正方形の１辺の長さは、

　　ＰＹ＋ＸＲ＝ＰＵ

で、　ＰＵ²＝ＰＲ²−ＵＲ²＝（２＋２）²−２²＝８＋８　から、上記の結果：

　１辺が２の正８角形ＡＢＣＤＥＦＧＨの面積は、８＋８

と一致する。


　　以下、工事中！