丸い地球を平面上に表現する技法はたくさんあるが、長方形を使うもので最も馴染みが
あるのは、「メルカトル図法」だろう。
近代地図学の祖と言われるメルカトル（Ｇｅｒａｒｄｕｓ Ｍｅｒｃａｔｏｒ 1512〜1594）が１５６９
年にオランダで発表した世界地図に使った技法として知られている。ただ、それ以前にも
この技法を用いた人はいたらしい。
このメルカトル図法は、経線に対して等角に直線上を進むと目的地に到達できるという
利点があり、船の航行のための航路図として利用されている。ただし、この航路は最短
航路を表すものではなく、最短航路を表すものは、大圏航路と言われる。これは、出発点
と到着点を通る大円（球の中心を通る平面で球面を切ったときの切り口の円）に沿う航路
である。
メルカトル図法は、赤道で地球に接する円筒面に地図を投影することにより得られる。
経線と緯線が直交するという特徴があり、北極、南極といった極周辺では、地図上の距
離や面積は無視され、限りなく無限大になってしまうという欠点がある。有効範囲は、だ
いたい上下８５°くらいらしい。
メルカトル図法の数学理論は、１５９９年にイギリスのライト（Ｅ．Ｗｒｉｇｈｔ）が明らかにした
らしい。どのような理論か大いに興味があるところである。
標準子午線と赤道を基準として、経度を α 、緯度を β とすると、地球上の各点は、座標
（ α ， β ）で表される。ただし、−１８０°≦ α ≦ １８０°、−９０°≦ β ≦ ９０°である。
球面座標系で考えれば、空間において、
ｘ＝ｒ・ｃｏｓβｃｏｓα 、 ｙ＝ｒ・ｃｏｓβｓｉｎα 、 ｚ＝ｒ・ｓｉｎβ （ｒ は、地球の半径）
であるが、ここでは上記の（ α ， β ）で平面的に座標を考えることにする。
赤道で地球に接する円筒面に地図を投影するとき、地球上の点（ α ， β ）が、地図上の
点（ ｘ ， ｙ ）に写されるものとする。
地球の半径を １ として、単純に考えれば、 ｘ ＝ α 、 ｙ ＝ ｔａｎ β であるが、メルカト
ル図法は、平行な緯線の書き方に一工夫を加えているところが面白い。
実際の投影の媒介変数表示は、
である。
このような式になる理由は、メルカトル図法が地図上の２点に対して、常に経線に対して
等角に進めばよいようにすることを目指したためである。
上記の媒介変数表示を導いてみることにしよう。
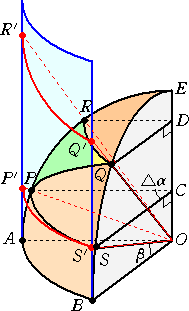左図において、Ｏ を地球の中心、弧ＡＢを赤道の一部とする。
Ａ（ α ， ０ ）、Ｂ（ α＋Δα ， ０ ）、Ｐ（ α ， β ）
Ｑ（ α＋Δα ， β＋Δβ ）、Ｒ（ α ， β＋Δβ ）
Ｓ（ α＋Δα ， β ）
とする。４点Ｐ、Ｑ、Ｒ、Ｓは、赤道で地球に接する円筒面
にそれぞれ点Ｐ’、Ｑ’、Ｒ’、Ｓ’に投影されるものとする。
Δα が十分小なるとき、面ＡＢＯ、面ＰＳＣ はそれぞれ
△ＡＢＯ、△ＰＳＣ と見なされ、
△ＡＢＯ∽△ＰＳＣ
であると言える。
このとき、 ＰＳ/ＡＢ＝ＳＣ/ＢＯ＝ＳＣ/ＳＯ＝ｃｏｓβ なので、 ＰＳ＝ＡＢ・ｃｏｓβ
同様にして、 ＲＱ＝ＡＢ・ｃｏｓ（β＋Δβ） が成り立つ。
また、 ＡＢ＝Ｐ’Ｓ’ と見なしてよいので、 ＰＳ＝Ｐ’Ｓ’・ｃｏｓβ から、
Ｐ’Ｓ’＝ＰＳ・ｓｅｃβ
が成り立つ。 さらに、Δβ が十分小なるとき、球面上の面ＰＱＲ は、∠ＰＲＱ＝９０°の直角
三角形ＰＱＲ と見なせる。
ＡＢ＝Δα なので、 ＲＱ＝△α・ｃｏｓ（β＋Δβ） となる。
経線に対して、角θの方向に進行するものとすると、 ∠ＱＰＲ＝θ と見なせる。
このとき、
であると言える。 Δα→０ 、Δβ→０ として、
が得られる。 よって、ｔａｎθ＝定数 として考えると、
と書ける。
赤道で地球に接する円筒面に地図を投影するとき、地球上の点（ α ， β ）が、地図上の
点（ ｘ ， ｙ ）に写されるものとし、さらに、地図上の２点に対して、常に経線に対して等角に
進めばよいようにするためには、地球の半径を １ として、投影の媒介変数表示を、
とすればよいことが上式より導かれる。
ここで、
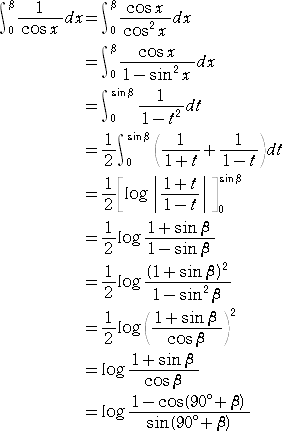
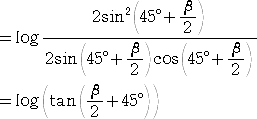
なので、媒介変数表示は、
で与えられることが示された。
実際に、この関数に従い緯線を描いてみると下図のようになる。
（コメント） 今まで何となく見てきた世界地図の緯線について、このような数理があったとは
驚きです。緯線て、怪しげな幅で引かれているわけだが、これでスッキリですね！