格子点　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　

　平成２０年９月１２日付けで当ＨＰの掲示板「出会いの泉」に、ＨＮ「空港」さんが、次のよう
な問いかけをされた。中学１年で、このような問題意識を持たれていることに驚きました。

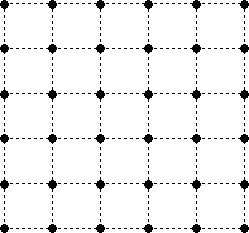
　　　ある本で、

　　『 ｘｙ平面上において格子点を結んで出来る

　　正Ｎ角形は、Ｎ＝4、つまり、正方形のときに

　　限る。』

　　的なことが書いてあったんですが、これはど

　　うやって説明できるのでしょうか？




　この問題に対して、当ＨＰがいつもお世話になっているらすかるさんが明解に説明された。
（多少文言を補充させていただきました。）

Ｎ＝４ のとき、明らかに正方形（正４角形）を作ることができる。

Ｎ＝３ のとき、一辺の長さが ａ の正３角形の面積は、 ａ²/４ で、ａ² は有理数より、面

　　　　　　　　積は必ず無理数となる。格子点を結ぶ多角形の面積は必ず有理数であるの

　　　　　　　　で、これは矛盾である。

Ｎ＝６ のとき、正６角形が作れるものとすると、頂点を一つおきにとって正３角形を作るこ

　　　　　　　　とが出来る。しかるに、これは不可能である。

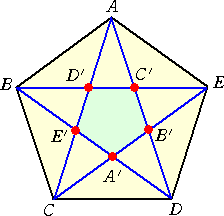
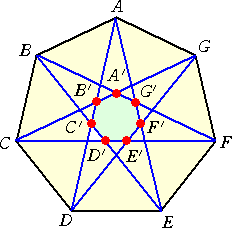
Ｎ＝５、Ｎ≧７ のとき、正Ｎ角形が作れるものとして、頂点を２つ飛ばしで結ぶと、内側に頂

　　　　　　　　点が格子点である正Ｎ角形を作ることができる。

　　例えば、Ｎ＝５ のとき、正５角形ＡＢＣＤＥにおいて、

	四角形ＡＢＡ’Ｅは平行四辺形で、Ａ、Ｂ、Ｅ が格子 　点であることから、Ａ’も格子点である。 　同様にして、Ｂ’、Ｃ’、Ｄ’、Ｅ’も格子点である。 　　このとき、５角形Ａ’Ｂ’Ｃ’Ｄ’Ｅ’は格子点を頂点に 　持つ正５角形となる。 　　この操作を続けると、正５角形ＡＢＣＤＥの内部に 　格子点を頂点に持つ、いくらでも小さい正５角形が
	作れることになる。しかるに、これは矛盾である。

　　　　　　Ｎ＝７ のときも作れないことは下図から明らかだろう。


　　四角形ＡＢＡ’Ｇが平行四辺形から、Ａ’も格子点で

　あるので、Ｎ＝５ の場合と同様にして示される。

　　　　　　よって、Ｎ≧７ のとき、正Ｎ角形が作れるものとして、頂点を２つ飛ばしで結ぶと、

　　　　　内側に頂点が格子点である正Ｎ角形を作ることができる。この操作を続けることに

　　　　　より矛盾を得ることが出来る。

（コメント）　頂点を２つ飛ばしで考えると平行四辺形が出来るんですね！今まで経験のない
　　　　　　証明の仕方でした。らすかるさんに感謝します。