
曲線 y=1/x (x≧1) のグラフを x 軸のまわりに回転させてできる図形は、ガブリエルの
ラッパ または、ガブリエルのホルン と呼ばれる。
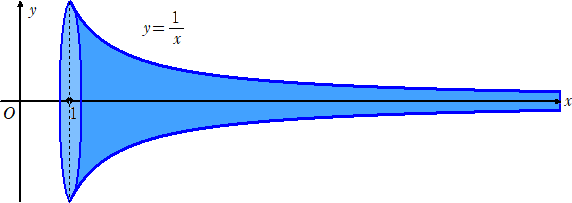
この立体図形は、有限の体積を持ちながら、表面積は無限という特徴を持つので有名で
ある。
実際に、体積Vは、V=π∫1∞ (1/x2)dx=π[−1/x]1∞=π (有限確定値) であるの
に対して、表面積Sは、
S>2π(1/2)・1+2π(1/4)・2+・・・=π(1+1+・・・) → ∞
より、 Sは、無限大に発散してしまう。
(コメント) 有限な体積を持ちながら、表面積は無限とは、面白いですね!
以下、工事中!