６０度の魔力　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　６０度の角を持つ図形と言えば、直ぐに正三角形を想起される方が多いだろう。

　最近、６０度の角を持つ三角形について種々の経験をしたので備忘録としてまとめておこ
うと思う。

（１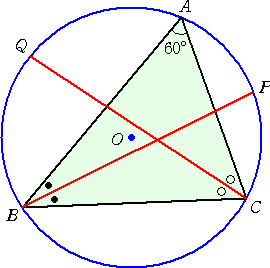）	∠Ａ＝６０°の△ＡＢＣが円Ｏに接している。 　∠Ｂ、∠Ｃの２等分線が円Ｏと交わる点を 　それぞれＰ、Ｑとおく。 　　このとき、ＢＰ＝ＣＱが成り立つ。

　この事実は、△ＡＢＣが正三角形ならば自明であるが、そうでなくとも成り立つというところ
が面白い。

（証明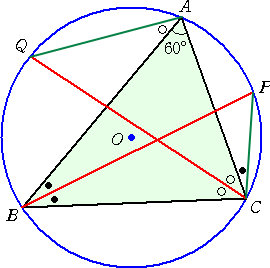）	左図において、　∠Ｂ＋∠Ｃ＝１２０°なので、 　　　∠ＡＢＰ＋∠ＡＣＱ＝６０° 　　円周角の定理より、　∠ＡＢＰ＝∠ＡＣＰ 　　よって、　∠ＰＣＱ＝６０°　である。 　　さらに、円周角の定理より、 　　　∠ＱＡＢ＝∠ＱＣＢ 　　なので、　∠ＱＡＣ＝∠ＰＣＢ　が成り立つ。 　　したがって、　ＢＰ＝ＣＱ　　（証終）

（コメント）　円周角の大きさが等しいので弦の長さも等しいというのは、当たり前と言えば
　　　　　　当たり前ですが、証明法としては斬新ですね！


（追記）　Ｈ．Ｎａｋａｏ さんから別証をいただきました。（令和７年１１月３０日付け）

　２つの正三角形ができることに着目すると、以下のように証明できます。

[証明]　CQとBPの交点をRとする。円周角は等しいので、∠RPC＝∠RQB＝６０°

　∠ACP=∠ABP　より、

　∠RCP＝∠RCA+∠ACP＝∠RCA+∠ABP＝(∠B＋∠C)/２＝６０°　である。

△RPCは２つの角が６０°なので、正三角形である。よって、RC＝RP である。

同様に、△RBQも正三角形であるので、BR＝QR である。

従って、BP＝BR＋RP＝QR＋RC＝CQ　である。　　（証終）

（２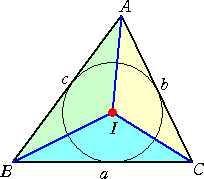）	左図の△ＡＢＣにおいて、内心を Ｉ とする。 　△ＡＢＩ＋△ＡＣＩ＝２△ＢＣＩ　が成り立つとき、∠Ａの 　最大値は、６０°であることを示せ。

　　この等式も、△ＡＢＣが正三角形ならば自明であるが、実は、正三角形に限るという点
が自明ながら興味深い。

（証明）　△ＡＢＣの内接円の半径を ｒ とすると、　△ＡＢＩ＋△ＡＣＩ＝２△ＢＣＩ　より、

　ｂｒ/２＋ｃｒ/２＝２×ａｒ/２　なので、　ａ＝（ｂ＋ｃ）/２　がなりたつ。

このとき、余弦定理より、

　

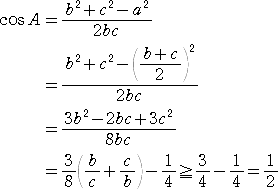
０°＜Ａ＜１８０°なので、　０°＜Ａ≦６０°より、∠Ａの最大値は、６０°である。

しかも、等号が成り立つのは、ｂ＝ｃ のときに限るので、△ＡＢＣは正三角形となる。（証終）


（追記）　令和７年１１月２９日付け

　次の東北大学　前期文系（２００３）の問題は、基本的な問題である。

問題　　 △ABCにおいて、ＡＢ＝１、ＡＣ＝２、∠Ａ＝６０°とする。正の数ｍ、ｎに対し、
　　辺ＢＣ、ＣＡ、ＡＢを ｍ ： ｎ の比に内分する点を順にＤ、Ｅ、Ｆとする。
（１）　ＤＥとＥＦが垂直であるときの比 ｍ ： ｎ を求めよ。
（２）　どのような正の整数ｍ、ｎに対しても、ＡＤとＥＦは垂直でないことを示せ。

（解）（１）　ＡＢ＝ａ、ＡＣ＝ｂ　とおくと、ａ・ｂ＝１・２・ｃｏｓ６０°＝１

　ＡＤ＝（ｎａ＋ｍｂ）/（ｍ＋ｎ）　、ＡＥ＝ｎｂ/（ｍ＋ｎ）　、ＡＦ＝ｍａ/（ｍ＋ｎ）

ＤＥ＝ＡＥ−ＡＤ＝｛（−ｎ）ａ＋（ｎ−ｍ）ｂ｝/（ｍ＋ｎ）　、ＥＦ＝（ｍａ−ｎｂ）/（ｍ＋ｎ）　より、

ＤＥ・ＥＦ＝（−ｍ²＋４ｍｎ−３ｎ²）/（ｍ＋ｎ）²＝０　から、　ｍ²−４ｍｎ＋３ｎ²＝０

よって、　（ｍ−ｎ）（ｍ−３ｎ）＝０　より、　ｍ＝ｎ　、３ｎ

したがって、　ｍ ： ｎ＝１ ： １　、ｍ ： ｎ＝３ ： １

（２）　ＡＤ・ＥＦ＝（ｍ²−３ｍｎ−ｎ²）/（ｍ＋ｎ）²＝０　と仮定すると、　ｍ²−３ｍｎ−ｎ²＝０

ｍ、ｎ は正の整数なので、　ｍ/ｎ＝（３＋）/２　すなわち、　（２ｍ−３ｎ）/ｎ＝

は無理数なので、これは矛盾である。

よって、どのような正の整数ｍ、ｎに対しても、ＡＤとＥＦは垂直でない。　　（終）



　　以下、工事中！