物理の問題に親しむ　　　　　　　　　　　　　　　　　　　　　　　　　

　私の高校のときの担任の先生が物理の先生で、週８時間、相当鍛えられた。夏休みも物
理の実験に明け暮れ、その頃がとても懐かしい。そんなわけで徒然なるままに関心の趣くま
まに物理の問題に取り組んでいこうと思う。

問題１（反射の法則）

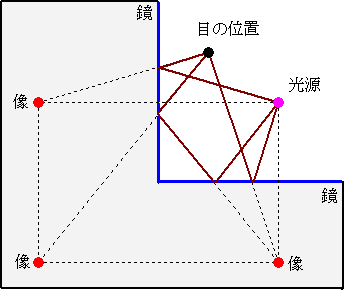
　２枚の鏡を直角にして向かい合わせ、この間に光源を置いたら、その像はどこにできるか？

（解）
　　　

問題２（球面鏡の一般公式：１/ａ＋１/ｂ＝１/ｆ　　光源までの距離ａ、像までの距離ｂ、焦点距離ｆ）

　焦点距離３０ｃｍの凹面鏡の前方１０ｃｍにある光源の像の位置を求め、実像か虚像か求
めよ。

（解）　１/１０＋１/ｂ＝１/３０　より、　ｂ＝−１５　　よって、凹面鏡の後方１５ｃｍの位置に

　　　虚像を生ずる。

問題３（像の倍率と正立・倒立の公式　ｍ＝−ｂ/ａ　ｍ＞０ のとき正立、ｍ＜０ のとき倒立）

　凸面鏡による像は必ず正立し、元の物体より小さくなることを示せ。

（解）　１/ａ＋１/ｂ＝１/ｆ　から、　ｂ＝ａｆ/（ａ−ｆ）　これを、ｍ＝−ｂ/ａ　に代入して、

　　　ｍ＝−ｆ/（ａ−ｆ）

　　題意より、　ａ＞０、ｆ＜０　であるので、　ｍ＞０　となる。よって、像は必ず正立。

　　さらに、　ｍ＜１　なので、像は元の物体より小さくなる。

問題４　自動車のバックミラーに凸面鏡が用いられるのはなぜか？

（解）　視野が広くなるから。

問題５（レンズの公式：１/ａ＋１/ｂ＝１/ｆ　　光源までの距離ａ、像までの距離ｂ、焦点距離ｆ）

　焦点距離３０ｃｍの凸レンズの前方６０ｃｍに光源を置き、凸レンズの後方２０ｃｍに焦点
距離３０ｃｍの凹レンズを置く。像はどこにできるか。

（解）　凹レンズがなかったとすれば、　１/６０＋１/ｂ＝１/３０　より、　ｂ＝６０　　よって、凸

　　レンズの後方６０ｃｍの位置に像を生ずる。実際は、途中凹レンズがあるので、

　　１/（−４０）＋１/ｂ＝１/（−３０）　より、　ｂ＝−１２０

　　よって、凸レンズの前方１００ｃｍに虚像ができる。

問題６　重さＷｋｇｗの一様な太さの棒の両端Ａ、Ｂに丈夫な糸をつけて吊したら、下図のよ
　　　　うにＡ端の糸は水平と６０°、Ｂ端の糸は水平と３０°傾いて釣り合った。糸の引っ張
　　　　りの張力Ｔ_Ａ、Ｔ_Ｂおよび棒の傾きの角θを求めよ。

　　　

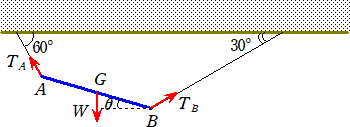
（解）　力の釣り合いを考えて、

　　（１/２）Ｔ_Ａ＝（/２）Ｔ_Ｂ　、（/２）Ｔ_Ａ＋（１/２）Ｔ_Ｂ＝Ｗ

　これより、　Ｔ_Ａ＝Ｔ_Ｂ　なので、　Ｔ_Ｂ＝（１/２）Ｗ　すなわち、　Ｔ_Ａ＝（/２）Ｗ

　棒の全長をＬとすると、Ｇの周りのモーメントを考えて、

　　Ｔ_Ａsin（６０°−θ）・（Ｌ/２）＝Ｔ_Ｂsin（３０°＋θ）・（Ｌ/２）

　よって、　（sin６０°cosθ−cos６０°sinθ）＝sin３０°cosθ＋cos３０°sinθ　より、

　　（−tanθ）＝１＋tanθ

　　したがって、　tanθ＝１/　から、　θ＝３０°

問題７　重さ５ｋｇｗの物体Ａと３ｋｇｗの物体Ｂとを軽い糸で結び、粗な斜面に載せてある。物
　　　　体と斜面との摩擦係数はそれぞれμ_Ａ＝０．２、μ_Ｂ＝０．３とする。斜面の傾きがしだ
　　　　いに大きくなり、物体が滑り始めるときの斜面の傾角θを求めよ。

　　　　

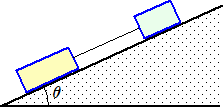
（解）　物体が滑り始めるときの糸の張力をＴ、物体Ａ、Ｂに働く面の抗力をＮ_Ａ、Ｎ_Ｂ、最大摩

　擦力をＦ_Ａ、Ｆ_Ｂとすると、　Ｔ＋Ｆ_Ａ＝５sinθ　、Ｎ_Ａ＝５cosθ　、Ｆ_Ａ＝０．２Ｎ_Ａ　より、

　　　　Ｔ＋０．２×５cosθ＝５sinθ

　同様にして、Ｔ＋３ｓｉｎθ＝０．３×３cosθ　なので、　cosθ−３sinθ＝５sinθ−０．９cosθ

　よって、　８sinθ＝１．９cosθ　より、　tanθ＝１．９/８＝０．２３８　なので、

　　θ＝１３°＋１°×（２３８−２３１）/（２４９−２３１）＝１３．４°

問題８　つるまきばねの下端に２０ｇのおもりをつるしたら６ｃｍ伸びた。このつるまきばねの
　　　　下端から全長の１/３のところに１５ｇのおもりをつるしたら何ｃｍ伸びるか？

（解）　フックの法則から、２０＝６ｋ　より、　ｋ＝１０/３（ｇｗ/ｃｍ）

　　　１５ｇのおもりを下端につるして ｘ ｃｍ伸びるとすると、　１５＝ｋｘ　より、　ｘ＝９/２（ｃｍ）

　　全体が一様に伸びるとして、求める伸びは、　（９/２）×（２/３）＝３（ｃｍ）

問題９　長さＬｃｍのつるまきばねの両端を上下Ｌｃｍだけ離れた２点に固定する。上から
　　　　 ｘ ｃｍのところにおもりを結びつける。おもりの位置の下がりを最大にするには、ｘ
　　　　の値をどうとればよいか。

（解）　おもりの重さをＷｇｗとし、ｙ ｃｍ伸びて釣り合ったものとすると、フックの法則から、

　　　おもりの上の部分では、張力 Ｔ₁＝ｋ（Ｌ/ｘ）ｙ

　　　おもりの下の部分では、押し上げの力 Ｔ₂＝ｋ（Ｌ/（Ｌ−ｘ））ｙ

　なので、釣り合うことから、　ｋ（Ｌ/ｘ）ｙ＋ｋ（Ｌ/（Ｌ−ｘ））ｙ＝Ｗ

　すなわち、　ｙ＝（Ｗ/（KＬ））/（１/ｘ＋１/（Ｌ−ｘ）） を最大にするには、ｚ＝１/ｘ＋１/（Ｌ−ｘ）

　を最小にすればよい。　ｄｚ/ｄｘ＝−１/ｘ²＋１/（Ｌ−ｘ）²＝２Ｌ（ｘ−Ｌ/２）/ｘ²（Ｌ−ｘ）²

　から、ｚは、ｘ＝Ｌ/２ で極小かつ最小となる。

　以上から求めるｘ の値は、Ｌ/２（ｃｍ）


（コメント）　微分 ｄｚ/ｄｘ を使わずとも、ｚ＝Ｌ/ｘ（Ｌ−ｘ） から、
　　　　　　ｘ（Ｌ−ｘ）＝−ｘ²＋Ｌｘ＝−（ｘ−Ｌ/２）²＋Ｌ²/４　より、　ｘ＝Ｌ/２　を見いだす方が
　　　　　高校生向けかな？

問題１０　１ｋｇｗの力で引っ張ると長さが１．５倍に伸びるゴムひもがある。これを水平に張
　　　　　　り中央におもりを吊したら、ゴムひものなす角が６０°になった。このおもりの重さ
　　　　　　はいくらか？

　　　　　　

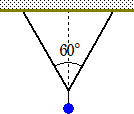
（解）　ゴムひもの長さをＬ（ｃｍ）とする。張力をＴとすると、題意より、　Ｔ＝２（ｋｇｗ）

　　また、釣り合うことから、２Ｔcos３０°＝Ｗ　より、　Ｗ＝Ｔ＝２（ｋｇｗ）

問題１１（アルキメデスの原理）

　水が入ったビーカーに、質量ｍ（ｇ）、密度ｎ（ｇ/ｃｍ³）の物体を細い糸で吊り、これが全部
隠れるまで水中に入れビーカーの壁や底につかないようにした。質量はいかほど増えるか？

（解）　最初の水が入っただけのビーカーの質量をＭ（ｇ）とする。

　　糸の張力をＴとすると、アルキメデスの原理から、　Ｔ＝ｍｇ−（ｍ/ｎ）ｇ　（ｄｙｎ）

　　物体の入ったビーカーの質量をＦとすると、釣り合いの関係から、

　　　Ｆｇ＝（Ｍ＋ｍ）ｇ−Ｔ＝Ｍｇ＋（ｍ/ｎ）ｇ　より、ｍ/ｎ（ｇ）だけ質量が増える。

問題１２　氷を食塩水に浮かべたところ、体積のちょうど１/９が水面上に出たという。氷の比
　　　　　重を０．９２７として、この食塩水の密度を求めよ。

（解）　氷の体積をＶ（ｃｍ³）、食塩水の密度をｎ（ｇ/ｃｍ³）とおくと、釣り合いの関係から、

　　　０．９２７Ｖ＝（８/９）Ｖ・ｎ　より、　ｎ＝１．０４２８７５　　よって、およそ１．０４（ｇ/ｃｍ³）

問題１３　容器内の水に浮かんでいる氷が溶けると水位は変化するか？

（解）　釣り合いの関係から、氷の重さは水面下の体積の水の重さに等しい。溶けても重さ

　　に変化がないので、水位も変化しない。

問題１４　ある点が ｘ＝２＋６ｔ−ｔ² の運動をしているとき、ｘ＝８（ｍ）を通るときの速さを求
　　　　　めよ。また、速さが０になるのはどこか？

（解）　ｖ＝ｄｘ/ｄｔ＝６−２ｔ　より、　ｔ＝３−ｖ/２　を　ｘ＝２＋６ｔ−ｔ²　に代入して、

　　　ｘ＝２＋６（３−ｖ/２）−（３−ｖ/２）²＝−ｖ²/４＋１１　から、　ｖ²＝４（１１−ｘ）

　　ｘ＝８　のとき、　ｖ²＝１２　から、　ｖ＝±２（ｍ/ｓ）

　　また、ｖ＝０　として、　ｘ＝１１（ｍ）

問題１５　１秒間に２回転する円運動の加速度を求めよ。

（解）　題意より、角速度ω＝４π　なので、　ｘ＝１０sin４πｔ

　　　よって、　ｄｘ/ｄｔ＝４π・１０cos４πｔ　、ｄ²ｘ/ｄｔ²＝−１６π²・１０sin４πｔ

問題１６（運動方程式）

　質量ｍ_１の物体の下に質量ｍ₂の物体を軽い糸で吊るし、同時に加速度αでつり上げたと
きの糸の張力を求めよ。

（解）　質量ｍ_１の物体をつり上げる張力をＴ₁、質量ｍ₂の物体が質量ｍ_１の物体を引っ張る

　　　張力をＴ₂とすると、運動の方程式から、

　　　　　ｍ_１α＝Ｔ₁−Ｔ₂−ｍ_１ｇ　、　ｍ₂α＝Ｔ₂−ｍ₂ｇ

　　　辺々加えて、　（ｍ_１＋ｍ₂）α＝Ｔ₁−（ｍ_１＋ｍ₂）ｇ　より、　Ｔ₁＝（ｍ_１＋ｍ₂）（α＋ｇ）

　　　また、　Ｔ₂＝ｍ₂（α＋ｇ）

問題１７（運動方程式）

　質量ｍ_１の物体と質量ｍ₂の物体を軽い伸びない糸で結んでなめらかな釘にかける。
ｍ_１＞ｍ₂のとき、ｍ_１の方は下降し、ｍ₂の方は上昇する。このとき、加速度αと糸の張力Ｔ
を求めよ。

（解）　運動の方程式から、

　　　　　ｍ_１α＝ｍ_１ｇ−Ｔ　、　ｍ₂α＝Ｔ−ｍ₂ｇ

　　辺々加えて、　（ｍ_１＋ｍ₂）α＝（ｍ_１−ｍ₂）ｇ　より、　α＝（ｍ_１−ｍ₂）ｇ/（ｍ_１＋ｍ₂）

　　また、　Ｔ＝ｍ_１ｇ−ｍ_１α＝２ｍ_１ｍ₂ｇ/（ｍ_１＋ｍ₂）

問題１８　鉛直線上の２定点に糸の両端を固定し、糸の中点におもりをつけて鉛直線の周
　　　　　りに回転させるｔき、次第に回転を速くしてゆくと、糸の上半部と下半部の何れが早
　　　　　く切れるか？

（解）　慣性力をＦ、上半部、下半部の糸の張力をＴ₁、Ｔ₂、糸の鉛直線とのなす角をθとす

　　　ると、水平方向の釣り合いの関係から、　Ｆ＝Ｔ₁sinθ＋Ｔ₂sinθ

　　　鉛直方向の釣り合いの関係から、　Ｔ₁cosθ＝ｍｇ＋Ｔ₂cosθ

　　　Ｔ₂を消去して、　Ｆcosθ−Ｔ₁sinθcosθ＝Ｔ₁sinθcosθ−ｍｇsinθ

　　　すなわち、　Ｔ₁＝（Ｆcosθ＋ｍｇsinθ）/（２sinθcosθ）

　　　Ｔ₁を消去して、　Ｆcosθ＝Ｔ₂sinθcosθ＋ｍｇsinθ＋Ｔ₂sinθcosθ

　　　すなわち、　Ｔ₂＝（Ｆcosθ−ｍｇsinθ）/（２sinθcosθ）

　　このとき、０＜θ＜π/２　の範囲では、　Ｔ₁＞Ｔ₂

　　　よって、上半部の方が早く切れる。

問題１９　下図のような斜面に質量Ｍｇの物体Ａと質量ｍｇ（ただし、Ｍ＞ｍ）の物体Ｂが細い
　　　　　　糸で結ばれ、さらに物体Ｂには端Ｘが固定された弦巻ばねの端Ｙが結ばれている。
　　　　　　このばねは、１ｇｗの力で引っ張るとｋｃｍ伸びる。このとき、次の問いに答えよ。

　　　


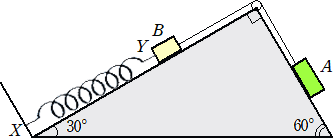
（１）　上図にあるような状態でつりあって静止しているとき、ばねの伸びはいくらか？
（２）　上図にあるような状態でつりあって静止しているとき、糸が突然切れた。このとき、物
　　体Ａと物体Ｂが斜面を滑り落ちる加速度をそれぞれ求めよ。
　　　ただし、重力加速度をｇｃｍ/ｓ²とする。

（解）（１）　ばねの伸びをｘ（ｃｍ）とすると、ばねの弾力は、　ｘ/ｋ（ｇｗ）

　　　　　よって、　Ｍｇcos３０°＝ｍｇcos６０°＋ｘ/ｋ

　　　　　　これより、　ｘ＝ｋｇ（Ｍ−ｍ）/２

（２）　物体Ａ、Ｂの加速度をそれぞれ ａ、ａ’とおくと、

　　　　　Ｍａ＝Ｍｇcos３０°より、　ａ＝ｇ/２

　　　　　ｍａ’＝ｍｇcos６０°＋ｘ/ｋ＝ｍｇ/２＋ｇ（Ｍ−ｍ）/２　より、ａ’＝Ｍｇ/（２ｍ）

問題２０（力学的エネルギー保存の法則）

　質量ｍの物体を鉛直上方に投げ出したとき、速さと高さの間にはどんな関係があるか。

（解）　物体の初速度をＶ₀、高さｈにおける物体の速度をＶとおくと、

　　　　　（１/２）ｍＶ₀²＝（１/２）ｍＶ²＋ｍｇｈ　より、　Ｖ₀²−Ｖ²＝２ｇｈ

問題２１（力学的エネルギー保存の法則）

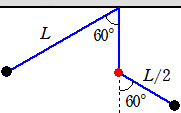
　質量ｍのおもりを長さがＬの糸で天井から吊るし、糸を鉛直線と６０°傾けておく。おもりを
放して糸が鉛直になったとき、糸の中点がそこにある釘によって止められたので以後は長さ
がＬ/２の振り子と変わった。この振り子が鉛直線と６０°傾いたとき、おもりの速さＶはどれ
だけになるか。

　　　　

（解）　天井よりＬだけ下の点を高さの基準に選ぶと、

　　　０＋ｍｇＬ（１−cos６０°）＝（１/２）ｍＶ²＋ｍｇ（Ｌ/２）（１−cos６０°）

　　よって、　Ｖ²＝ｇＬ/２　より、　Ｖ＝√（ｇＬ/２）

問題２２（比熱）

　５０℃のアルコール（比熱０．５５）３０ｇと６０℃の水７０ｇをビーカー（質量２０ｇ、比熱０．１２
温度２５℃）の中に入れたら、全体は何度になるか。

（解）　アルコール３０ｇは水に換算すると、３０×０．５５＝１６．５ｇに相当する。ビーカー２０ｇ

　は水に換算すると、２０×０．１２＝２．４ｇに相当する。

　混ぜ合わせてＴ℃になるとして、水の得た熱量の総和は０であるので、

　　７０（Ｔ−６０）＋１６．５（Ｔ−５０）＋２．４（Ｔ−２５）＝０

　よって、　８８．９Ｔ＝４２００＋８２５＋６０＝５０８５　より、　Ｔ＝５７．１９９１

　すなわち、全体は、５７．２℃になる。

問題２３　６０℃の水８ｋｇに０℃の氷を２ｋｇ入れたところで、３２℃になった。氷の融解熱を
　　　　　　求めよ。

（解）　氷の融解熱をｍ（cal/ｇ）とおくと、２０００ｍ＋２０００×３２＝８０００（６０−３２）

　　　よって、　２０００ｍ＝２２４０００−６４０００＝１６００００　より、　ｍ＝８０

問題２４　次の現象を説明せよ。

（１）　虹に色が見える
（２）　水面上の油の油膜に色が見える
（３）　朝日、夕日が赤く見え、晴天の空が青く見える
（４）　白色光の下で赤色ガラス板を通して見ると、白色の物体でも赤く見える

（解）（１）　分散　（２）　干渉　（３）　散乱　（４）　ガラスの吸収

問題２５（クーロンの法則）

　長さＬ（ｃｍ）、質量ｍ（ｇ）の２つのコルク振り子を同じ地点から吊り、コルクに等量の電荷ｑ
を与えたところ、互いに反発して、糸の間の角が２αだけ開いて静止した。電荷はいかほど
か。

（解）　反発力をＦとして、釣り合いから、　Ｆ＝ｍｇtanα

　　　クーロンの法則から、　Ｆ＝ｑ²/（２Ｌsinα）²

　　よって、　ｑ²/（２Ｌsinα）²＝ｍｇtanα　から、　ｑ＝２Ｌsinα√（ｍｇtanα）

問題２６　１００Ｖの電源で１Ａの電流が流れるタングステン電球のタングステン線の抵抗は、
　　　　　　２０℃ではいくらか。電灯が点火しているときのタングステンの温度を２７００℃とし、
　　　　　　タングステンの抵抗の温度係数を５３×１０^-4として計算せよ。

（解）　２７００℃における抵抗は、１００Ωなので、求める抵抗をＲとすると、

　　　　１００＝Ｒ（１＋５３×１０^-4×（２７００−２０））＝１５．２Ｒ　より、　Ｒ＝６．６（Ω）

問題２７　３つの抵抗線を図のように連結したとき、ＡＢ間の抵抗はどれほどか。また、Ａ、Ｂ
　　　　　の電位をそれぞれＶ_Ａ、Ｖ_Ｂとすれば、Ｃの電位Ｖ_Ｃはいくらか。

　　　　

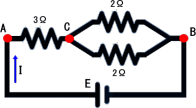
（解）　ＢＣ間の抵抗をＲとすると、　１/Ｒ＝１/２＋１/２＝１　より、　Ｒ＝１

　　　よって、ＡＢ間の抵抗は、　３＋１＝４（Ω）

　　このとき流れている電流 Ｉ は、　Ｉ ×４＝Ｖ_Ａ−Ｖ_Ｂ

　　よって、　Ｖ_Ａ−Ｖ_Ｃ＝　Ｉ ×３＝（Ｖ_Ａ−Ｖ_Ｂ）×（３/４）　より、

　　　Ｖ_Ｃ＝Ｖ_Ａ−（Ｖ_Ａ−Ｖ_Ｂ）×（３/４）＝（Ｖ_Ａ＋３Ｖ_Ｂ）/４


（コメント）　当然ながら、これは内分の公式からも求められますね。

問題２８　下図の回路で、Ｅは起電力１．５Ｖ、内部抵抗３Ωの電池、Ｒは７Ωの抵抗線、Ｃ
　　　　　はともに容量２μＦのコンデンサーである。ＡＢ間、およびＡＰ間の電圧を求めよ。

　　　

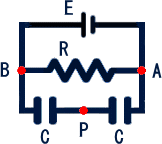
（解）　ＡＢ間を流れる電流 Ｉ は、　Ｉ＝１．５/（３＋７）＝０．１５（Ａ）

　　よって、　ＡＢ間の電圧は、　０．１５×７＝１．０５（Ｖ）

　また、コンデンサーの容量が等しいので、ＡＰ間の電圧は、　１．０５÷２＝０．５３（Ｖ）

問題２９（キルヒホッフの法則）

　下図の回路で、Ｅ₁＝４Ｖ、Ｒ₁＝８Ω、Ｅ₂＝２Ｖとして、Ｒ₂をいくらにすればＡＢを流れる電
流が０となるか。

　　

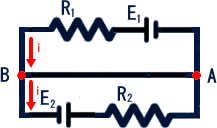
（解）　上図で、電流 ｉ は、Ｅ₁Ｒ₁ＢＥ₂Ｒ₂ＡＥ₁を一巡する。

　回路Ｅ₁Ｒ₁ＢＡＥ₁について、ＡＢを流れる電流は０なので、　ｉ・Ｒ₁＝Ｅ₁

　回路Ｅ₂Ｒ₂ＡＢＡＥ₂について、ＡＢを流れる電流は０なので、　ｉ・Ｒ₂＝Ｅ₂

　よって、　Ｒ₂＝Ｒ₁・Ｅ₂/Ｅ₁＝８・（２/４）＝４（Ω）



　　以下、工事中！