岆嵎偵偮偄偰 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂偁傞堦偮偺栤戣傪夝偙偆偲偡傞偲偒丄偁傞摿暿側応崌傪彍偄偰丄岆嵎偼昁偢婲偙傝摼傞丅
側偤側傜丄悢抣寁嶼偱偼丄昅嶼偵偟傠揹戩傪巊偆偵偟傠丄柍尷偺寘悢傪帩偮悢抣偼埖偊側偄
偐傜偱偁傞丅
丂悢妛偱偼丄棟榑抣偱悢抣寁嶼偡傞偺偱丄暯曽崻傗懳悢側偳偺偄傠偄傠側婰崋傪嬱巊偟偰丄
偒偭偪傝寁嶼寢壥傪帵偡偙偲偑壜擻偱偁傞偑丄懠偺幚尡壢妛乮暔棟丄壔妛丄惗暔丄丒丒丒乯偱偼丄
幚尡抣偱僨乕僞傪張棟偡傞偺偱丄岆嵎偲偺摨嫃偼廻柦偱偁傞丅
丂 偳傫側偵惓偟偄寁嶼傪偡傞恖偱傕丄偳傫側偵桪廏側僐儞僺儏乕僞偱傕丄偙偺偙偲偼旔偗傞偙
偲偺偱偒側偄偙偲偱偁傞丅
| 椺丂悢妛偱偼丄捠忢丄暘悢昞婰丂偨偲偊偽丄 |
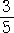 |
丂傪梡偄傞偑丄幚尡抣偲偟偰偼丄彫悢昞婰 |
| 丂丂0.6丂傪梡偄傞偺偑忢幆偲側偭偰偄傞丅0.60丄0.600丄0.6000丄丒丒丒丂側偳偵傛偭偰丄偦偺悢 |
| 丂丂偺桳岠寘悢傪帵偟丄偦偺悢抣偺惛搙傪昞偡偙偲偵側偭偰偄傞丅 |
丂嬶懱揑側栤戣傪丄悢妛偺栤戣偲偟偰婰弎偡傞偲偒丄晄惓妋側僨乕僞傗壖掕偑擖傞応崌偑
偁傞丅
丂偙偺偲偒丄偄偔傜惓妋偵寁嶼傪峴偭偰傕丄寁嶼寢壥偼堄枴偺側偄傕偺偵側偭偰偟傑偆丅
丂栤戣偺婰弎偺抜奒偱惗偢傞岆嵎傪丄擖椡岆嵎乮娤應岆嵎乯偲偄偆丅
丂悢妛揑偵栤戣傪夝愅偡傞偲偒丄忦審偺娙慺壔傪峴偆偙偲偑懡偄丅杸嶤椡傗嬻婥掞峈傪柍
帇偟偨傝丄媴柺側偺偵暯柺偲峫偊偨傝丄柍尷夞偺憖嶌偑昁梫側偺偵桳尷夞偱懪偪愗偭偨傝
偡傞丅
丂岆嵎傪堄幆偡傞応崌丄偙傟傜偺娙慺壔偼拲堄怺偔傗傜側偗傟偽側傜側偄丅
丂栤戣傪夝愅偟丄悢抣寁嶼偺栤戣傊捈偡偲偒偵惗偢傞岆嵎傪丄夝愅岆嵎偲偄偆丅
丂僾儘僌儔儉傪慻傫偱僐儞僺儏乕僞偱寁嶼傪峴偆抜奒偵側偭偰傕岆嵎偼婲偙傝摼傞丅
丂寘悢偺挿偄悢傪寛傔傜傟偨寘悢偺悢偱嬤帡偡傞憖嶌傪丄乽娵傔乿偲偄偆丅寁嶼偵偼丄偦偺
偨傔偵惗偢傞岆嵎丄娵傔岆嵎偑偮偒傕偺偱偁傝丄寛掕揑側抜奒偱偺娵傔岆嵎偑丄寢壥偵
戝偒偔塭嬁偡傞応崌偑偁傞丅
丂偙偺傛偆偵旕忢偵懡偔偺岆嵎偑懚嵼偟丄寁嶼寢壥偵媦傏偡塭嬁偼寁傝抦傟側偄丅偦偺庺
敍偐傜摝傟傞偙偲偼丄偲偰傕擄偟偔偐偮崲擄偱偁傞丅
丂偦偙偱丄岆嵎偺塭嬁傪嵟彫尷偵梷偊傞傛偆偵丄栤戣偵懳張偡傞偙偲偑廳梫偵側偭偰偔傞丅
丂岆嵎偼丄丂乮應掕抣乯亅乮恀偺抣乯丂偱媮傔傜傟傞丅
丂扐偟丄恀偺抣偼丄愨懳偵抦傞偙偲偑晄壜擻側抣側偺偱丄屄乆偺應掕抣偵懳偡傞岆嵎傕愨
懳偵抦傞偙偲偑偱偒側偄抣偱偁傞丅
丂廬偭偰丄扨偵岆嵎偲偄偆応崌偼丄嵟戝岆嵎傪巜偡応崌偑懡偄丅
丂栤戣傪夝偔抜奒偱梌偊傜傟偨悢抣偑丄惓妋側抣側偺偐丄岆嵎傪娷傓抣側偺偐敾抐偵柪偆
応崌偑偁傞丅偦偺応崌偼丄桳岠悢帤偵拲堄偟偰寁嶼偡傞偙偲偵側傞丅
<<寢壥偺桳岠悢帤偺寛傔曽>>
乮侾乯摎偺桳岠悢帤偺寘悢偑巜掕偝傟偰偄傞偲偒
丂侾寘懡偔嶼弌偟丄巐幪屲擖偵傛偭偰丄強梫偺寘悢偲偡傞
乮俀乯摎偺桳岠悢帤偺寘悢偑巜掕偝傟偰偄側偄偲偒
丂乮僀乯栤戣拞偺桳岠悢帤偺寘悢偑偦傠偭偰偄傞偲偒
丂丂栤戣拞偺桳岠悢帤偺寘悢偵偁傢偣傞
丂乮儘乯栤戣拞偺桳岠悢帤偺寘悢偑偦傠偭偰偄側偄偲偒
丂丂嵟傕彫偝偄桳岠悢帤偺寘悢偵偁傢偣傞
丂乮椺丂俁俉丏俈係亐俇丏俋亖俆丏俇侾係係俋丂仺俆丏俇乯
丂乮僴乯栤戣拞偺桳岠悢帤偺寘悢偑柧帵偝傟偰偄側偄偲偒
丂丂婯懃丗栤戣拞偺悢偺寘悢偲傎傏摍偟偔偲傞
丂丂丂乮椺丗俁丏俀俈亊俀丏俆俋亖俉丏係俇俋俁丂仺俉丏係俈乯
丂丂婯懃丗値忔偍傛傃値忔崻偼丄尦偺悢偺寘悢偲傎傏摍偟偔偲傞
丂丂丂乮椺丗侽丏俉俈俇偺俁忔亖侽丏俇俈俀俀俀丒丒丒丂仺侽丏俇俈俀
丂丂丂丂丂俁忔崻侽丏俉俈俇亖侽丏俋俆俇俉俀丒丒丒丂仺侽丏俋俆俈乯
丂丂婯懃丗偄傠偄傠側寘悢偺悢偑崿嵼偟偰偄傞偲偒偼丄拞娫偺寘悢傪偲傞
丂丂丂乮椺丗係丏俈俀俇亊俆丏俉亖俀俈丏係侾侽俉丒丒丒丂仺俀俈丏係乮係寘丄俀寘仺俁寘乯
丂丂丂丂丂俆丏係俁亊俀丏俆俉俀亖俀丏侾侽俁侽俀丒丒丒丂仺俀丏侾侽乮俁寘丄係寘仺俁寘乯乯
<<搑拞寁嶼偺桳岠悢帤偺寛傔曽>>
丂栤戣拞偺悢偺寘悢丄摎偵梫媮偝傟偰偄傞寘悢傛傝侾寘掱搙懡偔偲傞
丂丂丂乮椺丗丂俆丏俁俉亊俇丏俈係亊係丏侾俀亊係丏俁俈
丂丂丂丂丂丂丂俁俇丏俀俇侾俀
丂丂丂丂亖俁俇丏俀俇亊係丏侾俀亊係丏俁俈
丂丂丂丂丂侾係俋丏俁俋侾俀
丂丂丂丂亖侾係俋丏係亊係丏俁俈
丂丂丂丂亖俇俆俀丏俉俈俉亖俇俆俁
丂丂偦偺傑傑寁嶼偡傞偲丄俇俆俀丏俉俇侾侾俁侾俉偱丄傗偼傝俇俆俁乯
<<壛嶼丒尭嶼偺寢壥偺桳岠悢帤偺寛傔曽>>
丂嵟傕嵟戝岆嵎偺戝偒偄悢偲枛埵傪堦抳偝偣傞
丂丂丂乮椺丗丂俈俁俇丏俁俈亄俋侾丏係俇俉亄侾俀俇俆丏俆亄俉丏俈俁俇俁亖俀侾侽俀丏侽俈係俁丂仺俀侾侽俀丏侾乯
丂奺悢傪強梫偺寘傛傝侾埵掅偔偲傝寁嶼偟偰傕傛偄
丂丂丂乮椺丗丂俈俁俇丏俁俈亄俋侾丏係俇俉亄侾俀俇俆丏俆亄俉丏俈俁俇俁
丂丂丂丂丂亖俈俁俇丏俁俈亄俋侾丏係俈亄侾俀俇俆丏俆亄俉丏俈係亖俀侾侽俀丏侽俉丂仺俀侾侽俀丏侾乯
<<晜摦彫悢揰昞帵偝傟偨悢偺巐懃墘嶼>>
丂丂俶亖亇倎亊侾侽n丂丂乮倎丗壖悢晹偱丄侽亝倎亝侾丄値丗巜悢晹乯
偺宍偺悢抣寁嶼偼丄師偺傛偆側庤弴偱峴偆丅
乮侾乯丂忔彍嶼偺応崌
丂乮鶣乯丂晞崋傪寛傔傞
丂乮鶤乯丂壖悢晹偺忔彍嶼傪峴偆乮俀攞偺寘悢傑偱寁嶼偡傞乯
丂乮鶥乯丂巜悢晹偺壛尭嶼傪峴偆
丂乮鶦乯丂惓婯壔乮彫悢戞堦埵偺悢傪侽埲奜偺悢偵偡傞偙偲乯偲娵傔傪峴偆
椺丂乮侽丏侾俁俆俈亊侾侽3乯亊乮侽丏俀係俇俉亊侾侽2乯
丂亖乮侽丏侾俁俆俈亊侽丏俀係俇俉乯亊侾侽5
丂亖侽丏侽俁俁係俋侽俈俇亊侾侽5
丂亖侽丏俁俁係俋亊侾侽4
乮俀乯丂壛尭嶼偺応崌
丂乮鶣乯丂巜悢晹傪戝偒偄曽偵崌傢偣傞
丂乮鶤乯丂壖悢晹偺壛尭嶼傪峴偆乮寘悢傪悢寘懡偔寁嶼偡傞乯
丂乮鶥乯丂惓婯壔乮彫悢戞堦埵偺悢傪侽埲奜偺悢偵偡傞偙偲乯偲娵傔傪峴偆
椺丂乮侽丏侾俁俆俈亊侾侽3乯亄乮侽丏俀係俇俉亊侾侽2乯
丂亖乮侽丏侾俁俆俈亊侾侽3乯亄乮侽丏侽俀係俇俉亊侾侽3乯
丂亖乮侽丏侾俁俆俈亄侽丏侽俀係俇俉乯亊侾侽3
丂亖侽丏侾俇侽俁俉亊侾侽3
丂亖侽丏侾俇侽係亊侾侽3
丂壛尭嶼偵偍偄偰丄拲堄偟側偗傟偽側傜側偄応崌偑偁傞丅
丂傎傏摍偟偄悢偺尭嶼偺応崌偵偼丄桳岠悢帤偺憆幐乮偙傟傪丄寘棊偪偲偄偆乯偲偄偆尰徾偑
婲偒傞丅偙偺応崌偼丄強梫偺寘悢傛傝俁乣係寘懡偔偲偭偰寁嶼偡傞丅
椺丂乮侽丏侾俁俆俈亊侾侽3乯亅乮侽丏侾俁俆俆亊侾侽3乯亖侽丏侽侽侽俀亊侾侽3亖侽丏俀
丂忋婰偺寁嶼偱偼丄桳岠悢帤係寘偺悢偑桳岠悢帤侾寘偺悢偵寘棊偪偟偰偄傞丅偙傟傪丄俁寘
偺寘棊偪偲偄偆丅
丂堦斒偵丄倫寘偺寘棊偪偑偁傞偲丄偦偺憡懳岆嵎偼丄侾侽p 攞偵傕側傞偲偄偆丅
丂摨條偺偙偲偑暯曽崻偺寁嶼偱傕婲偙傝摼傞丅
丂椺偊偽丄廫暘彫偝偄倃偵懳偟偰丄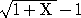 偺抣傪媮傔傞応崌偱偁傞丅
偺抣傪媮傔傞応崌偱偁傞丅
丂丂倃亖侽丏侾俁俆俈亊侾侽-2 偵懳偟偰丄侾亄倃亖侾丏侽侽侾係丂傛傝丄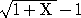 亖侽丏俈亊侾侽-3 埵
亖侽丏俈亊侾侽-3 埵
偲寁嶼偱媮傔傜傟傞偑丄寘棊偪偵傛傝丄懡偔偺岆嵎傪娷傫偱偟傑偭偰偄傞丅
丂寘棊偪傪杊偖曽朄偲偟偰偼丄暘巕偺桳棟壔偲偄偆曽朄偑傛偔抦傜傟偰偄傞丅
幚嵺偵丄
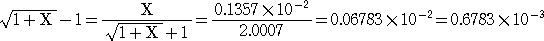
丂偳偪傜偑傛傝恀偺抣偵嬤偄偐偲偄偆偲丄
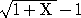 佮 侽丏侽侽侽俇俈俉俁亖侽丏俇俈俉俁亊侾侽-3 丂偲偄偆偙偲偐傜柧傜偐偱偁傠偆丅
佮 侽丏侽侽侽俇俈俉俁亖侽丏俇俈俉俁亊侾侽-3 丂偲偄偆偙偲偐傜柧傜偐偱偁傠偆丅
丂俀師曽掱幃偺夝傪丄夝偺岞幃傪梡偄偰悢抣寁嶼偡傞応崌丄忋偲摨條側偙偲偑婲偙傝摼傞丅
乮倎倃2亄倐倃亄們亖侽丂偵偍偄偰丄係們 偵斾傋偰丄倐2 偑廫暘戝偒偄応崌乯
偦偺応崌偼柪傢偢暘巕偺桳棟壔傪幚峴偟偰丄寘棊偪偵傛傞憡懳岆嵎偺憹壛傪杊偘偽傛偄丅
丂傑偨丄師偺傛偆偵丄栤戣偺弌戣幰偑拲堄偟側偗傟偽側傜側偄応崌傕偁傞丅
椺丂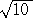 亖俁丏侾俇丂偺偲偒丄
亖俁丏侾俇丂偺偲偒丄
丂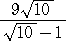
偺抣傪媮傔傛丅
丂捠忢偼丄暘曣傪桳棟壔偟偰丄
丂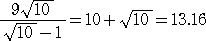
偲寁嶼偟偰偔傟傞傕偺偲弌戣幰偼婜懸偡傞偑丄師偺傛偆偵寁嶼偡傞恖傕偄側偄傢偗偱偼側偄丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂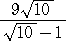 |
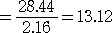 |
丂巹偩偭偨傜丄偙偺夝摎傕惓夝偲偡傞偑丄堦斒揑偵偼丄偳偆側傫偩傠偆偐丠
<<妡偗嶼偺夞悢>>
丂丂悢抣寁嶼傪偡傞偲偒丄偱偒傞偩偗妡偗嶼偺夞悢偼尭傜偟偨曽偑傛偄丅
丂俙10 傪寁嶼偡傞偲偒丄俙丆俙2丆俙3丆丒丒丒偲弴師寁嶼偟偰偄偔偺偼丄寴幚偱偁傞偑丄旕擻棪偱
偁傞丅幚偼丄俙10 偼丄係夞偺妡偗嶼偱媮傔傞偙偲偑弌棃傞丅
丂乮乮俙2乯2亊俙乯2
偲暘夝偡傟偽傛偄丅
丂摨條偵偟偰丄俙100000丂偺妡偗嶼偺夞悢偼丄俀侽夞偱嵪傓偟丄俙488丂偼丄侾侾夞偺妡偗嶼偱
嵪傓丅壗屘偐偼丄奆偝傫偺壽戣偲偟偨偄丅
乮嶲峫暥專丗D.G.Moursund C.S.Duris
丂丂丂丂丂丂Elementary Theory and Application of Numerical Analysis乮McGraw-Hill)
丂丂丂丂栰嶈徍峀丂悢抣夝愅偵偮偄偰乮徍榓俆俈擭搙恄撧愳導悢妛島嵗乯
丂丂丂丂椡晲忢師丒杒懞椙晇丒惔悈岝帯丂暔棟嘥丒嘦乮悢尋弌斉乯
丂丂丂丂柤庢丂椇丂挊丂慄宍寁嶼乮挬憅彂揦乯乯
