重ね合わせの理　 　　　　　　　　　　　　　　　　　　　　　　　　　　　

　重ね合わせの理は、キルヒホッフの法則などを用いて電気回路を計算するときに利用さ
れる手法のひとつである。この重ね合わせの理は連立一次方程式の解法にも応用される。

　この事実に興味・関心があり、このページを起こすこととした。

　連立一次方程式の解法は原理的には難しくないが、係数が分数（小数）などの場合、数
値計算は非常に大変である。手計算で行う場合、未知数の数が ｎ 倍になると、それを解く
手間は ｎ³ 倍にもなるという。

　重ね合わせの理を理解するために、次の例から考えてみよう。

例　次の連立方程式を解け。　　３ｘ＋４ｙ＝６　、２ｘ−３ｙ＝４

　この問題は中学２年生レベルである。中学生だったら次のように解くのだろう。

（解）　（第１式）×３＋（第２式）×４　より、　１７ｘ＝３４　　よって、ｘ＝２　、ｙ＝０　（終）

　これに対して、「重ね合わせの理」を用いた解法は次のようになる。

（解）　２組の連立方程式を考える。

　　（１）　３ｘ＋４ｙ＝１　、２ｘ−３ｙ＝０

　　（２）　３ｘ＋４ｙ＝０　、２ｘ−３ｙ＝１

　（１）において、　ｘ＝３ｍ　、ｙ＝２ｍ　なので、　１７ｍ＝１　より、　ｍ＝１/１７

　　　　よって、　ｘ＝３/１７　、ｙ＝２/１７

　（２）において、　ｘ＝４ｎ　、ｙ＝−３ｎ　なので、　１７ｎ＝１　より、　ｎ＝１/１７

　　　　よって、　ｘ＝４/１７　、ｙ＝−３/１７

　このとき、重ね合わせの理により、もとの連立方程式の解は、

　　ｘ＝６（３/１７）＋４（４/１７）＝３４/１７＝２　、ｙ＝６（２/１７）＋４（−３/１７）＝０　（終）

　この重ね合わせの理の正当性は次の式変形から理解される。

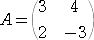とおくと、

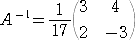なので、連立方程式は、

　　　　

と書ける。よって、

　　　　　

　重ね合わせの理は、（６，４）そのものを考えるのではなく、どちらか一方を ０ として（１，０）
や（０，１）を考える点に特徴がある。

　複数の電源がある回路で、「どちらか一方を０」とする考え方は、電源を１つずつ考えるこ
とに相当し、それらの結果を足し合わせて電流や電圧が求める方法が「重ね合わせの理」
（ｐｒｉｎｃｉｐｌｅ　ｏｆ　ｓｕｐｅｒｐｏｓｉｔｉｏｎ）である。

例　次の回路に流れる電流を求めよ。ただし、Ｖ₁、Ｖ₂、Ｖ₃ は各電池の起電力とする。

（解）
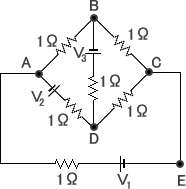　　　　左図において、ＡからＢへ流れる電流を ｘ 、ＡからＤへ
　　　流れる電流を ｙ 、ＢからＤへ流れる電流を ｚ とおくと、

　　　キルヒホッフの第一法則により、

　　　　　ＢからＣへ流れる電流は ｘ−ｚ 、
　　　　　ＤからＣへ流れる電流は ｙ＋ｚ 、
　　　　　ＣからＥを通ってＡへ流れる電流は ｘ＋ｙ

　　　となる。


　このとき、キルヒホッフの第二法則により、

回路ＡＢＣＥＡについて、　（ｘ＋ｙ）＋ｘ＋（ｘ−ｚ）＝Ｖ₁　すなわち、　３ｘ＋ｙ−ｚ＝Ｖ₁

回路ＡＤＣＢＡについて、　ｙ＋（ｙ＋ｚ）＋（−ｙ）＋（−ｘ）＝Ｖ₂　すなわち、　−ｘ＋ｙ＋ｚ＝Ｖ₂

回路ＢＤＣＢについて、　ｚ＋（ｙ＋ｚ）＋（−ｘ＋ｚ）＝Ｖ₂　すなわち、　−ｘ＋ｙ＋３ｚ＝Ｖ₃

　（第１式）＋（第２式）　より、　２ｘ＋２ｙ＝Ｖ₁＋Ｖ₂　すなわち、　ｘ＋ｙ＝Ｖ₁/２＋Ｖ₂/２

　（第２式）×（−３）＋（第２式）　より、　２ｘ−２ｙ＝−３Ｖ₂＋Ｖ₃

　　　　　　　　　　　　　　　　　　　すなわち、　ｘ−ｙ＝−３Ｖ₂/２＋Ｖ₃/２

　したがって、

　　ｘ＝Ｖ₁/４−Ｖ₂/２＋Ｖ₃/４　、ｙ＝Ｖ₁/４＋Ｖ₂−Ｖ₃/４　、ｚ＝−Ｖ₂/２＋Ｖ₃/２　　　（終）

　この問題を、重ね合わせの理を用いて解いてみよう。

（別解）　Ｖ₂＝Ｖ₃＝０　のとき、　３ｘ＋ｙ−ｚ＝Ｖ₁　、−ｘ＋ｙ＋ｚ＝０　、−ｘ＋ｙ＋３ｚ＝０

　　　　　　　　ｚ＝０　で、　３ｘ＋ｙ＝Ｖ₁　、−ｘ＋ｙ＝０　より、　ｘ＝Ｖ₁/４　、ｙ＝Ｖ₁/４

　　Ｖ₁＝Ｖ₃＝０　のとき、　３ｘ＋ｙ−ｚ＝０　、−ｘ＋ｙ＋ｚ＝Ｖ₂　、−ｘ＋ｙ＋３ｚ＝０

　　　　　　　　ｘ＝ｚ　で、　ｙ＝Ｖ₂　、ｘ＝−Ｖ₂/２　、ｚ＝−Ｖ₂/２

　　Ｖ₁＝Ｖ₂＝０　のとき、　３ｘ＋ｙ−ｚ＝０　、−ｘ＋ｙ＋ｚ＝０　、−ｘ＋ｙ＋３ｚ＝Ｖ₃

　　　　　　　　ｘ＝−ｙ　、　ｚ＝−２ｙ　で、　ｙ＝−Ｖ₃/４　、ｘ＝Ｖ₃/４　、ｚ＝Ｖ₃/２

　このとき、重ね合わせの理により、求める ｘ、ｙ、ｚ の値は、

　　　ｘ＝（Ｖ₁/４）＋（−Ｖ₂/２）＋（Ｖ₃/４）＝Ｖ₁/４−Ｖ₂/２＋Ｖ₃/４

　　　ｙ＝（Ｖ₁/４）＋（Ｖ₂）＋（−Ｖ₃/４）＝Ｖ₁/４＋Ｖ₂−Ｖ₃/４

　　　ｚ＝（０）＋（−Ｖ₂/２）＋（Ｖ₃/２）＝−Ｖ₂/２＋Ｖ₃/２　　　（終）