１次方程式や２次方程式、・・・ のように、多項式＝０ の形に対して、未知数 ｘ が指数
部分にある方程式が、所謂、指数方程式と呼ばれるものである。
例 ２^ｘ＝４ 、８^ｘ＝４ 、２^ｘ＝３ 、４^ｘ−３・２^ｘ＋２＝０ 、・・・
指数方程式を解くには、いくつかの技がある。
（１） 底を揃える
例 ２^ｘ＝４ を解け。
（解） ２^ｘ＝２^２ より、 ｘ＝２ （終）
例 ８^ｘ＝４ を解け。
（解） ２^（３ｘ）＝２^２ より、 ３ｘ＝２ よって、 ｘ＝２/３ （終）
（２） 対数の利用
例 ２^ｘ＝３ を解け。
（解） ｘ＝ｌｏｇ2３ （終）
例 ３^ｘ＝２^（ｘ＋１） を解け。
（解） ｘｌｏｇ2３＝ｘ＋１ より、 ｘ＝１/（ｌｏｇ2３−１） （終）
（３） 置き換えの利用
例 ４^ｘ−３・２^ｘ＋２＝０ を解け。
（解） ２^ｘ＝Ｘ とおくと、 Ｘ^2−３Ｘ＋２＝０ から、 （Ｘ−１）（Ｘ−２）＝０
よって、 Ｘ＝２^ｘ＝１ から、 ｘ＝０
Ｘ＝２^ｘ＝２ から、 ｘ＝１ （終）
読者のために、練習問題を残しておこう。
練習問題 ９^ｘ＋３・４^ｘ＝４・６^ｘ を解け。
（解） ３^ｘ＝Ｘ 、２^ｘ＝Ｙ とおくと、 Ｘ^２＋３Ｙ^２＝４ＸＹ
両辺をＹ^２で割ると、 （Ｘ/Ｙ）^２＋３＝４（Ｘ/Ｙ） すなわち、（Ｘ/Ｙ）^２−４（Ｘ/Ｙ）＋３＝０
よって、 Ｘ/Ｙ＝１、３ より、 （３/２）^ｘ＝１、３ を解いて、 ｘ＝０、ｌｏｇ3/2３ （終）
少しレベルアップして、指数方程式の解法に習熟しよう。
問題 方程式 ８^ｘ＋ａ・４^ｘ＋ｂ・２^ｘ＝ａ＋ｂ＋１ （ａ、ｂは定数） が０または正の異なる３
つの実数解を持つとき、ｂの取り得る値の範囲を求めよ。
（解） ２^ｘ＝Ｘ とおくと、 Ｘ^３＋ａＸ^２＋ｂＸ−ａ−ｂ−１＝０
このとき、 （Ｘ−１）（Ｘ^２＋（ａ＋１）Ｘ＋ａ＋ｂ＋１）＝０ より、
Ｘ＝１ 、Ｘ^２＋（ａ＋１）Ｘ＋ａ＋ｂ＋１＝０
ここで、 Ｘ＝２^ｘ＝１ から、 ｘ＝０ を解に持つ。
また、題意より、 Ｆ（Ｘ）＝Ｘ^２＋（ａ＋１）Ｘ＋ａ＋ｂ＋１＝０ は、１より大きい異なる２実数
解を持つので、
判別式 Ｄ＝（ａ＋１）^２−４（ａ＋ｂ＋１）＞０ より、 ａ^２−２ａ−４ｂ−３＞０
Ｆ（１）＝２ａ＋ｂ＋３＞０
−（ａ＋１）/２＞１ より、 ａ＜−３
以上から、 ｂ＜（１/４）（ａ−１）^２−１ 、ｂ＞−２ａ−３ 、ａ＜−３ を図示すると、
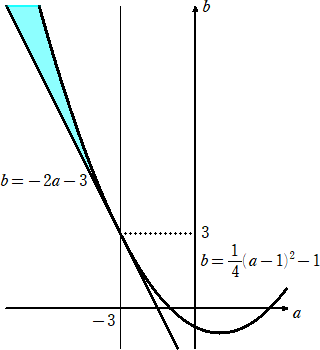
従って、ｂの取り得る値の範囲は、 ｂ＞３ （終）
（コメント） 上記問題のように、見かけは指数方程式だが、適当な置き換えにより、普通の
方程式の問題に帰着されることが多い。
（追記） 令和６年７月２７日付け
次の東北大学 文系（１９７５）の問題も練習問題になるだろう。
問題 次の連立方程式を解け。
ｘｙ＝ｙｘ 、ｌｏｇｘｙ＋ｌｏｇｙｘ＝１３/６
（解） ｘｙ＝ｙｘ の両辺の底を ｘ とする対数をとって、 ｙ＝ｘ・ｌｏｇｘｙ
ｌｏｇｙｘ＝１/ｌｏｇｘｙ なので、 ｌｏｇｘｙ＋１/ｌｏｇｘｙ＝１３/６ より、
（ｌｏｇｘｙ）2−（１３/６）ｌｏｇｘｙ＋１＝０ すなわち、 ６（ｌｏｇｘｙ）2−１３ｌｏｇｘｙ＋６＝０ から、
（２ｌｏｇｘｙ−３）（３ｌｏｇｘｙ−２）＝０ よって、 ｌｏｇｘｙ＝３/２ 、２/３
ｌｏｇｘｙ＝３/２ のとき、 ｙ＝（３/２）ｘ で、 ｘ＾（３/２）＝（３/２）ｘ
ｘ≠０ なので、 ｘ＾（１/２）＝３/２ より、 ｘ＝９/４ このとき、ｙ＝２７/８
ｌｏｇｘｙ＝２/３ のとき、 ｙ＝（２/３）ｘ で、 ｘ＾（２/３）＝（２/３）ｘ
ｘ≠０ なので、 ｘ＾（−１/３）＝２/３ より、 ｘ＝２７/８ このとき、ｙ＝９/４ （終）
ＧＡＩ さんから問題をいただきました。（令和６年７月２９日付け）
ある等式を満たす指数を探す問題です。
１x＋２x＝３x を満たす x は？ → x＝１
３x＋４x＝５x を満たす x は？ → x＝２
は見つかる。では、それぞれ次の式を満たす x は何？
（１） ２x＋３x＝４x
（２） ４x＋５x＝６x
（３） ４x＋６x＝９x
（４） ９x＋１２x＝１６x
（コメント） 手計算で求めることは無理ですね！
らすかるさんからのコメントです。（令和６年７月２９日付け）
普通に数値計算すればよいだけなら、a^x＋b^x＝c^x の解は適当な初期値から
x ← x-(a^x+b^x-c^x)/{(loga)a^x+(logb)b^x-(logc)c^x}
という漸化式で求めればよく、近似値(小数第61位を四捨五入)は、
(1) 1．507126591638653133986883360838631164373994094485656896675364
(2) 2．487939173118174667543358494964101710715178304214349713989600
(3) 1．186814390280981717544988040147644615298932643889332006235330
(4) 1．672720934462332544585431252419794866784109546317415204907841
ＧＡＩ さんからのコメントです。（令和６年７月３０日付け）
（３）（４）には明示的表示が可能となると思うんですが、（１）（２）では無理ですかね？
らすかるさんからのコメントです。（令和６年７月３０日付け）
あ、（３）（４）は解けるんですね。
(a^2)^x＋(ab)^x＝(b^2)^x から、1＋(b/a)^x＝((b/a)^x)^2 より、(b/a)^x＝(
＋１)/２よって、 x＝log((
＋１)/２)/log(b/a) により、（３）は、 log((
＋１)/２)/log(３/２) 、（４）は、log((＋１)/２)/log(４/３)しかし、（１）（２）は解ける方程式の形にならないので無理な気がします。
s(a^2)^x＋t(ab)^x＝u(b^2)^x
のように係数が掛かっていても解けますが、この形にもならないですよね。
以下、工事中！