
当HPがいつもお世話になっているA’zさんのHPと思われる掲示板で、やすさんという方
が平成19年11月6日付けで書き込みをされているのを拝見した。
A’zさんが考え方を説明されてはいるものの解答が完結していないと思い、問題自身の
面白さもあり、当HPで備忘録として残しておきたいという欲求にかられた。
正四面体を、底面に平行な n−1 枚の平面で、高さを n 等分するように切る。残
りの面に関しても同様に切ると正四面体はいくつの部分に分けられるか。その個数
を求めよ。
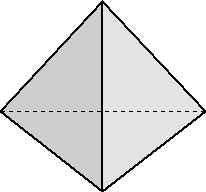
東工大のAO入試の問題とのことだが、中学で立体図形の切断が学習指導要領から削
除されて、生徒の立体把握の欠如に警鐘を鳴らす良問として取り上げた次第である。
n=2 のときの分割の様子を調べてみよう。
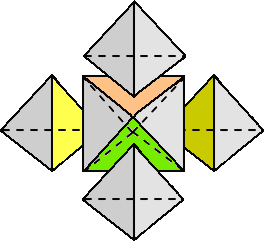
上図から、n=2 のときは、4つの正四面体と1つの正八面体に分割されるので、分割
の個数は、5個である。
この考察から、5個という個数は、次の正三角形の分割数の和に等しいことが分かる。
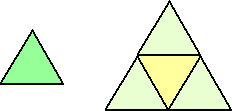
すなわち、 1+4=5 (個) となる。
3以上の n については、事はそう単純ではないということを、当HPがいつもお世話になっ
ている、らすかるさんからご指摘いただいた。
この問題について、ヨッシーさんが、HPサイト「数学の部屋」の掲示板(今はもう見れない?)
で考察されている。
ヨッシーさんの計算された結果によると、答えは
n(n2+1)/2
となるようだ。
(コメント) らすかるさん、ご指摘ありがとうございます。n=3 のときをもっと詳しく調べれ
ばよかったと後悔しています。A’zさん、これでいいんですよね?
ヨッシーさんの解法を参考にさせていただきながら、少し考察してみよう。
三角錐台の上面が左側の正三角形で、底面が右側の正三角形のとき、この操作で、
 三角錐台がいくつの部分に分けられるかを調
三角錐台がいくつの部分に分けられるかを調べることは大変興味深い問題である。
左側の正三角形の1個の面(正三角形そのもの)からは、1個の正八面体が派生し、3つ
の頂点からは、それぞれ正四面体が派生している。
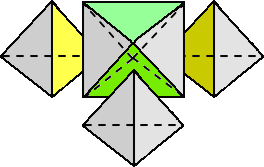
しかし、この見方でさらに修正が必要なことは、次の場合から明らかだろう。

左側の正三角形には、4個の面(正三角形)と6個の頂点があるので、三角錐台は4個の
正八面体と6個の正四面体が派生するはずであるが、実際には、そのようには分割されて
いない。
正四面体が7個と正八面体が3個である。
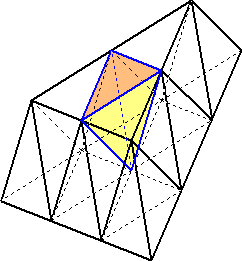
上向きの正三角形からは、正八面体が派生しているのだが、下向きの正三角形からは、
正八面体ではなく正四面体が派生している。
(空間で考えていると、上図の色付きの部分(三角錐)が忘れやすい...!)
したがって、上面の正三角形の各辺が k 等分されているときの三角錐台の分割数を求
めるには、上面の正三角形において、
頂点の数 、 上向きの正三角形の数 、 下向きの正三角形の数
を求めればよい。
頂点の数は、 1+2+3+・・・+(k+1)=(k+1)(k+2)/2 ・・・ 正四面体が派生
上向きの正三角形の数は、 1+2+3+・・・+k=k(k+1)/2 ・・・ 正八面体が派生
下向きの正三角形の数は、 (1+3+5+・・・+(2k−1))−k(k+1)/2
=k2−k(k+1)/2 ・・・ 正四面体が派生
以上から、正四面体、正八面体取り混ぜた分割数は、
(k+1)(k+2)/2+k(k+1)/2+k2−k(k+1)/2=(3k2+3k+2)/2
となる。
したがって、求める分割数は、 k=0、1、2、・・・、n−1 の各三角錐台の分割数の和を
求めればよいので、
となる。
(追記) 平成22年9月3日付け
この話題について、A.Y.さんという方からメールを頂いた。
具体的に、四面体、八面体を構成して考察されたという。
(参考ページ→) http://plaza.rakuten.co.jp/nisijohsyu/diary/201008310000/
※上記ブログの「前へ」をクリックすると関連話題が続きます。