平成１９年１０月１１日の午後３時〜午後３時半、ＮＨＫ高校講座「数学基礎」で秋山 仁
先生が面白い話題を提供された。
たとえば、次のような図形を考える。
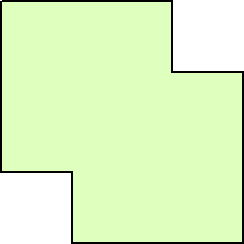正方形の折り紙に鋏を１回だけ入れて正確に左図のような図形を切り取るにはどうしたら
よいだろうか？
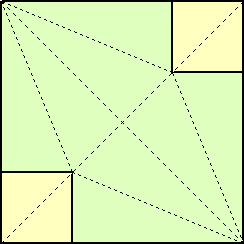
この問いに答えるには、正方形の折り紙に
左図のような折り目をつければ分かるだろう。
実際には、次のようにすればよい。
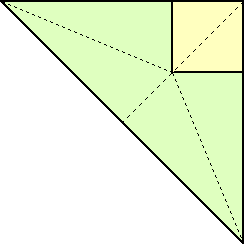
正方形の折り紙を左図のように対角線に沿
って折る。
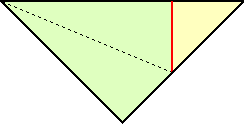再度残りの対角線に沿って折り、左図の赤線に沿って切り取れば、冒頭の図形が得られ
る。
以上の操作の基本的な原理は、角の２等分線と垂線の性質を用いる点である。
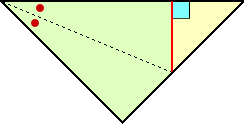
この原理を用いれば、三角形を正方形の折り紙に鋏を１回だけ入れて切り取ることも容
易だろう。
番組では、次の課題が出されていた。解答は示されなかったが、次のように考えればい
いのかな？
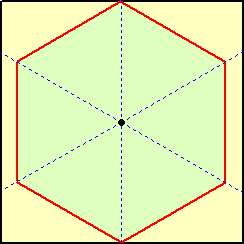
○ 正６角形を切り取る
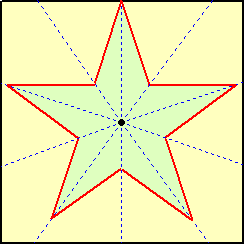
○ 星形を切り取る
（追記） 平成２６年１０月１０日付け
上記の事実は、「多角形の一刀切り」（江戸時代には、「一刀斬り」？）と言われる。
紙に書かれた多角形をハサミで切り取ることは易しい。この場合、ハサミは縦横無尽に紙
を切り取りながら動き回る。ハサミの向きを変えずに１回切るだけというのが、この「一刀切
り」のミソである。
すなわち、次の事実が知られている。
紙を上手く折り、ハサミの向きを変えずに一回切るだけで、任意の多角形が無限に
作れる
これを数学的に証明したのは、ＭＩＴの若き数学者エリック・ディメイン（Erik Demaine）である。
エリック・ディメインによれば、
切り出す図形において、それぞれの角の二等分線と、切り出す線に下ろした垂線を
折っていく。どれだけ複雑な形でも、多角形は最終的に三角形と四角形に分割できる。
さらに、折り目を追加すれば、三角形と四角形が一直線上に並ぶように折りたたむこ
とができる
という。
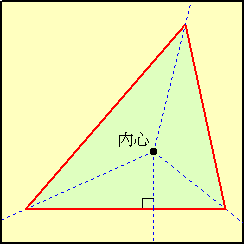
例 三角形の一刀切り
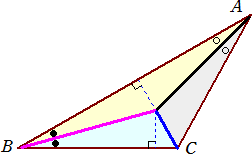
左図のような三角形を切り取りたい場合、
黒・青・紫の実線（角の２等分線）を山折り、内
心から辺に下ろした垂線を谷折りすれば、三角
形の３辺は同一直線上に重なり、従って一刀切
りが可能となる。
一刀切りをする際の基本的な方針は、
（１） 隣り合う２本の辺が作る角の２等分線を描く。
（２） 角が１８０°より小さければ、山折り、大きければ、谷折りにする。
読者のために、練習問題を残しておこう。
練習問題 数字の０から９までを一刀切りせよ。
（Ｈｉｎｔ） 易しい方から、 １ → ７ → ０ → ２ → ５ → ８ → ３ → ４ → ６（９）