
経験的に、我々が住む世界は3次元であることを、多分みんな知っている。高校で習う空間
座標を用いれば、3つの実数 a、b、c の組(a,b,c)により、空間の中の位置が確定するから
である。この場合、a、b、c は、全く自由に、その値をとることができ、自由度が3であること
から、3次元といわれる。
数学の場合、n 個の実数の組を用いれば、n 次元空間を表し、高次元に対しては、割と気楽に考えることができる。
もっとも、高次元では、常識では計り知れないこと(例えば、7次元エキゾチック球面の発見(ミルナー)・・・1956年)
も起こるし、高次元では証明済みなのが、4次元・5次元あたりでは、まだ証明されていないとか、数学者は、次元の
戯れによく翻弄される。
これに対して、空間のなかの平面、例えば、その方程式を、 Z=X+Y とすれば、X、Yは
自由に、その値をとることができるが、Zは、既に、X、Yに束縛されている。したがって、平面
の自由度は2で、2次元となる。同様に、空間内の直線、例えば、その方程式を、X=Y=−Z
とすれば、Z は自由に、その値をとることができるが、X、Y は既に、Z に束縛されている。
したがって、直線の自由度は1で、1次元となる。
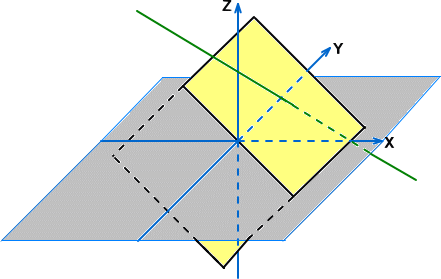
このように自由度により定まる次元の概念は、一般の人にとっても分かりやすい。
しかし、このごく自然とも思える次元の概念に対して、深刻な問題提起が、1890年になされた。
それは、ペアノ曲線などにより、2次元の平面である正方形上の任意の点が、1次元である
直線上の点(すなわち、1つの実数)で表されることが示されたからである。
ペアノ曲線の構成は、ヒルベルトにより、次のように説明されている。
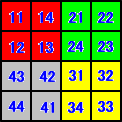
上図のように、正方形の各辺の等分を繰り返し、小正方形に分割する。この小正方形に適
切な方法により、番号をつける。この小正方形には、右上図の線分の同番号が対応する。
等分を無限回繰り返すことにより、正方形の各点と線分上の各点が対応することが分かる。
番号にしたがって、各小正方形を結んでいくと、線分との対応の状況が見えてくる。
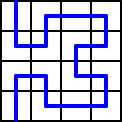
このような曲線の出現により、次元の定義が見直され、現在、種々の定義が考案されてい
る。(フラクタル次元、相似性次元、ハウスドルフ次元、容量次元、情報量次元、・・・)
フラクタル(Fractal)という言葉は、1975年、マンデルブロ(Mandelbrot)により作られた。
物が壊れて、小さな破片や大きな破片がたくさん集まったような状態を意味するらしい。
このフラクタルと密接な関係がある相似性次元について、次に考えてみよう。

1つの線分を、2等分すると、もとの線分と相似な線分が、2個できる。
正方形の各辺を2等分すると、もとの正方形と相似な正方形が4個できる。
このとき、
2=21 4=22
により、線分は、1次元、正方形は、2次元と定義するのが、相似性次元の考え方である。
これは、これまでの次元の概念と一致する。一般に、
ある図形が、nd 個の、全体を n 分の1 に縮小した図形で埋め尽くされるとき、
その図形は、d 次元(相似性次元)の図形であるという。
この次元によれば、ペアノ曲線は、2分の1に縮小した図形4個で埋め尽くされるので、
4=22 より、やはり、ペアノ曲線も、2次元の図形ということになり、正方形が2次元である
ことと矛盾しない。
しかし、この相似性次元の考えを認めると、実は驚くべき次元の図形が存在することにな
る。そのような例としては、次のような、コッホ曲線が有名である。
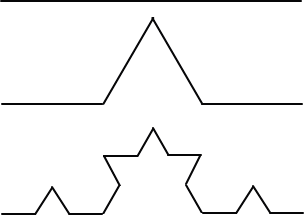
上図のように、1つの線分を3等分し、真ん中を山型に出っ張らせる。この操作を無限回
繰り返して得られる図形が、コッホ曲線である。
コッホ曲線は、全体を3分の1に縮小した相似図形4個で埋め尽くされる。
したがって、相似次元の計算によれば、求める次元 d は、
3d = 4
即ち、d = log34 ≒ 1.26・・・
となる。
小数次元というのは、はっきり言って、実感がわかない。しかし、もともとの空間における
自由度としての次元の呪縛から解き放たれて、次元というものを、その図形のもつ複雑さ
としての指標と考えれば、何となく雰囲気は伝わってきそうである。
コッホ曲線は、1次元である直線よりは、少し複雑で、先ほどの2次元であるペアノ曲線
ほどは複雑でない、という見方をすれば、あながち、1.26・・・次元というのも妥当な線か
な〜と、考えてしまう。
(参考文献:高安秀樹 著 フラクタル(朝倉書店)
辻 正次 著 集合論(共立出版))
(追記) 「次元の拡張の世界」と題して、当HPがいつもお世話になっているHN「GAI」さん
からご投稿いただきました。(平成27年11月2日付け)
位相次元では、1、2、3、4、・・・ の整数しかないが、フラクタルを考えるときは、ハウスドル
フ次元の非整数が入り込む。いろいろなフラクタルがどのような次元を持つのかを調べてみ
た。
<ハウスドルフ次元>:<フラクタル>
log[3]2=0.63093・・・ :カントール集合
log[3]3=1 :1次元(直線)
log[3]4=1.26186・・・ :コッホの雪、Cantor Dust
log[5]9=1.36521・・・ :ミンコフスキーのソーセージ
log[3]5=1.46497・・・ :Box Fractal
log[2]3=1.5849・・・ :シェルピンスキーのザル
log[3]8=1.89279・・・ :シェルピンスキーカーペット
log[3]9=2 :2次元(平面)
log[3]20=2.72683・・・ :メンガーのスポンジ
log[3]27=3 :3次元(空間)
*何方かlog[3]6、log[3]7次元のフラクタルの実例を御存知なら教えて下さい。
DD++さんからのコメントです。(平成27年11月2日付け)
log[3]6=1.630929754・・・ :Sierpinski hexagon
log[3]7=1.771243749・・・ :Hexaflake
です。多分...。
GAI さんからのコメントです。(平成27年11月2日付け)
なるほど、こんな図形であればいいのか!ありがとうございます。