
多変数関数の条件付き極値問題では、「ラグランジュの乗数」が活躍した。そこでは偏導
関数が生き生きとした素顔を覗かせてくれた。
自然科学では、運動方程式で代表されるように微分方程式で現象を考えるのが常道であ
る。私の高校時代の物理はまさに微分方程式の練習時間であり、当時は数学の延長程度
の認識だったが、今思うと、ごく自然な物理教程だったように感じる。
ただ、微分方程式を解くことは一般的に難しく、解けないときの方が多い。その場合は解
くことを諦めざるを得ず、微分方程式から得られる解の性質を追究することになる。
さらに、量子力学によれば、必ずしも微分方程式では自然現象すべてを表現できないとい
う。そうは言いつつも、やはり、微分方程式は自然現象を記述する数学として、それを学習
することの重要性は現在も失われていないと私は思う。
微分方程式が与えられたとき、あるいは作り出すとき、必ずと言っていいほど、偏微分方
程式を専門とする方は、それが意味する自然現象を常に意識されている。大学のお茶会
などで、専門的な話は分からないが、その点がいつも話題になっていたのが強く印象に残
る。
微分方程式といっても、常微分方程式は、ある意味で特殊である。たとえ注目する変数が
1つであっても時間の経過が入れば必然的に2変数の関数となるので、偏微分方程式を論
ずるのが自然であろう。
しかし、私自身正直に告白すると、これまでこれといった偏微分方程式を解いた経験がな
い。専門が代数系ということもあるが、偏微分することはあっても、偏微分方程式までは至
らなかった。
ところが、最近無性に偏微分方程式に愛着がわき起こり、基本的なものを解いてみたい
という欲求にかられた。そこで、このページを起こした次第である。
微分方程式を解くことはもちろん、微分方程式の背景にある自然現象にも是非目を向け
ていきたいと思う。
さて、いよいよ本論に入ろう。
関数 F( x , y ) に対して、偏微分の記号 Fx 、Fy 、Fxx 、Fxy 、Fyy 、・・・ が用いられる
が、私は、「∂」(←文字化けしてないかな?)を用いる偏微分の記号の方が好きだ!
偏微分方程式の解法を論ずる前に、いくつか代表的な偏微分方程式を作ってみよう。
例1
は、偏微分方程式 Fxx+Fyy+Fzz=0 を満たすことを示せ。
(解)
より、
同様にして、
よって、 Fxx+Fyy+Fzz=0 が成り立つ。 (終)
ここで、
を Laplace の演算子(Laplacian)という。
この記号を用いれば、上記例の偏微分方程式は、簡単に、 ΔF=0 と表される。
この微分方程式は、Laplaceの微分方程式と言われる。
また、 ΔF=0 の解 F を調和関数という。
複素数 z=x+i・y ( i は虚数単位)の複素数値関数
F(z)=u( x , y )+i・v( x , y )
が正則(regular)であるとき、Cauchy-Riemann の関係式
ux=vy 、 uy=−vx
が成り立つ。
このとき、 Δu=0 、 Δv=0 が成り立つことは自明だろう。
したがって、正則関数の実部、虚部は、調和関数と言える。
複素数 z=x+i・y に対して、共役複素数を
x=(z+
である。 よって、
から、
であることが分かる。 同様にして、
から、
であることが分かる。 このことから、
という関係が成り立つ。
この関係から、 Laplace の演算子の意味と重要性が頷ける。
例2 z=F(x2+y2) のとき、偏微分方程式 x・zy=y・zx を満たすことを示せ。
(解) u=x2+y2 とおくと、 z=F(u) である。
このとき、 zx=F’(u)・ux=2x・F’(u) 、 zy=F’(u)・uy=2y・F’(u)
よって、 x・zy−y・zx=2xy・F’(u)−2xy・F’(u)=0 より、
x・zy=y・zx
が成り立つ。 (終)
球面の上半面の方程式は、
により、球面の方程式は、偏微分方程式 x・zy=y・zx を満たす。
逆に、偏微分方程式 x・zy=y・zx を満たすとき、その曲面はどうなるのだろうか?
xy 平面に平行な平面上で考える。一般に、
が成り立つので、
という常微分方程式が得られる。これより、 2yy’=−2x なので、
(y2)’=−(x2)’ より、 y2=−x2+r2 すなわち、 x2+y2=r2
となり、z 軸上に中心を持つ円弧を表す。
この円弧の集合体として球面の上半面が構成される。

ある山に登るとき、登山者に対して、その付近の勾配の情報が次のように与えられるもの
とする。
東へ進むと、20mにつき 1m上がり、北へ進むと、15mにつき 1m上がる
このとき、その付近の曲面はどのような形になっているであろうか?言い換えれば、一番急
な上りの方向はどちらで、何mにつき何m上がるだろうか?
この問題は、偏微分係数の意味を理解する良問であり、偏微分方程式を解く上での指針
にもなり得る。
細実線を等高線とすれば、問題の意味は下図のように捉えられる。
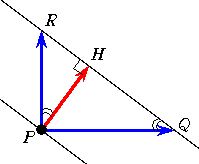
等高線による平面図を実際の立面図に翻訳すれば、山の勾配は下図のようになっている
ものと推察される。
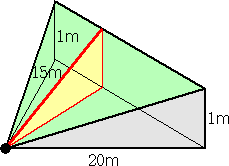
一番急な上りの方向を赤実線で表せば、 △PQR∽△HPR より、 PHは、12m進んで
1m上がる方向である。
これらのことを、偏微分係数を用いて表してみよう。
まず、東向きの条件は、 zx=1/20 北向きの条件は、 zy=1/15 となる。
このとき、等高線の向きは、 −15/20=−3/4 であるが、このことは、
が成り立つことを実証している。さらに、最大傾斜の方向は、4/3 であるが、これは、
により与えられる。
このように、x 軸方向、y 軸方向の偏微分係数が与えられると、その周辺での曲面の様子
が垣間見える。
常微分方程式で、y’=0 が最も簡単なものだろう。もう少しレベルアップして、y’=const.
も同程度だろうと思う。前者は定数関数で後者は1次関数となる。
それでは、偏微分方程式で最も簡単なものって何だろう。やはり、 zx=0 かな?
以下、工事中