
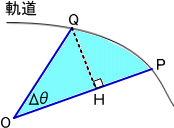
 軌道上のPの位置にあった惑星が、時間Δt の間にQまで移動し
軌道上のPの位置にあった惑星が、時間Δt の間にQまで移動し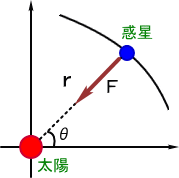
左図のように、太陽を原点とする直交座標系において、惑
星の位置を(X,Y)とする。惑星が太陽から受ける万有引力
をF、惑星の質量をm とすると、ニュートンの運動方程式から
![]()
が成り立つ。この2つの式から、Yを消去して、
![]()
ここで、
![]()
であるので、
![]()
がいえる。ただし、Cは任意定数。
このとき、X=rcosθ、Y=rsinθ を上式に代入して、
![]()
すなわち、
![]()
である。したがって、
![]()
が成り立ち、「惑星の面積速度は一定」であることが示された。