２．微分方程式を作る　　　　　　　　　　　　　　　　　　　

（１）　原点中心、半径ｒの円の曲線群の満たす微分方程式
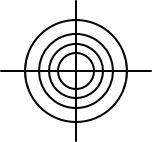
　　　Ｘ^２＋Ｙ^２＝ｒ^２　の両辺をＸで微分して、
　　　　　　　Ｘ＋ＹＹ’＝０　
　　　を得る。

　　　これは、接線方向を表すベクトル（１，Ｙ’）と半径方向を表すベクト
　　ル（Ｘ，Ｙ）の内積が０であることを示し、接点において接線と半径が
　　垂直であることが分かる。
　　　　　　　　　　　　　　　　　　　　　　

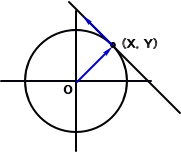
　微分方程式は、ｒを含まない式なので、全ての円に共通な性質
を表している。

（２）　原点を頂点とし、焦点（Ｐ，０）の放物線群の満たす微分方程式


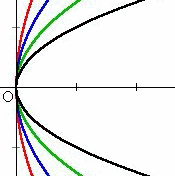
　　　 Ｙ^２＝４ＰＸ　の両辺をＸで微分して、２ＹＹ’＝４Ｐ で、
　　これを上式に代入すると、Ｙ^２＝２ＹＹ’Ｘ となるので、
　　　　　　２ＸＹ’−Ｙ＝０
　　を得る。

　　　これは、接点（Ｘ，Ｙ）における接線が左下図のような性質を有
　　することを意味する。



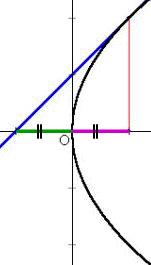　　　この性質を知っていれば、例えば、放物線Ｙ＝Ｘ^２上の点（１，１）
　　における接線の傾きが２であること、Ｙ切片の値が−１であること
　　が直ちに分かるので、接線の方程式は、Ｙ＝２Ｘ−１ となる。

　　　従来の微分係数を求める方法でもできるが、このような放物線
　　特有の性質に着目した解法は、とても美しい。










（３）　角速度ωの単振動
　　　Ｙ＝AsinωＸ　の両辺をＸで微分して、Ｙ’＝AωcosωＸ
　　この式の両辺をさらにＸで微分して、Ｙ”＝−Aω^２sinωＸ
　　従って、　　　Ｙ”＝−ω^２Ｙ
　　を得る。
　　　これは、直線上を運動する質点に対して原点からの距離に比例した大きさの、原点の
　　方に向いた力が働くことを表す。

　以上の例からも分かるように、図形の方程式をみても判然としない、その図形固有の性質
が、微分方程式を作ることにより浮かび上がってくるということに、とても新鮮な感動を覚える。
　次の章では逆に微分方程式を与えて、それを解く方法のいろいろを見てみることにしよう。