Ｙ’＝Ｘ　、　Ｙ’＝ＸＹ　、　Ｙ”＋Ｙ’＋Ｙ＝０　、　Ｙ”＋ω^２Ｙ＝sinＸ　、・・・
などのように、導関数Ｙ’、Ｙ”、・・・を含む等式を微分方程式という。特に、独立変数が１つのも
のを常微分方程式という。独立変数が２つ以上のものは、偏微分方程式といわれる。方程式に
含まれる導関数の階数の最大値を、その微分方程式の階数という。上記例のうち、１・２番目
のものは、１階常微分方程式、３・４番目のものは、２階常微分方程式である。
　１７世紀末〜１８世紀初め頃、ニュートン、ライプニッツにより微積分法が発見され、ニュートン
力学における運動方程式（加速度は力に比例する）が、微分方程式の始まりと言われている。
ニュートンは、Ｙ’＝Ｆ(Ｘ，Ｙ)の形を研究し、ライプニッツは、Ｙ’＝Ｆ(Ｘ)Ｇ(Ｙ)の形を研究したらし
い。
　与えられた微分方程式を満たす関数Ｙを、その微分方程式の解という。
微分方程式の解は、任意の定数Ｃ_１、Ｃ_２、・・・を含む式で与えられることが多い。このとき、解
のグラフ（解曲線）は、ある曲線群となる。任意定数を含む解を、一般解という。
　一般解の任意定数にある特定の値を代入することにより得られるような解を、特殊解という。
この解は、ある条件（初期条件）を満たす解でもある。
一般解の任意定数にどんな値を代入しても得られない解が存在する。このような解を、特異解
という。
（この特異解の定義は実は不正確である。はっきり定義することは実際のところ困難である。）

　微分方程式の一般解と特異解を求めることを、「微分方程式を解く」という。
微分方程式を解くといっても、次のような事実をわきまえていなければならない。
（１）　一般解と言えど、全ての解を表すものではないこと
（２）　平面上の任意の点を通る解曲線（ある初期条件を満たす解）はただ一つとは言えないこと

　微分方程式においては、次のことが問題になる。
（イ）　与えられた微分方程式には、解が存在するのか？
（ロ）　解が存在すれば、どのように求めればいいのか？
（ハ）　その解はどんな性質をもつのか？

上記の（イ）については、解の存在定理（後述）が知られている。また、（ロ）については、求積法
や級数展開法、演算子法など（後述）が知られるが、解の存在が分かっても、実際に解ける微分
方程式は、数少ない。一般的には、解けないものと思った方がいいだろう。（ハ）については、解
の安定性の問題（後述）などが大切なテーマとなる。

　次に、微分方程式と自然現象との関わり方について、いくつか例をあげよう。
例１．（ニュートンの運動方程式）
　　　　質量をｍ、力をＦで表せば、ｍＹ”＝Ｆ　　（Ｘ：時間）
例２．（単振動）
　　　　角速度をωで表せば、ｍＹ”＋ω^２Ｙ＝０　　　（Ｘ：時間）
例３．放射性物質は、時刻Ｘにおける質量Ｙに比例して減少する：Ｙ’＝−ｋＹ　　（ｋ：比例定数）
例４．（電気回路）

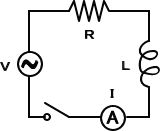
　　左図のような電気回路を考える。Ｘを時間とし、電圧Ｖ(Ｘ)、抵抗Ｒ
　（一定）、インダクタンスＬ（一定）、電流 I(Ｘ)　とすれば、キルヒホッフ
　の法則によって、次の微分方程式が成立する。
　　　　　　　　　　　Ｖ＝ＲI＋ＬI’



　このような微分方程式を解くことにより、物理現象が解明され、自然現象に近づく一歩となる。
微分方程式を解くことについては、また別の章で考えることにしよう。