
接線の問題は、平面幾何や解析等で話題になる常套問題である。このページでは、接線
に関連する問題を収集していこうと思う。
手頃な接線に関する問題が、東北大学 文系(1966)で出題されている。
問題 直線 y=2(x−1) が曲線 y=ax3+(1−2a)x (a≠0) に接するように a の値を
定めよ。
(解) 接点( t ,at3+(1−2a)t)における接線の方程式は、
y=(3at2+(1−2a))(x−t)+at3+(1−2a)t=(3at2+(1−2a))x−2at3
この式が y=2(x−1) と一致するので、 3at2+(1−2a)=2 、−2at3=−2
第2式より、 a=1/t3 で、これを第1式に代入して、 3/t−2/t3=1
よって、 t3−3t2+2=0 より、 (t−1)(t2−2t−2)=0 から、 t=1、1±
t=1 のとき、 a=1
t=1±
次のような解法も考えられる。
(別解) 題意より、 ax3+(1−2a)x=2(x−1) から、
ax3−(1+2a)x+2=a(x−α)2(x−β) と因数分解できる。
係数比較して、 2α+β=0 、−1−2a=a(α2+2αβ) 、2=−aα2β
β=−2α を第2式、第3式に代入して、 −1−2a=−3aα2 、1=aα3
a=1/α3 より、 −1−2/α3=−3/α から、 α3−3α2+2=0
よって、 α=1、1±
さらに、次のような解法も考えられる。
(別解) F(x)=ax3−(1+2a)x+2 とおくと、 F(x)=0 、F’(x)=0 は共通解を持つ。
F’(x)=3ax2−(1+2a)=0 から、a=1/(3x2−2)
よって、 x3/(3x2−2)−(1+2/(3x2−2))x+2=0 より、
x3−(3x2−2+2)x+2(3x2−2)=0 すなわち、 x3−3x2+2=0
よって、 x=1、1±
よおすけさんから問題をご提供いただきました。(令和6年7月8日付け)
問題 2つの2次関数 F(x)=−x2+2x−1、G(x)=x2 について、次の問いに答えなさい。
(1) 放物線 y=F(x) 上の点(a,−a2+2a−1)における接線の方程式を求めなさい。
(2) (1)の接線が放物線 y=G(x) にも接するように a の値を定めなさい。
(出典)第125回実用数学技能検定2級2次問題7
(解)(1) 接線の方程式は、y=(−2a+2)(x−a)−a2+2a−1=(−2a+2)x+a2−1
(2) x2=(−2a+2)x+a2−1 から、 x2+2(a−1)x−a2+1=0
判別式をDとすると、 D/4=(a−1)2+a2−1=2a2−2a=2a(a−1)=0
よって、 a=0、1 (終)
(追記) 令和6年9月29日付け
次の東北大学 理系(1981)の問題は漸化式を作って解く問題である。
問題4 数列 {an} を次のようにして定める。初項 a1 (a1≠0、a1≠2)は与えられた実数
である。次に、anが与えられたとき、曲線 y=1/x−1上に、x 座標がanである点Pをとる。
Pにおいて、この曲線に引いた接線が x 軸と交わる点をQとすると、Qの x 座標がan+1で
ある。(n=1、2、3、・・・)
(1) an+1−1とan−1との関係を調べよ。
(2) anをa1の式で表し、limn→∞ an を求めよ.
(解)(1) y’=−1/x2 なので、点Pにおける接線の方程式は、
y=−{1/an2}(x−an)+1/an−1=−{1/an2}x+2/an−1
y=0 とおいて、 x=2an−an2 より、 an+1=2an−an2
よって、 an+1−1=−(an−1)2
(2) an−1=−(an-1−1)2=−(an-2−1)4=・・・=−(a1−1)^(2n-1) (ただし、n≧2)
よって、 −1<a1−1<1 すなわち、 0<a1<2 のとき、an−1 → 0 (n → ∞)
a1<0 、2<a1 のとき、an−1 → −∞ (n → ∞)
したがって、 0<a1<2 のとき、limn→∞ an=1
a1<0 、2<a1 のとき、limn→∞ an=−∞ (終)
(追記) 令和6年11月30日付け
次の東北大学 理系(1987)の問題は、易しい問題だろう。
問題3 a を 0 でない実数とする。2つの曲線 y=ex および y=ax2 の両方に接する直線
の本数を求めよ。
(解) 曲線 y=ex 上の接点(t,et)における接線の方程式は、y=et(x−t)+et
これが、曲線 y=ax2 に接するので、 ax2=et(x−t)+et すなわち、
ax2−etx+(t−1)et=0 が重解を持つので、 (判別式)=e2t−4a(t−1)et=0
すなわち、 et=4a(t−1) において、 t≠1 なので、 a=et/(4(t−1))
y=et/(4(t−1)) のグラフは、y’=(t−2)et/(4(t−1)2) より、

したがって、 a<0 、a=e2/4 のとき、接線の本数は、1本
0<a<e2/4 のとき、接線の本数は、0本
a>e2/4 のとき、接線の本数は、2本 (終)
(追記) 令和7年3月27日付け
次の東北大学 後期文系(1990)の問題は、与えられた条件をどう使うのかがポイントだ
ろう。
問題 xy平面の原点をO、放物線 y2=x 上の点をP、放物線 y=x2 上の点をQ、Qにお
ける y=x2 の接線と x 軸の交点をRとする。PとQをP≠O、Q≠O、OP⊥OQとなるよ
うに動かし、位置ベクトルORをOR=pOP+qOQ (p、q は実数) と表す。
pとqの関係を求め、点(p,q)の描く図形をかけ。
(解) P(t2,t)、Q(s,s2) とおくと、OP⊥OQより、 st2+s2t=0 なので、t+s=0
よって、Q(−t,t2) と書ける。 y’=2x より、Qにおける接線の方程式は、
y=−2t(x+t)+t2=−2tx−t2 となるので、y=0 とおいて、 x=−t/2
よって、R(−t/2,0) となる。
OR=pOP+qOQ (p、q は実数) より、
(−t/2,0)=p(t2,t)+q(−t,t2) すなわち、 pt2−qt=−t/2 、pt+qt2=0
t≠0 なので、 pt=q−1/2 、p+qt=0
t=−p/q を第1式に代入して、 −p2/q=q−1/2 すなわち、 p2+q2−(1/2)q=0
より、 p2+(q−1/4)2=1/16
よって、点(p,q)は、中心(0,1/4)で半径1/4の円周上にある。ただし、p≠0 より、
(0,0)、(0,1/2)は除く。
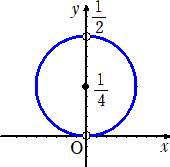 (終)
(終)(追記) 令和7年4月8日付け
次の東北大学 後期理系(1991)の問題は、与えられた条件をどう使うのかがポイントだ
ろう。
問題 傾きが正の直線Lが2つの放物線
C1:y=ax2+1/(3a3) 、C2:y=bx2+1/(3b3) (a>0、b>0、a≠b)
に接している。このとき、次の問に答えよ。
(1) LとC1の接点を(p,q)とするとき、p、q を a、b を用いて表せ。
(2) X=limb→a p、Y=limb→a q とする。X、Yを求め、さらにYをXの式で表せ。
(3) a が正の実数全体を動くとき、点(X,Y)を描く曲線の概形をかけ。
(解)(1) y’=2ax より、(p,q)における接線の方程式は、
y=2ap(x−p)+q=2apx−2ap2+ap2+1/(3a3)=2apx−ap2+1/(3a3)
y=bx2+1/(3b3) と連立して、 bx2−2apx+ap2−1/(3a3)+1/(3b3)=0
接することから、判別式D/4=a2p2−abp2+b/(3a3)−1/(3b2)=0
よって、 a(a−b)p2=1/(3b2)−b/(3a3)=(a−b)(a2+ab+b2)/(3a3b2) より、
p2=(a2+ab+b2)/(3a4b2) から、 p=(√(a2+ab+b2))/(
また、 q=ap2+1/(3a3)=(a2+ab+2b2))/(3a3b2)
(2) b→a のとき、
X=limb→a (√(a2+ab+b2))/(
Y=limb→a (a2+ab+2b2))/(3a3b2)=4/(3a3)
なので、 Y=(4/3)X^(3/2) (X>0)
(3) 点(X,Y)を描く曲線の概形は、
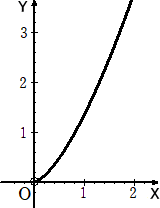 (終)
(終)(追記) 令和7年5月23日付け
次の東北大学 後期文系(1993)の問題は、接線の計算である。
問題 曲線C: y=x3−(1+t)x2+(t−2)x+2t を考える。ただし、t は −1<t<2 を満
たす定数とする。点(−1,0)を通り、Cに接する直線の1つをL、点(2,0)を通り、Cに接す
る直線の1つをKで表す。L‖Kとなるような t、L、Kを求めよ。
(解) L、KとCとの接点の x 座標を、それぞれ a、b とおく。
y’=3x2−2(1+t)x+t−2 で、L‖Kより、
3a2−2(1+t)a+t−2=3b2−2(1+t)b+t−2 すなわち、 3(a+b)=2(1+t)
Lの方程式は、
y=(3a2−2(1+t)a+t−2)(x−a)+a3−(1+t)a2+(t−2)a+2t
点(−1,0)を通るので、
(3a2−2(1+t)a+t−2)(−1−a)+a3−(1+t)a2+(t−2)a+2t=0
すなわち、 −2a3+(t−2)a2+2(1+t)a+t+2=0
このとき、 (a+1)2(−2a+t+2)=0 より、 a=−1、(t+2)/2
Kの方程式は、
y=(3b2−2(1+t)b+t−2)(x−b)+b3−(1+t)b2+(t−2)b+2t
点(2,0)を通るので、
(3b2−2(1+t)b+t−2)(2−b)+b3−(1+t)b2+(t−2)b+2t =0
すなわち、 −2b3+(t+7)b2−4(1+t)b+4t−4=0
このとき、 (b−2)2(−2b+t−1)=0 より、 b=2、(t−1)/2
(イ) a=−1、b=2 のとき、 2(1+t)=3(a+b)=3 から、 t=1/2
接線の傾き 3a2−2(1+t)a+t−2=3+3−3/2=9/2
よって、 L:y=(9/2)(x+1) 、K:y=(9/2)(x−2)
(ロ) a=−1、b=(t−1)/2 のとき、 2(1+t)=3(a+b)=3(t−3)/2 から、
t=−13 これは、−1<t<2 から不適。
(ハ) a=(t+2)/2、b=2 のとき、 2(1+t)=3(a+b)=3(t+6)/2 から、
t=14 これは、−1<t<2 から不適。
(ニ) a=(t+2)/2、b=(t−1)/2 のとき、 2(1+t)=3(a+b)=3(2t+1)/2 から、
t=1/2 で、このとき、a=5/4 、b=−1/4 なので、
接線の傾き 3a2−2(1+t)a+t−2=75/16−15/4−3/2=−9/16
よって、 L:y=−(9/16)(x+1) 、K:y=−(9/16)(x−2) (終)
(追記) 令和7年6月20日付け
次の東北大学 前期文系(1995)の問題は、接線のなす角の計算である。
問題 放物線C:y=(x2+3)/2 上に2点A(a,(a2+3)/2)、B(b,(b2+3)/2) (a<b)
をとる。AにおけるCの接線と、BにおけるCの接線の交点をPとする。
(1) Pの座標を a、b を用いて表せ。
(2) ∠APB=45°のとき、a と b の関係式を求めよ。
(3) ∠APB=45°という関係を満たすようにA、Bを動かすとき、Pの軌跡を求め、それを
図示せよ。
(解)(1) y’=x より、AにおけるCの接線の方程式は、
y=a(x−a)+(a2+3)/2=ax−(a2−3)/2
同様に、BにおけるCの接線の方程式は、
y=b(x−b)+(b2+3)/2=bx−(b2−3)/2
ax−(a2−3)/2=bx−(b2−3)/2 より、 (a−b)x=(a−b)(a+b)/2
a≠b より、 x=(a+b)/2
このとき、 y=a(a+b)/2−(a2−3)/2=(ab+3)/2 なので、Pの座標は、
P((a+b)/2,(ab+3)/2)
(2) Aにおける接線が x 軸の正の向きとなす角をα、Bにおける接線が x 軸の正の向き
となす角をβとおくと、条件より、 α=β+45° が成り立つ。このとき、
tan45°=tan(α−β)=(tanα−tanβ)/(1+tanαtanβ)=1
すなわち、 (a−b)/(1+ab)=1 より、 ab+1=a−b<0
(3) X=(a+b)/2 、Y=(ab+3)/2 とおくと、(ab+1)2=(a−b)2=(a+b)2−4ab
よって、 (2Y−2)2=(2X)2−4(2Y−3) より、 X2−Y2=−2
ただし、 2Y−2<0 より、 Y<1 である。
求めるPの軌跡は、下図。
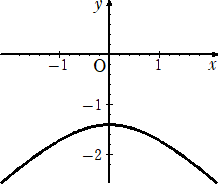
(追記) 令和7年6月24日付け
次の東北大学 後期理系(1995)の問題は、法線に関する問題である。
問題 放物線 y=(1/2)x2−1 上の点T(t,(1/2)t2−1)における法線をLtとする。
(1) Ltが点P(p,q)を通るとき、p、q、t の満たす関係式を求めよ。
(2) 点P(p,3/2)を通る法線Ltの本数について調べよ。
(3) 点P(p,q)を通る法線Ltがちょうど2本あるとき、p と q の満たす関係式を求めよ。
(解)(1) y’=x で、t≠0 のとき、点Tを通る法線の方程式は、
y=(−1/t)(x−t)+(1/2)t2−1=(−1/t)x+(1/2)t2
点P(p,q)を通るので、 q=(−1/t)p+(1/2)t2 すなわち、 t3−2qt−2p=0
ここで、t=0 のときの法線の方程式は、 x=0 で、点P(p,q)を通るから、 p=0
これは、t3−2qt−2p=0 において、t=0 として得られる。
以上から、すべての実数 t に対して、p、q、t の満たす関係式は、t3−2qt−2p=0
(2) q=3/2 のとき、 t3−3t−2p=0 すなわち、 t3−3t=2p
y=t3−3t とおくと、 y’=3t2−3=3(t+1)(t−1)=0 より、 t=±1
t=−1 のとき、極大で、極大値 2
t=1 のとき、極小で、極小値 −2
したがって、 2p<−2、2p>2 すなわち、 p<−1、p>1 のとき、法線は1本引ける。
p=±1 のとき、法線は2本引ける。
−1<p<1 のとき、法線は3本引ける。
(3) 題意より、 t3−2qt=2p が実数解を2個持てばよい。
y=t3−2qt とおくと、 y’=3t2−2q=0 より、 t2=(2/3)q
実数解を2個持つためには、極値を持つ必要があるので、 q>0 でなければならない。
このとき、 t=±√{(2/3)q} から、極値は、 ±(4/3)q√{(2/3)q}
よって、実数解を2個持つためには、 ±(4/3)q√{(2/3)q}=2p すなわち、
27p2=8q3 、q>0 (終)
(追記) 令和7年9月3日付け
次の東北大学 後期理系(1998)の問題は、基本問題であろう。
問題 (1) xy平面上の原点Oと異なる点Pに対し、OP=(rcosθ,rsinθ) (r>0) とす
る。点Pを通り、ベクトルOPに直交する直線の方程式を求めよ。
(2) 楕円 x2/a2+y2/b2=1 (a,b>0) の任意の接線に、原点Oから下した垂線をOPと
する。また、ベクトルOPに対し、r、θを(1)のように定義する。このとき、r をθで表せ。
(解)(1) rcosθ(x−rcosθ)+rsinθ(y−rsinθ)=0 より、 xcosθ+ysinθ=r
(2) 接点(acosφ,bsinφ)における接線の方程式は、 xcosφ/a+ysinφ/b=1
(1)で求めた直線 xcosθ+ysinθ=r すなわち、 xcosθ/r+ysinθ/r=1 と一致す
るので、 cosφ/a=cosθ/r 、sinφ/b=sinθ/r
よって、 rcosφ=acosθ 、rsinφ=bsinθ より、 r2=a2cos2θ+b2sin2θ
すなわち、 r=√(a2cos2θ+b2sin2θ) (終)
(追記) 令和7年11月7日付け
次の東北大学 前期理系(2002)の問題は、基本問題であろう。
問題 a>b>0 とし、xy平面の楕円 x2/a2+y2/b2=1 の第1象限の部分をEとする。
ただし、第1象限には x 軸と y 軸は含まれない。E上の点PにおけるEの接線と法線が
y 軸と交わる点の y 座標をそれぞれ h と k とし、L=h−k とおく。点PがE上を動くとき、
Lの最小値が存在するための a と b についての条件と、そのときのLの最小値を求めよ。
(解) P(s,t)における接線の方程式は、 sx/a2+ty/b2=1 すなわち、
y=−sb2/(ta2)・x+b2/t
よって、 h=b2/t
P(s,t)における法線の方程式は、y=ta2/(sb2)・(x−s)+t なので、 k=t−ta2/b2
よって、 L=b2/t−t+ta2/b2=(a2−b2)t/b2+b2/t (0<t<b)
L’=(a2−b2)/b2−b2/t2={(a2−b2)t2−b4}/(b2t2)
よって、a2−b2≦0 のとき、 L’<0 となり、Lは単調に減少し、最小値を持たない。
したがって、最小値を持つためには、 a2−b2>0 でなければならない。
このとき、0<t<b の範囲で、t=b2/√(a2−b2) のとき、極小かつ最小となればよいので、
b2/√(a2−b2) <b すなわち、 a>
このとき、 最小値は、 2√(a2−b2) である。 (終)
(追記) 令和7年11月20日付け
次の東北大学 後期文系(2002)の問題は、煩雑で計算の方向性を見失いそうである。
問題 2つの放物線 C1:y=x2 、C2:y=(x−a)2+b (a≠0) と1点ずつを共有する
放物線 C:y=p(x−q)2+r (p≠1) を考える。CiとCの共有点をPi(xi,yi)とする。
このとき、x1≠x2であることを示せ。さらに、線分P1P2の傾きを a、b のみの式で表せ。
(解) 題意より、P1は、C1とCの接点、P2は、C2とCの接点である。
よって、 2x1=2p(x1−q) 、2(x2−a)=2p(x2−q) から、
x1=pq/(p−1) 、x2=(pq−a)/(p−1)
このとき、 x1−x2=a/(p−1)≠0 から、 x1≠x2である。
y1=p2q2/(p−1)2
y2=((pq−a)/(p−1)−a)2+b=p2(q−a)2/(p−1)2+b
より、 y2−y1=p2(a2−2aq)/(p−1)2+b
p2q2/(p−1)2=p(pq/(p−1)−q)2+r =pq2/(p−1)2+r より、 r=pq2/(p−1)
((pq−a)/(p−1)−a)2+b=p((pq−a)/(p−1)−q)2+r より、
p2(q−a)2/(p−1)2+b=p(q−a)2/(p−1)2+r=p(q−a)2/(p−1)2+pq2/(p−1)
なので、
b=p(q−a)2/(p−1)2+pq2/(p−1)−p2(q−a)2/(p−1)2=p(2qa−a2)/(p−1)
以上から、
y2−y1=p2(a2−2aq)/(p−1)2+p(2qa−a2)/(p−1)
=p2(a2−2aq)/(p−1)2−p(p−1)(a2−2aq)/(p−1)2=p(a2−2aq)/(p−1)2
なので、 (y2−y1)/(x2−x1)=p(2q−a)/(p−1)=b/a となる。 (終)
(コメント) 煩雑な計算でしたが、結果は「美しい!」ですね。
以下、工事中!