嬤帡偵偮偄偰丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂摉俫俹偱偼丄偄傠偄傠側抣傪庤寁嶼偱媮傔傞曽朄傪偄偔偮偐徯夘偟偰偒偨丅
丂暯曽崻丒棫曽崻傪昅嶼偱媮傔傞曽朄偵偮偄偰丄丄庤寁嶼偑柺敀偄丄曽掱幃偵傛傞奐暯丄
丂柍棟悢傪嬤帡偡傞暘悢丄挻墇悢傪庤寁嶼偱媮傔傞丄暯曽崻俀傪媮傔傞悢楍丄
丂崅師曽掱幃偺夝偺嬤帡寁嶼丄丒丒丒丒丒丒丒丒丒丒丒丒
丂傕偪傠傫忋婰偺傛偆側寁嶼偼戝愗偱偁傞偑丄偪傚偭偲晄枮傕偁偭偨丅偦傟偼丄庤寁嶼偲偄偭
偰傕寢峔側寁嶼偑昁梫偩偲偄偆偙偲偱偁傞丅
丂悢偺偍傛偦偺抣傪帺椡偱寁嶼偡傞偲偄偆庯巪偼払惉偟偰偄傞偑丄偦偺偍傛偦偺抣傪懄嵗
偵埫嶼偵嬤偄宍偺娙扨側寁嶼偱媮傔偨偄偲偄偆婓朷偼姁偭偰偄側偐偭偨丅
丂偦偙偱丄偙偺儁乕僕偱偼丄埫嶼偺儗儀儖偱悢偺偍傛偦偺抣傪媮傔傞偲偄偆億儕僔乕偺傕偲偵丄
偄偔偮偐偺榖戣傪傑偲傔傛偆偲巚偆丅
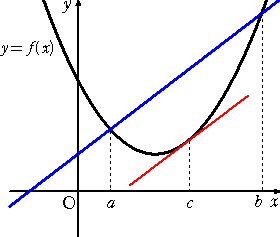
丂偙偺応崌偺崻掙偵側傞掕棟偑丄暯嬒抣偺掕棟偱偁傞丅
暯嬒抣偺掕棟
丂娭悢 倖 (倃) 偑丄嬫娫 乵 倎 丆 倐 乶 偱楢懕偱丄嬫娫 乮 倎 丆 倐 乯 偱旝暘壜擻偱偁傞偲偒丄
丂f (倐) 亖 倖 (倎) 亄 乮 倐 亅 倎 乯倖乫(們)丂丂丂乮丂倎 亙 們 亙 倐丂乯
傪枮偨偡 們 偑彮側偔偲傕堦偮懚嵼偡傞丅
丂偙偺掕棟偼丄師偺傛偆側宍偵曄宍偟偰峫偊傞偲丄堄枴偑暘偐傝傗偡偄丅
 |
丂丂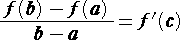
丂丂丂嵍曈偼丄俀揰乮倎丆倖(倎)乯丄乮倐丆倖(倐)乯 傪捠傞
丂丂捈慄偺孹偒偱偁傝丄
丂丂丂偦偺孹偒偵摍偟偄旝暘學悢偑懚嵼偡傞
丂丂偲偄偆偙偲傪暯嬒抣偺掕棟偼庡挘偟偰偄傞丅 |
丂偲偙傠偱丄乽旝暘壜擻乿偲偄偆尵梩偵偮偄偰丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞枹嵷幚偝傫
偺俫俹乽悢棟僷僘儖擖栧乿偱榖戣偵側偭偰偄偨丅枹嵷幚偝傫偺愢柧偑堦斣暘偐傝傗偡偄偲巚
偄傑偟偨丅丏丏丏丏丏丏丏丏乮偪傚偭偲婥偵側偭偨傕偺偱両尰嵼儕儞僋愗傟偱垼偟偄両乯
丂暯嬒抣偺掕棟偵偍偄偰丄倐 偑廫暘 倎 偵嬤偄偲偒丄摉慠 們 傕廫暘 倎 偵嬤偄丅
偙偺偙偲偐傜丄倐亖倎亄倛丂偲偟偰丄倛佮侽丂偺偲偒丄師偺傛偆側侾師嬤帡幃傪摼傞丅
丂f (倎亄倛) 佮 倖 (倎) 亄 倛倖乫(倎)
丂偙偺侾師嬤帡幃偼丄彮乆嬤帡偺巇曽偑慹偭傐偄報徾傪庴偗傞偑丄幚偼堄奜偵傕幚梡揑
偵偼廫暘偡偓傞椙岲側嬤帡傪梌偊傞丅
椺丂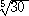 偺偍傛偦偺抣傪媮傔傛丅
偺偍傛偦偺抣傪媮傔傛丅
丂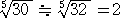 丂丂側偺偱丄
丂丂側偺偱丄
丂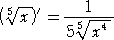
偵拲堄偟偰丄
丂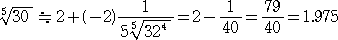
丂揹戩傪梡偄偰丄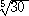 丂偺抣傪媮傔偰傒傟偽丄侾丏俋俈係俁俆丒丒丒丂側偺偱丄彫悢戞俀埵傑偱怣
丂偺抣傪媮傔偰傒傟偽丄侾丏俋俈係俁俆丒丒丒丂側偺偱丄彫悢戞俀埵傑偱怣
棅偱偒傞丅乮忋婰偺寁嶼偑埫嶼偱偱偒傞偐偳偆偐偼屄乆恖偺寁嶼擻椡偵傛偭偰嵍塃偝傟傞丅乯
丂忋婰偺媮傔曽偵懳偟偰丄師偺傛偆側媮傔曽乮娭悢幃偺愝掕偺堘偄乯傕偁傞丅
丂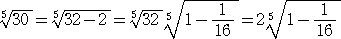
傑偨丄娭悢丂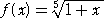 丂偵懳偟偰丄
丂偵懳偟偰丄
丂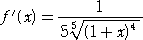
側偺偱丄丂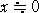 丂偺偲偒丄
丂偺偲偒丄
丂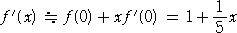
偑惉傝棫偮丅偙偺偲偒丄
丂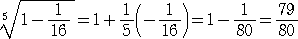
傛偭偰丄
丂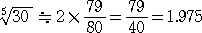
丂巹屄恖揑偵偼丄埫嶼偺儗儀儖偱悢偺偍傛偦偺抣傪媮傔傞偲偄偆庯巪偵徠傜偣偽丄慜幰偺
曽偑夝摎偲偟偰幚愴揑偱偁傞偲巚偆偺偩偑丄撉幰偺奆偝傫偼偳偆姶偠傜傟傞偱偁傠偆偐丠
乮捛婰乯丂値 忔崻偺嬤帡寁嶼偵偮偄偰丄俫俹 丗 乽崅峑悢妛偺憢乿偺拞偺丄椦丂朚塸偝傫偺儗億
丂丂丂乕僩偑戝偄偵嶲峫偵側偭偨丅
丂儗億乕僩偵傛傞偲丄丂倎 佮 侾 偺偲偒丄師偺嬤帡幃
丂
偑惉傝棫偮偲偄偆丅帋偟偵丄丂値 亖 俆 丄 倎亖侾俆/侾俇丂偲偟偰丄岞幃傪揔梡偟偰傒傞偲丄
丂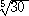 佮 俀丒乮俇丒乮侾俆/侾俇乯亄係乯/乮係丒乮侾俆/侾俇乯亄俇乯亖 俈俈/俁俋佮 侾丏俋俈係俁俆俉俋俈係俁俆丒丒丒
佮 俀丒乮俇丒乮侾俆/侾俇乯亄係乯/乮係丒乮侾俆/侾俇乯亄俇乯亖 俈俈/俁俋佮 侾丏俋俈係俁俆俉俋俈係俁俆丒丒丒
丂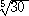 丂偺抣偼丄侾丏俋俈係俁俆侽係俉俇丒丒丒丂側偺偱丄彫悢戞俆埵傑偱惓偟偔媮傔傜傟偰偄傞丅
丂偺抣偼丄侾丏俋俈係俁俆侽係俉俇丒丒丒丂側偺偱丄彫悢戞俆埵傑偱惓偟偔媮傔傜傟偰偄傞丅
丂偙偺帠忣傪僌儔僼傪捠偟偰峫嶡偟偰傒傛偆丅
丂俀偮偺娭悢丂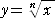 丂偲丄 丂偲丄 |
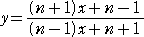 |
丂偼丄揰乮侾丆侾乯偵偍偄偰丄嫟捠偺愙慄 |
丂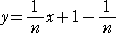
傪桳偡傞丅偟偨偑偭偰丄丂倶 佮 侾 偺偲偒丄
丂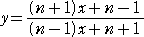 丂 丂 |
偲丂 |
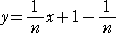 |
偼丄椉幰偲傕丄丂 丂偺嬤帡傪梌偊偰偄傞偙偲偑暘偐傞丅
丂偺嬤帡傪梌偊偰偄傞偙偲偑暘偐傞丅
偟偐傞偵丄
丂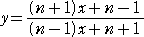
偺曽偑丄傛傝傛偄嬤帡傪梌偊偰偄傞偙偲偑丄壓恾偐傜椆夝偝傟傞丅
丂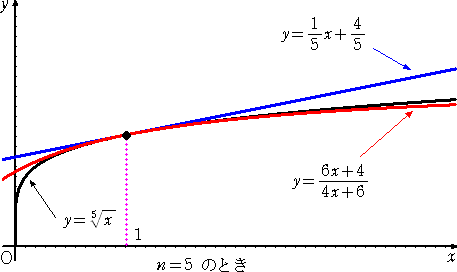
乮僐儊儞僩乯丂庤寉偵丄惛搙傛偔丄椵忔崻偺嬤帡抣偑媮傔傜傟傞偙偲偵丄偲偰傕姶摦偟傑偟偨両
丂丂丂丂丂椦偝傫偵姶幱偟傑偡丅乯
乮捛婰乯丂暯惉侾俋擭侾寧俇擔晅偗
丂忋婰偺榖戣偵娭楢偟偰丄侾寧俆擔晅偗偱丄俫俶乽揹戩抝乿偝傫偑摉俫俹偺宖帵斅乽弌夛偄偺愹乿
偵師偺傛偆偵彂偒崬傒傪偝傟偨丅
丂愄僽儖乕僶僢僋僗偺杮偱丄揹戩偱値忔崻偺嬤帡傪媮傔傞曽朄傪撉傫偩偙偲偑偁傞偺偱偡偑丄
尨棟偑傛偔傢偐傝傑偣傫丅偨偟偐偵偐側傝椙偄嬤帡偑摼傜傟傞偺偱偡偑丄尨棟偑傢偐傞曽丄嫵
偊偰偔偩偝偄丅
丂偙偺儁乕僕偱徯夘偟偨丄椦丂朚塸偝傫偺寢壥傪梡偄傞偲丄乽揹戩抝乿偝傫偑媮傔偰偄傞尨棟
偑愢柧偱偒偦偆偱偁傞丅
丂偡側傢偪丄
丂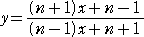 |
丂偑丄 |
 |
丂偺嬤帡傪梌偊偰偄傞偙偲傪棙梡偟偰丄堦斒 |
偺悢 俙丂偵懳偟偰丄偦偺 値 忔崻偺嬤帡抣偑併婡擻晅偒偺晛捠偺揹戩偱媮傔傜傟傞丅
丂乽揹戩抝乿偝傫偵傛傟偽丄師偺傛偆偵傗傟偽傛偄偲偺偙偲偱偁傞丅
乮弌揟偼丄島択幮偺僽儖乕僶僢僋僗乯
亙亙晛捠揹戩偱 俙 偺 値 忔崻傪媮傔傞庤弴亜亜
乮侾乯丂揹戩偱丄悢 俙丂乮偨偲偊偽丄俙亖俁 乯傪懪偪崬傓丅乮仺丂乽俁乿丂乯
乮俀乯丂乽併乿僉乕傪俉夞墴偡丅
乮仺丂偙偺憖嶌偱丄尷傝側偔 侾 偵嬤偄抣傪媮傔傞丅悢 俙偑偁傞掱搙戝偒偄悢偺応崌偼丄併僉
丂乕傪墴偡夞悢傪憹傗偝側偗傟偽側傜側偄丅乯
乮俁乯丂侾 傪壛偊偰丄儊儌儕偵曐懚乮仺丂乽亄乿乽侾乿乽俵亄乿丂乯
乮係乯丂悢 俀 傪乮俁乯偺抣偱妱偭偰丄侾 傪堷偔丅乮仺丂乽俀乿乽亐乿乽俵俼乿乽亅乿乽侾乿乽亖乿丂乯
乮俆乯丂乮寁嶼偡傞 値 忔崻偺 値 偺抣傪丄偨偲偊偽丄値亖俈丂偲偟偰乯
丂乮係乯偺抣傪 俈 偱妱傝丄侾 傪壛偊丄乮俁乯偺儊儌儕傪僋儕傾偟偰偐傜丄儊儌儕偵曐懚丅
丂乮仺丂乽亐乿乽俈乿乽亄乿乽侾乿乽俵俠乿乽俵亄乿丂乯
乮俇乯丂悢 俀 傪乮俆乯偺抣偱妱偭偰丄侾傪堷偔丅乮仺丂乽俀乿乽亐乿乽俵俼乿乽亅乿乽侾乿乽亖乿丂乯
乮俈乯丂乽亊乿僉乕偲乽亖乿僉乕傪 侾 僙僢僩偲偟偰丄乮俀乯偲摨偠夞悢傪墴偡丅
乮仺丂乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿丂乯
乮曗懌乯丂暯惉侾俋擭侾寧侾侽擔晅偗偱乽揹戩抝乿偝傫偐傜丄堦斒揑側揹戩偱偼丄
丂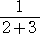
偲偄偆寁嶼偼丄丂乽俀乿乽亄乿乽俁乿乽亐乿乽亖乿乽侾乿乽亖乿丂偲偄偆憖嶌偱媮傔傜傟傞傕偺偑懡偄偲
偺偛嫵帵傪偄偨偩偄偨丅
丂巹偺垽梡偡傞揹戩乮悘暘愄偵丄俿倕倶倎倱丂俬値倱倲倰倳倣倕値倲倱 幮偐傜偺傕傜偄暔丏丏丏乯偱偼巆擮側偑傜弌棃側
丂丂
偐偭偨偑丄嵟嬤傕傜偭偨暿側揹戩偱偼妋偐偵弌棃偨偺偱丄悘暘揹戩傕恑曕偟偨傕偺偩偲姶怱
偟偨丅偦傟偵偟偰傕丄巹偑忋婰偺揹戩偲摨條偺婡擻傪帩偮戩忋寁嶼婡乮崱偱傕尰栶両乯傪峸
擖偟偨崰偼丄俀乣俁枩墌乮摉帪偺嬥妟偱両両乯偲崅壙側報徾偑偁偭偨偑丄嵟嬤偼丄揹戩偑柍
椏偱傕傜偊傞帪戙偵側偭偰偟傑偭偨両
丂乽俀乿乽亄乿乽俁乿乽亐乿乽亖乿乽侾乿乽亖乿丂偺偆偪慜敿偺丂乽俀乿乽亄乿乽俁乿乽亐乿乽亖乿丂偱偼丄
丂乽俀亄俁乿偺寁嶼寢壥偺媡悢乽侽丏俀乿傪寁嶼偟丄屻敿偺丂乽侾乿乽亖乿丂偱偼丄偦偺寁嶼寢壥偺
乽侾乿攞丂傪媮傔傞偲偄偆僇儔僋儕偵側偭偰偄傞傛偆偩丅
丂乽揹戩抝乿偝傫偵傛傟偽丄偙偺僇儔僋儕傪梡偄傞偲丄忋婰偺乮侾乯乣乮俈乯偱峴偭偨寁嶼偼丄幚嵺
偵揹戩偺僉乕傪偨偨偔応崌丄師偺傛偆偵憖嶌偡傞偲偺偙偲偱偁傞丅
丂乽俁乿
丂乽併乿乽併乿乽併乿乽併乿乽併乿乽併乿乽併乿乽併乿丂乮仼丂併傪丄俉夞乯
丂乽亄乿乽侾乿乽亐乿乽亖乿乽俀乿乽亖乿
丂乽亅乿乽侾乿
丂乽亐乿乽俈乿
丂乽亄乿乽侾乿乽亐乿乽亖乿乽俀乿乽亖乿
丂乽亅乿乽侾乿
丂乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿乽亊乿乽亖乿丂乮仼丂暯曽偺寁嶼傪丄俉夞乯
幚嵺偵丄偙偺曽朄偱丄俁 偺 俈 忔崻偺嬤帡抣傪媮傔偰傒傞偲丄侾丏侾俇俋俋俁侽俆俁俈丂偲側傝丄幚
嵺偺抣乮侾丏侾俇俋俋俁侽俉侾俁乯偲斾傋偰傕側偐側偐偺惛搙偲偺偙偲偱偁傞丅
乮僐儊儞僩乯丂昞寁嶼僜僼僩傪巊偆偲椵忔崻偺抣偼偡偖媮傔傜傟傞偺偱丄晛捠偺揹戩傪巊偆偲偄偆
丂丂丂丂敪憐偑崱傑偱偁傑傝側偐偭偨丅懡彮偺斚嶨偝偼偁傞偑丄晛捠偺揹戩偱傕娙扨偵媮傔傜
丂丂丂丂傟傞偙偲偵姶摦偟傑偟偨丅
丂傑偨丄忋婰偺曽朄乮侾乯乣乮俇乯傪堦偮偺悢幃偵傑偲傔傞偲丄暘悢娭悢
丂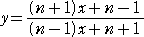
偑摼傜傟傞丅偙偺曽朄傪抦傞偙偲偵傛偭偰丄暘悢娭悢偺帩偮堄枴偑柧椖偵擣幆偝傟傑偟偨丅
偙偺傛偆側婡夛傪梌偊偰偄偨偩偄偨揹戩抝偝傫偵姶幱偄偨偟傑偡丅
丂撉幰偺偨傔偵丄偄偔偮偐楙廗栤戣傪偁偘偰偍偙偆丅
楙廗栤戣丂師偺抣偼丄偍傛偦偄偔傜偲偄偊傞偐丠
乮偙偺傛偆側栤戣傪峫偊傞偙偲偼丄悢揑姶妎傪梴偆偙偲偵懳偟偰桳岠偱偁傞偲怣偠傞丅乯
| 乮侾乯 |
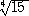 |
乮俀乯 |
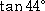 |
乮俁乯 |
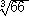 |
乮係乯 |
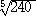 |
乮俆乯 |
 |
| 丂丂 |
|
|
|
|
|
|
|
|
|
| 乮俇乯 |
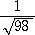 |
|
|
|
|
|
|
|
|
丂奆偝傫偼丄師偺傛偆側宍偱丄埫嶼偺儗儀儖偱媮傔傜傟偨偱偁傠偆偐丠
乮摎乯乮侾乯丂俀亅侾/俁俀亖俇俁/俁俀佮侾丏俋俇俉俈俆丂丂乮幚嵺偺抣偼丄侾丏俋俇俈俋俋丒丒丒乯
乮俀乯丂侾亅兾/俋侽佮侽丏俋俇俆侽俋丂丂乮幚嵺偺抣偼丄侽丏俋俇俆俇俋丒丒丒乯
乮俁乯丂係亄侾/俀係亖俋俈/俀係佮係丏侽係侾俇俈丂丂乮幚嵺偺抣偼丄係丏侽係侾俀係丒丒丒乯
乮係乯丂俁亅侾/侾俁俆亖係侽係/侾俁俆佮俀丏俋俋俀俆俋丂丂乮幚嵺偺抣偼丄俀丏俋俋俀俆俆丒丒丒乯
乮俆乯丂乮偙傟偼丄偪傚偭偲埫嶼偱偼柍棟偐側丠乯
丂丂俁亅侾/侾侽侽侽倢倧倗侾侽佮俀丏俋俋俋俆俈丂丂乮幚嵺偺抣偼丄俀丏俋俋俉俇俋丒丒丒乯
乮俇乯丂乮侾侽亅侾/侾侽乯/俋俉亖俋俋/俋俉侽佮侽丏侾侽侾侽俀丂丂乮幚嵺偺抣偼丄侽丏侾侽侾侽侾丒丒丒乯
丂偲偙傠偱丄俁師曽掱幃丂(倃亅侾)(倃亅俀)(倃亅俁)亖侽丂偺夝偑丄侾 偲 俀
偲 俁 偵側傞偙偲偼丄崅師
曽掱幃傪摿偵妛廗偟偰偄側偔偰傕丄乽壗偲側偔偦偆偩偹両乿偲擺摼偱偒傞帠幚偱偁傠偆丅
丂偦傟偱偼丄俁師曽掱幃丂(倃亅侾)(倃亅俀)(倃亅俁)亖侽丏侽俀丂偺夝偼丄擛壗傎偳偱偁傠偆偐丠
侾 偲 俀 偲 俁 偵嬤偄抣偲梊憐偼偱偒傞偑丄偙偺夝傪尩枾偵媮傔傞偙偲偼擄偟偄丅
丂偟偐偟丄夝偺嬤帡抣偼梕堈偔媮傔傞偙偲偑偱偒傞丅嵍壓恾偐傜暘偐傞傛偆偵丄
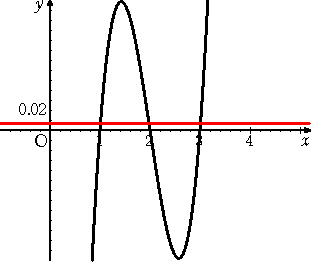 |
丂俥乮倃乯亖(倃亅侾)(倃亅俀)(倃亅俁)亅侽丏侽俀
偲偍偔偲丄曽掱幃丂俥乮倃乯亖侽丂偼丄俁偮偺夝
丂侾亄兛 丄俀亄兝 丄俁亄兞丂傪帩偮丅
丂俥乫乮侾乯亖俀丄俥乫乮俀乯亖亅侾丄俥乫乮俁乯亖俀
丂側偺偱丄丂亅侽丏侽俀亄俀兛 佮侽
丂亅侽丏侽俀亅兝 佮侽
丂亅侽丏侽俀亄俀兞 佮侽
丂傛偭偰丄兛 佮侽丏侽侾丄兝 佮亅侽丏侽俀丄
丂兞 佮侽丏侽侾
丂備偊偵丄俁偮偺夝偺嬤帡抣偼丄
丂丂丂侾丏侽侾丂丄丂侾丏俋俉丂丄丂俁丏侽侾 |
丂捈愙揑偵丄曽掱幃丂(倃亅侾)(倃亅俀)(倃亅俁)亖侽丏侽俀丂傪夝偙偆偲偼巚傢側偄偑丄偙偺傛偆偵
嬤帡抣偱夝傪媮傔傞偲壗屘偐垽傜偟偔姶偠傜傟傞偐傜晄巚媍偩丅
乮捛婰乯丂暯惉俀俉擭俆寧侾俀擔晅偗
丂嬧峴梐嬥偺暋棙寁嶼丄椺偊偽丄尦嬥俙墌傪侾儢寧嬥棙侽丏侽侾亾偱俁儢寧梐偗偨応崌偺尦棙
崌寁俶偼丄俶亖俙乮侾丏侽侽侽侾乯3丂偱梌偊傜傟傞丅侾師嬤帡幃
丂倶佮侽丂偺偲偒丄丂乮侾亄倶乯値佮侾亄値倶
傪梡偄傟偽丄乮侾丏侽侽侽侾乯3佮侾丏侽侽侽俁丂偲偄偆偙偲偼暘偐傞丅
丂倶亖侽 偵偍偗傞儅僋儘乕儕儞揥奐偐傜丄嬤帡幃偑乽侾亄値倶乿偲側傞偙偲偼棟榑揑偵妋偐側偺
偩偑丄偁傑傝偟偭偔傝偟側偄偲偄偆偺偑棪捈側姶憐偱偁傞丅
丂嵟嬤丄偙偺偙偲偺棟夝偵帺慠懳悢偺掙乽倕乿偑娭傢傞偙偲傪抦傞偙偲偑偱偒偨丅
丂倎倶佮侾亄倶丂偲偄偆娭學幃偼丄崱偐傜俁侽侽擭傎偳慜偐傜揤暥傗悢妛偩偗偱側偔宱嵪妶摦偺
敪揥偵偲傕側偄嬥梈娭學偐傜傕丄偦偺廳梫惈偑擣幆偝傟偰偄偨偲偄偆丅偟偐傕偙偺娭學幃傪
枮偨偡倎偼丄僱僀僺傾偺悢 倕 偲尵傢傟傞桞堦偺悢偱偁傞丅
丂師偺傛偆偵寁嶼偡傞偲丄崱傑偱偟偭偔傝偄偐側偐偭偨晹暘偑僗僢僉儕偟偨傛偆側婥暘偩丅
乮侾丏侽侽侽侾乯3亖乮侾亄侽丏侽侽侽侾乯3佮乮倕0.0001乯3亖倕0.0003佮侾亄侽丏侽侽侽俁亖侾丏侽侽侽俁
丂倶傪値攞偡傞偲偄偆寁嶼偼丄寢嬊偺偲偙傠丄巜悢朄懃丂乮倕倶乯値亖倕値倶丂偩偭偨傫偱偡偹両
乮捛婰乯丂乽墌廃棪偺嬤帡寁嶼乿偲戣偟偰丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傜偡偐傞乿偝
丂丂丂傫偐傜偺偛搳峞偱偡丅乮椷榓俀擭俆寧俁擔晅偗乯
丂兾=4(1-1/3+1/5-1/7+乧)丂偼廂懇偑抶偄偙偲偱桳柤偱偡偑丄偆傑偔巊偆偲丄偁傞掱搙偺寘悢
偑媮傔傜傟傑偡丅
丂4(1-1/3+1/5-1/7+乧-1/999999)丂傪寁嶼偡傞偲偒丄
丂晹暘榓 4(1-1/3+1/5-1/7+乧-1/99999)丂偲丂晹暘榓 4(1-1/3+1/5-1/7+乧-1/9999)
傕偲偭偰偍偒傑偡丅偙傟傪俁偮暲傋偰奺寘偺悢帤傪懡悢寛偱寛傔傞偲丄
3丏1413926535917932383626433954795001乧 丂仼 -1/9999傑偱偺榓
3丏1415726535897952384626423832795041乧 丂仼 -1/99999傑偱偺榓
3丏1415906535897932404626433832695028乧 丂仼 -1/999999傑偱偺榓
3丏14159265358979323846264338327950 丂仼 懡悢寛寢壥
偲側傝丄彫悢揰埲壓32寘偑惓偟偔媮傑傝傑偟偨丅
乮僐儊儞僩乯丂懡悢寛偱寛傔傞丄偲偄偆偺偼巃怴側敪憐偱偡偹両偱傕丄乽備傜偓乿偑曗惓偝傟偰
丂丂丂丂丂丂恀偺抣偵嬤偯偔偺偐側丠
乮捛婰乯丂俧俙俬 偝傫偐傜偛搳峞偄偨偩偒傑偟偨丅乮椷榓俇擭俋寧俀係擔晅偗乯
丂俀偮偺柍棟悢偱嬤帡偝偣偰傒傞丅師偺帺慠悢値偼丄俀偮偺柍棟悢傪慻崌偣傞偲丄杦傫偳堦
抳偡傞抣偵嬤偯偗偨丅
n佮 柍棟悢偱偺昞帵丂 仺佮俀悢偺岆嵎偺愨懳抣
3佮 5*sqrt(3)-4*sqrt(2) 仺佮0.0033997883520062724304768106905695204447
8佮 9*sqrt(5)-7*sqrt(3) 仺佮0.00025614451596621299043862804037955033911
12佮 19*sqrt(10)-34*sqrt(2) 仺佮1.4422513975648721560721091917469468432 E-5
14佮 5*sqrt(2)+4*sqrt(3) 仺佮0.00072895785901558188177101292802013936790
16佮 33*sqrt(17)-31*sqrt(15) 仺佮1.9129528747035492978538901538940856089 E-6
18佮 11*sqrt(6)-4*sqrt(5) 仺佮0.00011526061580029453343014683970036989732
20佮 51*sqrt(26)-98*sqrt(6) 仺佮4.0048057270810559023898452505417707900 E-7
24佮 73*sqrt(37)-71*sqrt(35) 仺佮1.1169729827469664119887608509554651446 E-7
28佮 495*sqrt(2)-388*sqrt(3) 仺佮3.7957659268186737979522070518583296012 E-8
32佮 129*sqrt(65)-381*sqrt(7) 仺佮1.4903890174177504572628253724468858932 E-8
36佮 163*sqrt(82)-644*sqrt(5) 仺佮6.5343456440228885554609297031481511666 E-9
40佮 201*sqrt(101)-597*sqrt(11)仺佮3.1252343924574036722748632756462662144 E-9
51佮 15*sqrt(7)+8*sqrt(2) 仺佮2.1835046380752062253901733508985792273 E-5
57佮 21*sqrt(11)-4*sqrt(10) 仺佮9.9567898795034180132923535462276858634 E-6
124佮 29*sqrt(14)+4*sqrt(15) 仺佮2.3987260322773542251636904718057150093 E-6
132佮 105*sqrt(2)-4*sqrt(17) 仺佮1.5467043379248916766181219901488696439 E-6
245佮 47*sqrt(23)+8*sqrt(6) 仺佮4.6203675675934213838670625462524820104 E-7
255佮 159*sqrt(3)-4*sqrt(26) 仺佮3.4908035035075107186334257838554981487 E-7
426佮 69*sqrt(34)+4*sqrt(35) 仺佮1.2327580333941413828310829952623491724 E-7
438佮 75*sqrt(38)-4*sqrt(37) 仺佮1.0148035501276569162826004864350052660 E-7
679佮 95*sqrt(47)+16*sqrt(3) 仺佮4.0798771434653070872845390882949520266 E-8
693佮 101*sqrt(51)-20*sqrt(2) 仺佮3.5365948821905606463899831583875575438 E-8
1016佮 125*sqrt(62)+4*sqrt(63) 仺佮1.5748535453351304854827891931151138080 E-8
1032佮 131*sqrt(66)-4*sqrt(65) 仺佮1.4116608610778294521636201128152863637 E-8
1449佮 159*sqrt(79)+16*sqrt(5) 仺佮6.8247376929139949103118573138778558128 E-9
1467佮 165*sqrt(83)-4*sqrt(82) 仺佮6.2596490147330746056941507128262552391 E-9
1990佮 1379*sqrt(2)+12*sqrt(11) 仺佮3.2371295130920564747781094499907966819 E-9
丂側偍丄
2024佮64778373-1536210*sqrt(1778)(佮2024.0000000077188666499249599539865432)
1825346970佮1881803*sqrt(940902)-4*sqrt(940901)(佮1825346970.0000000000000000000000386764)
側傞柍棟悢偱偐側傝嬤偯偔丅(壓偺悢乽1825346970乿偼0乣9偺悢帤偑堦搙婄傪弌偡僞僀僾偺悢)
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俆擔晅偗乯
丂堦偮偺柍棟悢偱嬤偯偗偰傒傑偟偨丅塃抂偺悢抣偼丄慜俀偮偺嵎偺愨懳抣偱偡丅
堦斒偵丄俉偺攞悢偺帺慠悢偼偄偢傟傕峴偗偦偆偱偡丅
16=42-15*sqrt(3)=>0.019237886466840597088304877411914495791
24=123-70*sqrt(2)=>0.0050506338833465838817893053211345001350
32=276-63*sqrt(15)=>0.0020491889327362337062798137088245173490
40=525-198*sqrt(6)=>0.0010309289307365569377532082335043901511
48=894-143*sqrt(35)=>0.00059101675490591287205430668876207606729
56=1407-780*sqrt(3)=>0.00037009627571104859185362541955378301120
64=2088-765*sqrt(7)=>0.00024703558819826626394846596577432967552
72=2961-1292*sqrt(5)=>0.00017307027171223934761999919110380885978
80=4050-1197*sqrt(11)=>0.00012594458638060942551420518803934464147
88=5379-906*sqrt(30)=>9.4500095344005671898144251386011596633 E-5
96=6972-575*sqrt(143)=>7.2716696137850341565187520446959431717 E-5
104=8853-1350*sqrt(42)=>5.7149388688195943961281204512114323297 E-5
112=11046-783*sqrt(195)=>4.5728919063980887084329367575848946092 E-5
120=13575-899*sqrt(224)=>3.7160906777440839558589688710914293688 E-5
128=16464-1023*sqrt(255)=>3.0607247824951139183948832040071781991 E-5
136=19737-13860*sqrt(2)=>2.5508902623608594282453584631070366255 E-5
144=23418-1295*sqrt(323)=>2.1483200147407576879212274060209928031 E-5
152=27531-8658*sqrt(10)=>1.8262171743553579692301522935038486629 E-5
160=32100-1599*sqrt(399)=>1.5654351913667168657434798770696208115 E-5
168=37149-3526*sqrt(110)=>1.3520456453081349107645400277878002460 E-5
176=42702-1935*sqrt(483)=>1.1757513052464834609167108976471561999 E-5
184=48783-8460*sqrt(33)=>1.0288277537663826978867857967869962110 E-5
192=55416-11515*sqrt(23)=>9.0540344785055006911665795110653250388 E-6
200=62625-9996*sqrt(39)=>8.0096115343544563630858145670082038073 E-6
208=70434-40545*sqrt(3)=>7.1198701339296880836444048825359176973 E-6
216=78867-5830*sqrt(182)=>6.3571982558417182849809728108097647648 E-6
224=87948-9405*sqrt(87)=>5.6996944965601575244751615724698325284 E-6
232=97701-6726*sqrt(210)=>5.1298361531682648788761153900878672073 E-6
240=108150-3599*sqrt(899)=>4.6334908721224596314615983300244219419 E-6
248=119319-30744*sqrt(15)=>4.1991752820486645490899063644723485097 E-6
256=131232-4095*sqrt(1023)=>3.8174932812674583700545221491687345189 E-6
264=143913-34440*sqrt(17)=>3.4807064442220806178631564440052527937 E-6
272=157386-4623*sqrt(1155)=>3.1824025866890528095006338533945508999 E-6
280=171675-29394*sqrt(34)=>2.9172379591251503174251310489710550738 E-6
288=186804-5183*sqrt(1295)=>2.6807351648308626097063006717446215453 E-6
296=202797-32850*sqrt(38)=>2.4691236092811802692280772010616819375 E-6
304=219678-5775*sqrt(1443)=>2.2792126687875382004922224433354285596 E-6
312=237471-24332*sqrt(95)=>2.1082902188077300200429255193613423229 E-6
320=256200-6399*sqrt(1599)=>1.9540409567059134673684620949682723996 E-6
328=275889-26892*sqrt(105)=>1.8144802784198278034278698655600337535 E-6
336=296562-7055*sqrt(1763)=>1.6879004543876111616534704993720122179 E-6
344=318243-14790*sqrt(462)=>1.5728265895810835886254647889304459244 E-6
352=340956-23229*sqrt(215)=>1.4679804112725554698240184211417630657 E-6
360=364725-16198*sqrt(506)=>1.3722503533570500336644416285396892947 E-6
368=389574-25389*sqrt(235)=>1.2846667317585679159772552841492182749 E-6
376=415527-35340*sqrt(138)=>1.2043810565329850268087220171954593041 E-6
384=442608-64505*sqrt(47)=>1.1306487210116121767818178054760610574 E-6
392=470841-192060*sqrt(6)=>1.0628144602296206119864992601618119558 E-6
400=500250-69993*sqrt(51)=>1.0003000900280090029710013420615528427 E-6
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俆擔晅偗乯
丂椺偊偽丄123-70併2 偑 24 偵嬤偄側傜丄115-70併2 偼丄16 偵(42-15併3傛傝傕)嬤偔側傞偲巚
偄傑偡偑丄16 偺偲偒偵丄42-15併3 偲偟偰偄傞偺偼側偤偱偟傚偆偐丅
丂傑偨丄媡偺尒曽偱丄傕偟乽帺慠悢偵嬤偯偗偰偄偔乿偺偑栚揑側傜偽丄塃曈偺帺慠悢傪曄峏偡
傞偙偲偱丄
16佮42-15併3
16佮115-70併2
16佮260-63併15
偺傛偆偵丄嵍曈偺抣傪堦掕偵偟偨傝丄
1佮27-15併3
2佮101-70併2
3佮247-63併15
偺傛偆偵 8 偺攞悢埲奜偵偡傞偙偲傕偱偒傑偡偑丄嵍曈偺抣偑 8 偺攞悢偺傒偲側偭偰偄傞偺
偼丄8 偺攞悢偐傜塃曈傪摫弌偡傞寛傑偭偨庤朄偑偁傞偲偄偆偙偲偱偟傚偆偐丅
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俆擔晅偗乯
丂嵍曈偺抣偑 8 偺攞悢偺傒偲側偭偰偄傞偺偼丄8 偺攞悢偐傜塃曈傪摫弌偡傞寛傑偭偨庤朄
偑偁傞偲偄偆偙偲偱偟傚偆偐丅
丂偁傞杮傪撉傫偱偄偰丄
丂m:=1/2*(sqrt(n+1)+sqrt(n-1))ゥゥゥゥ@
偲抲偔偲偒丄
丂1/m=sqrt(n+1)-sqrt(n-1)ゥゥゥゥゥゥゥ嘇
丂m^2=1/2*(n+sqrt(n^2-1)ゥゥゥゥゥゥゥB
丂n-m^2=1/(4*m^2)ゥゥゥゥゥゥゥゥゥゥゥ嘋
偑惉傝棫偪丄偙傟傜偺摍幃傪慻傒崌傢偣傞偙偲偱丄
1/(8*m^5*(m+sqrt(n))^2)=(m-sqrt(n))^2/(8*m^5*(m^2-n)^2)
=(m^2-2*m*sqrt(n)+n)/(m/2)=2*(m-2*sqrt(n)+n/m)
=(2*n+1)*sqrt(n+1)-(2*n-1)*sqrt(n-1)-4*sqrt(n)ゥゥゥゥゥゥゥ(*)
側傞摍幃偑惉棫偡傞偙偲偵側傞丅嵍曈傪尒傞偙偲偱丄塃曈偺抣偼丄
丂O(1/(n^(5/2)*n)=O(1/n^(3+1/2)偺僆乕僟乕偱傎乁柍帇弌棃傞偙偲偑偱偒傞丅
丂偙偺岻傒側幃傪尒偰丄n+1丄n-1丄n 偑偦傟偧傟暯曽崻併偑奜傟傞奺n偵懳墳偟偰丄
(2*n+1)*sqrt(n+1)佮(2*n-1)*sqrt(n-1)+4*sqrt(n)
(2*n-1)*sqrt(n-1)佮(2*n+1)*sqrt(n+1)-4*sqrt(n)
4*sqrt(n)佮(2*n+1)*sqrt(n+1)-(2*n-1)*sqrt(n-1)
偲偄偆晽偵嵍曈偺帺慠悢傪塃曈偺2偮偺柍棟悢偱峔惉弌棃傞側偲巚偭偰愭掱偺摍幃傕偳偒
傪嶌偭偰偄偒傑偟偨丅
丂側偍丄偙偙偱丄戞俁斣栚偺摍幃傪椉曈暯曽偟偰丄
丂16*n佮8*n^3+10*n-2*(4*n^2-1)*sqrt(n^2-1)
丂亐2偐傜丄
丂8*n佮4*n^3+5*n-(4*n^2-1)*sqrt(n^2-1)ゥ嘍
側傞幃傪棙梡偡傟偽丄8 偺攞悢偺帺慠悢偑塃曈偺堦偮偺柍棟悢偱嬤帡弌棃傞偙偲偑壜擻
偲側傞丅偙偺嘍偐傜峔惉偟偰偄偒傑偟偨丅
丂傜偡偐傞偝傫偺偛巜揈偺條偵丄
gp > forprime(p=2,100,for(n=1,1000000,if(frac(n*sqrt(p)) < 0.000001,print(n";"p))))
978122;3
902702;7
283009;17
566018;17
345777;19
254813;29
509626;29
528641;41
424802;43
829254;47
528896;53
951113;61
977001;89
594030;97
傗
gp > forprime(p=2,100,for(n=1,10000000,if(frac(n*sqrt(p)) > 0.9999999,print(n";"p))))
9369319;2
7865521;3
7465176;5
3096720;7
9504180;11
2298912;17
4508361;19
9016722;19
5412001;23
8193638;29
9600319;31
1311360;41
3697884;43
7395768;43
6191808;47
8142716;61
2874480;71
5748960;71
8623440;71
4684249;73
4121279;79
8242558;79
9005009;89
6377352;97
側傞慺悢傗惍悢傪慻傒崌傢偣傟偽(b偲p傪忋偺慻傒崌傢偣偵庢偭偰偍偔堄枴)丄
丂a+b*sqrt(p)
偼丄a 傪挷愡偡傞偙偲偱堦屄偺柍棟悢偱丄側傫傏偱傕帺慠悢偡傋偰傪岲偒側嬤帡惛搙偱嶌傝
弌偡偙偲偼壜擻偲側傞傫偱偟偨丅
丂偟偐偟丄(*)偺摍幃傪嶌傝弌偣傞僙儞僗偵傎偳傎偳姶怱偟傑偟偨丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俆擔晅偗乯
丂側傞傎偳丄傗偼傝 8 偺攞悢偵偩偗巊偊傞幃偑偁偭偨偺偱偡偹丅傛偔傢偐傝傑偟偨丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俇擔晅偗乯
丂GAI 偝傫偑壗傪偟偨偄偺偐慡偔傢偐傜側偄傫偱偡偑丄16=42-15*sqrt(3) 偑摿暿側嬤帡幃偱
偁傞偐偺傛偆偵埖傢傟偰偄傞棟桼偼偳偙偵偁傞傫偱偡丠
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俇擔晅偗乯
丂16=42-15*sqrt(3) 偑摿暿側嬤帡幃偱偁傞偐偺傛偆偵埖傢傟偰偄傞棟桼偼偳偙偵偁傞傫偱偡丠
丂傜偡偐傞偝傫傊偺曉帠偺拞偺
丂8*n佮4*n^3+5*n-(4*n^2-1)*sqrt(n^2-1)ゥ嘍
側傞幃偐傜丄n=2,7,26 偱惗傑傟傞幃偑埲壓偺幃偲側傞堄枴偱偁傝丄
16=42-15*sqrt(3)
56=1407-780*sqrt(3)
208=70434-40545*sqrt(3)
丂偦偺丂16=42-15*sqrt(3) 偑摿暿側嬤帡幃偲偄偆偮傕傝偼偁傝傑偣傫丅
丂忋偺3偮偺幃偐傜丄
sqrt(3)=(42-16)/15=26/15
sqrt(3)=(1407-56)/780=1351/780
sqrt(3)=(70434-208)/40545=70226/40545
摍偑敪惗偟傑偡丅(慜偵宖帵偟偰偄傞拞偐傜慖傫偱偄傞偩偗偱偡丅)
丂偙偙偵丄sqrt(3) 偺楢暘悢傪搑拞偱懪偪愗偭偰暘悢偲偟偰偄偔庤弴傪帺摦偱傗傜偣偰偄偔偲丄
gp > contfracpnqn(contfrac(sqrt(3)),20)
%208 =
[1 2 5 7 19 26 71 97 265 362 989 1351 3691 5042 13775 18817 51409 70226 191861 262087 716035]
[1 1 3 4 11 15 41 56 153 209 571 780 2131 2911 7953 10864 29681 40545 110771 151316 413403]
偺條偵塃偵峴偔偵偟偨偑偭偰丄傛傝 sqrt(3) 傊嬤帡偟偰偄偗傑偡丅
丂偙偺棳傟偺拞偵丄26/15,1351/780,70226/40545 傕偄傑偡偐傜丄16=42-15*sqrt(3) 偑摿暿
偺幃偲偺夝庍偼丄"偼偰丠"偲巚偭偰偟傑偄傑偡丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俇擔晅偗乯
丂偁偁丄嬶懱揑側曽偑偄偄偐偲巚偭偰1偮拪弌偟偨傜丄幙栤偺堄恾偑揱傢傝傑偣傫偱偟偨丅
丂5斣偺幃偱乽8n=乿偺宍偵偟偨幃偩偗摿暿帇偟偰偄傞偺偼側偤偱偡偐丠
丂偙偺幃傪嶌傞偲偒偵丄偦偺慜偵婰嵹偝傟偨幃傪暯曽偟偰惍棟偟偰摼傜傟傞
丂4*n^3-3*n-(4*n^2-1)*sqrt(n^2-1)佮0
偺椉曈偵撍慠 8n 傪壛偊偰偱偒偨偺偑 5 斣偱偡傛偹丅
丂偙偙偱丄椉曈偵 7n 傪懌偣偽 7 偺攞悢偺幃偑偱偒傞偱偟傚偆偟丄9n 傪懌偣偽 9 偺攞悢偺幃
偑偱偒傞傫偠傖側偄偱偟傚偆偐丠
丂8n 傪慖戰偡傞昁慠惈偼側傫偱偟傚偆丠
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俇擔晅偗乯
丂5斣偺幃偱乽8n=乿偺宍偵偟偨幃偩偗摿暿帇偟偰偄傞偺偼側偤偱偡偐丠
丂偙偺幃傪嶌傞偲偒偵丄偦偺慜偵婰嵹偝傟偨幃傪暯曽偟偰惍棟偟偰摼傜傟傞
丂4*n^3-3*n-(4*n^2-1)*sqrt(n^2-1)佮0
偲婰嵹偝傟偰偄傞晹暘偼丄
丂8*n佮4*n^3+5*n-(4*n^2-1)*sqrt(n^2-1)
傪丄側偤
丂3*n佮4*n^3-(4*n^2-1)*sqrt(n^2-1)
偲偟側偄偺偐丠偲夝庍偟偰偄偄偱偡偐丠
丂棟桼偼丄偙偆偡傞偙偲傪婥晅偐側偐偭偨偱偡丅
丂2偱妱傟傞偐傜偦傟偱廔傢傝偲巚偄崬傒丅偦偺傑傑偱悢抣偱妋擣偵峴偭偰偄傑偟偨丅
丂偙傟偐傜偼丄
6佮32-15*sqrt(3)
9佮108-35*sqrt(8)=108-70*sqrt(2)
12佮256-63*sqrt(15)
ゥゥゥゥゥゥ
偱丄宖嵹偟偰偄偨偙偲偱偟傚偆丅偍慹枛條偱偟偨丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俀俇擔晅偗乯
丂 3*n佮4*n^3-(4*n^2-1)*sqrt(n^2-1)
丂偝傜偵尵偊偽丄3n 偲 4n^3 傪嵍塃偵暘偗傞堄枴傕側偄偲巚偄傑偡丅
丂n 偼嬶懱揑側惍悢傪戙擖偡傞偙偲傪憐掕偟偰偄傞傫偱偟傚偆偐傜丄惍悢偺嬤帡幃偵惍悢傪
懌偡崁偑偁偭偰偼堄媊偑敄偄偱偡丅
丂堦曽偱丄偙傟傪媡偵暯曽崻偺桳棟嬤帡幃偲偟偰丄
丂併(n^2-1) = (4n^3-3n)/(4n^2-1)
偲偟偨幃偼壗偐偵巊偊偦偆偱偡偹丅
乮捛婰乯丂kuiperbelt 偝傫偐傜偛搳峞偄偨偩偒傑偟偨丅乮椷榓俇擭俋寧俁侽擔晅偗乯
丂擇恑懳悢偺嬤帡暘悢偵偮偄偰偱偡丅
丂2傪掙偲偡傞擇恑懳悢 log_{2}(x) 傪 lb(x) 偱昞偡偲丄lb(3)丄lb(5)丄lb(7)丄lb(11)丄lb(13)偺楢暘悢
揥奐偼丄
lb(3)=[1;1,1,2,2,3,1,5,2,23,...]
lb(5)=[2;3,9,2,2,4,6,2,1,1,3,1,18..]
lb(7)=[2;1,4,5,4,5,4,1,29,...]
lb(11)=[3;2,5,1,1,1,25,1,1,...]
lb(13)=[3;1,2,2,1,22,23,1,9,149,...]
偱丄lb(13) 傪 [3;1,2,2,1,22,23,1,9] 偱嬤帡偡傞偲丄
[3;1,2,2,1,22,23,1,9]-lb(13)=201130/54353-lb(13)=-2.25897731584196266637728075571*10^-12
偲側偭偰丄201130/54353 傪 lb(13) 偺嬤帡抣偲偡傞偲丄岆嵎偑彫偝偄偺偱丄lb(3)丄lb(5)丄lb(7)丄
lb(11) 傪 54353攞偡傞偲丄
54353*lb(3)=86147.4668016970019305550728204
54353*lb(5)=126203.757741412805693795471951
54353*lb(7)=152588.162078596956051793358299
54353*lb(11)=188030.486767793017766203979679
偲側偭偰丄彫悢晹暘偵拝栚偡傞偲丄
0.4668016970019305550728204=[0;2,7,33,...]
0.757741412805693795471951=[0;1,3,7,...]
0.162078596956051793358299=[0;6,5,1,...]
0.486767793017766203979679=[0;2,18,2,...]
側偺偱丄偦傟偧傟傪丄1/2=[0;2]丄3/4=[0;1,3]丄1/6={0;6]丄1/2=[0;2] 偱嬤帡偡傞偲丄
(86147+1/2)/54353-lb(3)=6.10790627896702020627740913203*10^-7
(126203+3/4)/54353-lb(5)=-1.42428436437616975547826382828*10^-7
(152588+1/6)/54353-lb(7)=8.44124466103963591405650940218*10^-8
(188030+1/2)/54353-lb(11)=2.43449432087167148461376935139*10^-7
偲側傝傑偟偨丅
丂(86147+1/2)/54353丄(126203+3/4)/54353丄(152588+1/6)/54353丄(188030+1/2)/54353 傪
楢暘悢揥奐偡傞偲丄
(86147+1/2)/54353=[1;1,1,2,2,3,1,5,2,2,1,2,1,12]
(126203+3/4)/54353=[2;3,9,2,2,4,4,1,1,6,1,1,2]
(152588+1/6)/54353=[2;1,4,5,4,5,5,1,4,1,1,2,3]
(188030+1/2)/54353=[3;2,5,1,1,1,25,1,4,1,1,4,2]
傛傝丄
lb(3) 偱丄[1;1,1,2,2,3,1,5,2,...]丄
lb(5) 偱丄[2;3,9,2,2,4,...]丄
lb(7) 偱丄[2;1,4,5,4,5,...]丄
lb(11) 偱丄[3;2,5,1,1,1,25,1,...]
傑偱堦抳偟偰偄偰丄lb(3)丄lb(5)丄lb(7)丄lb(11)丄lb(13) 傪暘曣偑 54353*12=652236 偺暘悢偱丄
斾妑揑傛偔嬤帡偱偒偦偆偱偡丅
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭侾侽寧侾擔晅偗乯
丂lb(3)丄lb(5)丄lb(7)丄lb(11)丄lb(13) 傪捠忢偵楢暘悢偐傜偺懪偪愗傝暘悢偱丄暘曣偑6寘偱偁傞
傕偺傪偲傞偲丄
lb(3)=301994/190537
lb(5)=227268/97879丂(6寘偱偁傞傕偺偼庢傟側偐偭偨丅)
lb(7)=1273419/453601
lb(11)=1444074/417431
lb(13)=201130/54353
偑尒偮偐傞丅
丂kuiperbelt巵偵傛傞峔惉偱偼丄
lb(3)=172295/108706=1033770/652236
lb(5)=504815/217412=1514445/652236
lb(7)=915529/326118=1831058/652236
lb(11)=376061/108706=2256366/652236
lb(13)=201130/54353=2413560/652236
丂偦偙偱丄弶傔偺曽偺堎側傞暘悢傪652236傊偲摑堦偟偨偲偡傟偽丄偦傟偧傟偺暘巕偼丄
lb(3)-->round(652236/190537*301994)=1033770
lb(5)-->round(652236/97879*227268)=1514445
lb(7)-->round(652236/453601*1273419)=1831058
lb(11)-->round(652236/417431*1444074)=2256366
lb(13)-->round(652236/54353*201130)=2413560
偲柕弬側偔偮側偑傝傑偟偨丅
丂丂埲壓丄岺帠拞両



