双対曲線の話題　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「Ｓ（Ｈ）」さんの投稿内容によく「双対曲線」の話題が
出てくる。一説によると、手計算で双対曲線を求めることはほぼ不可能とも言われるが、土
筆の子さんに触発されて、双対曲線の概略や基本的な計算手法についてはまとめてみたい
と最近思うようになった。

　双対曲線を考える対象は射影平面なので、まずは、射影平面の話から始めよう。

　射影直線は直線に無限遠点を追加したものと考えたように、射影平面もアフィン平面に無
限遠直線を追加したものと考えればよい。しかも、アフィン平面内の平行な２直線は無限遠
直線上の１点で交わるという性質をもつ。

　射影平面は、さらに次のような性質をもつ。

（１）　射影平面の均質性：　どの３点も同一直線上にない任意の４点が同様な任意の４点に
　　　　　　　　　　　　　　　　　移す射影変換が存在する

（２）　射影変換により、直線は直線に移り、１直線上の４点の複比は射影変換により不変

（３）　射影平面上の点と直線の双対性


　Ｃを複素数体とし、３次元アフィン空間Ｃ³に対して、Ａ＝Ｃ³−｛（０，０，０）｝とおく。

　Ａ内の２点（ｘ₀，ｘ₁，ｘ₂）、（ｙ₀，ｙ₁，ｙ₂）に対して、同値関係〜を次のように定める。

　　（ｘ₀，ｘ₁，ｘ₂）〜（ｙ₀，ｙ₁，ｙ₂）

　　　⇔　あるλ∈Ｃ−｛０｝があって、　（ｘ₀，ｘ₁，ｘ₂）＝λ（ｙ₀，ｙ₁，ｙ₂）

　同値関係〜による同値類を、代表元（ｘ₀，ｘ₁，ｘ₂）を用いて、（ｘ₀，ｘ₁，ｘ₂）^*で表し、同値
類全体をＰ²＝Ｐ²（Ｃ）と書き、Ｃ上の射影平面という。

　　Ｐ²＝Ａ/〜　・・・　原点を通る直線（原点は除く）全体

　　　　　　

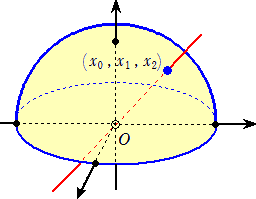
　（ｘ₀，ｘ₁，ｘ₂）^*が、射影平面Ｐ²上の点である。（ｘ₀，ｘ₁，ｘ₂）は、この点の同次座標という。

　射影平面Ｐ²において、　αｘ₀＋βｘ₁＋γｘ₂＝０　（α、β、γ∈Ｃ−｛０｝）
となる点（ｘ₀，ｘ₁，ｘ₂）^*の全体を射影直線という。

例　射影直線では、　Ｌ₀ ： ｘ₀＝０　、Ｌ₁ ： ｘ₁＝０　、Ｌ₂ ： ｘ₂＝０　が基本的である。

　Ｌ₀ は、原点中心、半径１の球面において、

　　　　｛（０，ｘ₁，ｘ₂）｜ｘ₁²＋ｘ₂²＝１、ｘ₁＞０｝∪｛（０，０，１）｝　　（０，０，１）^*：無限遠点

の部分が該当する。Ｌ₁ 、Ｌ₂ も同様である。すなわち、

　　Ｌ₁ ： ｛（ｘ₀，０，ｘ₂）｜ｘ₀²＋ｘ₂²＝１、ｘ₂＞０｝∪｛（１，０，０）｝　　（１，０，０）^*：無限遠点

　　Ｌ₂ ： ｛（ｘ₀，ｘ₁，０）｜ｘ₀²＋ｘ₁²＝１、ｘ₀＞０｝∪｛（０，１，０）｝　　（０，１，０）^*：無限遠点

　これら　Ｌ₀、Ｌ₁ 、Ｌ₂ は、射影平面Ｐ²の座標軸と言われる。

　Ｐ²−Ｌ₀＝｛（１，ｘ₁，ｘ₂）^*｝は、　（１，ｘ₁，ｘ₂）^*　⇔　（ｘ₁，ｘ₂）　により、アフィン平面Ｃ²と
同一視される。その意味で、Ｌ₀は無限遠直線と言われる。

　２つの射影平面　Ｐ₁²、Ｐ₂²において、Ｐ₁²上の直線

　　Ｌ（α，β，γ）： αｘ₀＋βｘ₁＋γｘ₂＝０　 ただし、（α，β，γ）≠（０，０，０）

に対して、Ｐ₂²上の点（α，β，γ）^*を対応させる。また、Ｐ₁²上の点（α’，β’，γ’）^*に対
して、Ｐ₂²上の直線　Ｌ（α’，β’，γ’）：α’ｘ₀＋β’ｘ₁＋γ’ｘ₂＝０　を対応させる。

　この対応をφとするとき、

　（α’，β’，γ’）^*∈Ｌ（α，β，γ）　⇔　αα’＋ββ’＋γγ’＝０

　　　　　　　　　　　　　　　　　　　　　　　 ⇔　（α，β，γ）^*∈Ｌ（α’，β’，γ’）
　すなわち、

　（α’，β’，γ’）^*∈Ｌ（α，β，γ）　⇔　φ（Ｌ（α，β，γ））∈φ（α’，β’，γ’）^*

　このことから、射影平面Ｐ₂²は、射影平面　Ｐ₁²の直線を点とする射影平面と見なすことが
できる。このように対応づけられた２つの射影平面を、双対射影平面という。

　例というのもおこがましいが、高校生のとき、次のような問題に出会った。

　円 ｘ²＋ｙ²＝ｒ² の外部にある点（ａ，ｂ）から円に接線を引くとき、２つの接点を通る
割線の方程式は、ａｘ＋ｂｙ＝ｒ² で与えられることを証明せよ。

（解）　接点（ｘ₁，ｙ₁）、（ｘ₂，ｙ₂）における接線の方程式は、ｘｘ₁＋ｙｙ₁＝ｒ²、ｘｘ₂＋ｙｙ₂＝ｒ²

　　これらが点（ａ，ｂ）を通るので、　ａｘ₁＋ｂｙ₁＝ｒ²、ａｘ₂＋ｂｙ₂＝ｒ²

　　このことは、直線　ａｘ＋ｂｙ＝ｒ²　が２点（ｘ₁，ｙ₁）、（ｘ₂，ｙ₂）を通ることを示す。

　よって、求める割線の方程式は、　ａｘ＋ｂｙ＝ｒ²　　（終）


（コメント）　高校生のとき、上のような解答を示されて、何とも言えない違和感を感じたことを
　　　　　　覚えている。双対を考えると言うことは、上記のような感覚を一般化するものなの
　　　　　　だろうか？


　ｎ次同次多項式　Ｆ（Ｘ₀，Ｙ₁，Ｚ₂）に対して、Ｆ（ｘ₀，ｘ₁，ｘ₂）＝０　のとき、（ｘ₀，ｘ₁，ｘ₂）^*を
Ｆの零点という。Ｆの零点全体の集合　Ｃ＝｛Ｐ∈Ｐ²｜Ｆ（Ｐ）＝０｝を射影平面代数曲線、ま
たは、ｎ次代数曲線という。

　Ｆ（Ｘ₀，Ｙ₁，Ｚ₂）が既約のとき、ｎ次代数曲線は既約と言われる。

　Ｃ上の点Ｐ＝（ｘ₀，ｘ₁，ｘ₂）^*が単純点（通常点）とは、　Ｆ_Ｘ0、Ｆ_X1、Ｆ_X2のうち少なくとも一
つが０でないときをいう。

　Ｆ_Ｘ0、Ｆ_X1、Ｆ_X2の全てが０のとき、特異点という。



　　以下、工事中！