順列・組合せ

順列・組合せの問題に挑戦！　　　　　　　　　　　　　　　　　　　　　

　順列・組合せの問題は、確率論、計算数学、オートマトンの理論および数理経済学において
きわめて重要である。しかし、現行の教育課程においては、深く考えさせる問題が少なく、十
分な訓練ができる状況にはない。ここでは、より進んだ方のために、いくつかの良問を用意し
た。是非、チャレンジしてほしいと思う。

１．　１から１００までの全ての正の整数を同時に印刷するには、何個の活字が必要か？但し、
　　１つの活字には１つの数字のみとする。

２．　さいころを４回振って、出た目の数を順に並べて、４桁の数を作るとき、各位の数字に同
　　じ数字をちょうど３個含む数はいくつできるか？

３．　９１より小さくて、９１と互いに素な自然数は何個あるか？

４．　５個の数字１，２，３，４，５のうちから相異なるもの３個をとって、３桁の正の整数を作る
　　とき、その全ての正の整数の和を求めよ。

５．　４桁の正の整数のうちで、１２３４より大きいものは何個あるか。但し、各位の数字は全て
　　相異なるものとする。

６．　循環節が４個の数字１，３，５，７からできている純循環小数
　　の総和を求めよ。ただし、循環する小数だけからなるものを純
　　循環小数という。

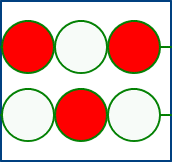
７．　右図のような２本の棒にそれぞれ３個の玉を通したおもちゃ
　　がある。（上下、左右、表裏の区別はしない）
　　この６個の玉を３個は赤く塗り、３個は白く塗るものとすると、
　　何通りの塗り方があるか？

８．　１から１００までの自然数のうちで、各桁に５という数字が少
　　なくとも１つあるものは、いくつあるか。

９．　右図のように、正方形の周上に等間隔に並べられた１２個の　　　
　　点がある。
　　　（１）　少なくとも２点を通る直線の数を求めよ。
　　　（２）　互いに平行でないものは何本あるか。

１０．　１０人の選挙人が５人の候補者を２名連記で無記名投票するとき、票の分かれ方は何
　　通りあるか。但し、選挙人は必ず異なる２名の候補者名を書くものとする。

１１．　７通の手紙とそれに対応した７枚の封筒がある。手紙を封筒に１つずつ入れる時、全て
　　の手紙が対応する封筒に１つも入らない場合の数を求めよ。

１２．　Ａ，Ａ，Ａ，Ｂ，Ｂ，Ｃの７文字から４文字とる順列の数を求めよ。

（答）１．　１９２個　２．　１２０個　３．　７２個　４．　１９９８０　５．　４４７１個　６．　３２／３
　　　７．　６通り　　８．　１９個　　９．（１）　４６本　（２）　１６本　１０．　７０５１通り　
　　１１．　１８５４通り　１２．　３８通り　　（　→　略解へ進む！）

（問題補充）　最近、関西在住の高校生から面白い問題を頂戴しました。順列・組合せの練習
　　　　　　　問題として、良問と判断しましたので、解答を添えての掲載です。

１３．　相異なる形をしたカードが全部で６枚あり、１枚のカードには、アルファベットが１つだけ
　　　記入されている。アルファベットの「Ａ」、「Ｂ」、「Ｃ」が記入されたカードは、それぞれ１枚、
　　　２枚、３枚あるとする。この６枚のカードを一列に並べるとき、次のような並べ方は何通り
　　　あるか。
　　　　　（１）　ＡとＣが隣り合わない並べ方
　　　　　（２）　どのカードも、隣のカードとアルファベットが違う並べ方

　　（１）の（答）：　問題の条件から、６枚のカードは、Ａ、Ｂ１、Ｂ２、Ｃ１、Ｃ２、Ｃ３　としてよい。
　　　　　　　　　　まず、Ｃ１、Ｃ２、Ｃ３の並べ方の数は、３！＝６通り。
　　　　　　　　　　そのうちの１通りに対して、たとえば、Ｃ２　Ｃ３　Ｃ１とする。このＣの並びに
　　　　　　　　　　対して、今度は、Ａの入れ方を考える。可能性として、その入れ方は全部で、
　　　　　　　　　　４通り　ある。
　　　　　　　　　　　各場合について、今度は、Ｂの入れ方を考える。　
　　　　　　　　　　（イ）　Ａ　Ｂ＊　Ｃ２　Ｃ３　Ｃ１　の場合　　（＊は、１，２の何れか）
　　　　　　　　　　　　　この場合は、ＡとＣの間に必ず、Ｂが１個以上入る。
　　　　　　　　　　　　今、上図のように、Ｂが１個入るとして、その選び方は、２通り。
　　　　　　　　　　　　そのうちの１通りに対して、たとえば、
　　　　　　　　　　　　　　　　　　　　　　Ａ　Ｂ２　Ｃ２　Ｃ３　Ｃ１
　　　　　　　　　　　　とする。残りのＢ１の入れ方は、
　　　　　　　　　　　　　　　　　　＾　Ａ　Ｂ２　＾　Ｃ２　＾　Ｃ３　＾　Ｃ１　＾
　　　　　　　　　　　　の、５通りある。したがって、この場合の数は、２×５＝１０通り。
　　　　　　　　　　（ロ）　Ｃ２　Ｃ３　Ｃ１　Ｂ＊　Ａ　の場合　　（＊は、１，２の何れか）
　　　　　　　　　　　　　この場合は、上の場合と同様にして、２×５＝１０通り。
　　　　　　　　　　（ハ）　Ｃ２　Ｂ＊　Ａ　Ｂ＊　Ｃ３　Ｃ１　　（＊は、１，２の何れか）
　　　　　　　　　　　　　この場合は、Ａの左右は必ずＢとなる。Ｂの入れ方は、２！＝２通り。
　　　　　　　　　　（ニ）　Ｃ２　Ｃ３　Ｂ＊　Ａ　Ｂ＊　Ｃ１　　　（＊は、１，２の何れか）
　　　　　　　　　　　　　この場合は、上の場合と同様にして、２！＝２通り。
　　　　　　　　　　以上から、求める場合の数は、
　　　　　　　　　　　　　　　　　　３！×（１０＋１０＋２＋２）＝１４４通り

　　（２）の（答）：　まず、Ｃ１、Ｃ２、Ｃ３の並べ方の数は、３！＝６通り。
　　　　　　　　　　そのうちの１通りに対して、たとえば、Ｃ２　Ｃ３　Ｃ１とする。このＣの並び
　　　　　　　　　　に対して、今度はＡとＢの入れ方を考える。可能性として、次のように入
　　　　　　　　　　れる場合（イ）～（ニ）があります。
　　　　　　　　　　（イ）　◎　Ｃ２　◎　Ｃ３　◎　Ｃ１　（◎は、ＡまたはＢ）
　　　　　　　　　　　　　この場合、◎にＡとＢを並べる方法の数は、３！＝６通り。
　　　　　　　　　　（ロ）　　　Ｃ２　◎　Ｃ３　◎　Ｃ１　◎　　（◎は、ＡまたはＢ）
　　　　　　　　　　　　　この場合、◎にＡとＢを並べる方法の数は、３！＝６通り。
　　　　　　　　　　（ハ）　　　Ｃ２　◎◎　Ｃ３　◎　Ｃ１（◎◎は必ず、ＡとＢのペア！）
　　　　　　　　　　　　　この場合、まず、Ａは考えないで、Ｂ２個を並べる。その方法の数は、
　　　　　　　　　　　　　２！＝２通り。そのうちの１通り、たとえば、
　　　　　　　　　　　　　　　　Ｃ２　Ｂ２　Ｃ３　Ｂ１　Ｃ１
　　　　　　　　　　　　　とする。Ａは、Ｂ２の左または右に入ることになる。
　　　　　　　　　　　　　　　　Ｃ２　○　Ｂ２　○　Ｃ３　Ｂ１　Ｃ１
　　　　　　　　　　　　　その場合の数は、２通りとなる。
　　　　　　　　　　　　　　よって、この場合の並べ方の数は、２！×２＝４通り。　　　　　　　　
　　　　　　　　　　（ニ）　　　Ｃ２　◎　Ｃ３　◎◎　Ｃ１（◎◎は必ず、ＡとＢのペア！）
　　　　　　　　　　　　　この場合、上の場合と同様にして、２！×２＝４通り。
　　　　　　　　　　　以上から、求める場合の数は、
　　　　　　　　　　　　　　　　　　　３！×（３！＋３！＋２！×２＋２！×２）＝１２０通り

（追記）　最近、冒頭の問題１．～１２．を解かれた方から解答の誤りがある旨、ご教示いた
　　　　　だいた。今から、２年９ヶ月前ほどにアップロードしたものだが、その間、解答が誤っ
　　　　　たままだったわけで、大変申し訳なく思う。（上記の解答は、訂正済み！）

　　　　　　私自身の確認の意味も込めて、略解を提示することとした。この略解が読者の学
　　　　　習の一助になれば幸いである。

１．　９＋２×１０×９＋３＝１９２（個）

２．　６×５×４！/３！＝１２０（個）

３．　９１＝７×１３　なので、９１と公約数を持つものは、６＋１２＋１＝１９（個）
　　　したがって、９１と互いに素な自然数は、９１－１９＝７２（個）

４．　（１＋２＋３＋４＋５）×１１１×₄Ｐ₂＝１９９８０

５．　１２３４より小さいものは、　１＋７＋₈Ｐ₂＝６４（個）　なので、
　　　求める個数は、　９×₉Ｐ₃－１－６４＝４４７１（個）

６．　循環小数を　ｘ　とおくと、　９９９９・ｘ＝（１、３、５、７　を並べた整数）　なので、
　　求める総和は、　（１＋３＋５＋７）×１１１１×３！÷９９９９＝３２/３

７．　上段が全て赤の場合は、１通り。上段が赤２個の場合、下段のパターンは、５通り。
　　よって、求める場合の数は、　１＋５＝６（通り）

８．　５が各桁に全く含まれない自然数は、　８＋８×９＋１＝８１（個）あるので、
　　求める場合の数は、　１００－８１＝１９（個）

９．（１）　₁₂Ｃ₂－₄Ｃ₂×４＋４＝４６（本）

　　（２）　傾きに注目して、０、±１/３、±１/２、±２/３、±１、±３/２、±２、±３、∞　の
　　　　　１６（本）

１０．　Ａ＋Ｂ＋Ｃ＋Ｄ＋Ｅ＝２０　（０≦　Ａ、Ｂ、Ｃ、Ｄ、Ｅ　≦１０）　となる解の組の個数を
　　　求めればよい。
　　　　そのためには、Ａ＋Ｂ＋Ｃ＋Ｄ＋Ｅ＝２０　（０≦　Ａ、Ｂ、Ｃ、Ｄ、Ｅ　≦２０）　となる
　　　解の組の個数から、Ａ、Ｂ、Ｃ、Ｄ、Ｅ　が１１以上となる場合の数を求めればよい。
　　　　Ａが１１以上のとき、まずＡに１１を留保し、残りの９をＡ、Ｂ、Ｃ、Ｄ、Ｅ　に分ければ
　　　よい。その場合の数は、₅Ｈ₉＝₁₃Ｃ₉＝₁₃Ｃ₄＝７１５（通り）
　　　　Ｂ、Ｃ、Ｄ、Ｅ　が１１以上となる場合の数も同様で、これらは全て重複しない。
　　　　したがって、求める場合の数は、
　　　　　　　₅Ｈ₂₀－７１５×５＝１０６２６－３５７５＝７０５１（通り）

１１．　ｎ通の手紙がｎ枚のそれぞれが対応する封筒に１つも入らない場合の数をＦ(ｎ)
　　　とおくと、Ｆ(１)＝０、Ｆ(２)＝１、ｎが３以上のとき　Ｆ(ｎ)＝(ｎ－１)(Ｆ(ｎ－２)＋Ｆ(ｎ－１))
　　　が成り立つ。このとき、Ｆ(３)＝２、Ｆ(４)＝９、Ｆ(５)＝４４、Ｆ(６)＝２６５　より、
　　　Ｆ(７)＝１８５４　となり、求める場合の数は、１８５４通りである。

１２．　ＡＡＡＢの並べ方は、４通り、ＡＡＡＣの並べ方は、４通り、ＡＡＢＢの並べ方は、６通り、
　　　ＡＡＢＣの並べ方は、１２通り、ＡＢＢＣの並べ方は、１２通り。
　　　　よって、求める場合の数は、　４＋４＋６＋１２＋１２＝３８（通り）

（問題補充２）　順列・組合せの問題として、興味ある解法に出会ったので紹介したい。

１４．　凸ｎ角形の頂点を頂点とし、対角線を辺とする三角形は、全部で何個あるか？

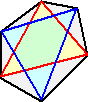　　　左図のような凸６角形には、問題の条件を満たす三角形は、２個しか
　　ない。

　　　ｎの値が小さければ数える気力も起こるが、一般のｎなので、途方に
　　暮れてしまう人がいるかもしれない。

　高校では、このような問題は次のように解かれるのが普通だろう。

　ｎ個の頂点から３個の頂点を選ぶ場合の数は、_ｎＣ₃ ＝ｎ（ｎ－１)(ｎ－２）/６（個）
このうち、凸ｎ角形と１辺を共有するものは、ｎ（ｎ－４）（個）
　　　　　　凸ｎ角形と２辺を共有するものは、ｎ（個）
したがって、求める場合の数は、
　　　　　　ｎ（ｎ－１)(ｎ－２）/６－ｎ（ｎ－４）－ｎ＝ｎ（ｎ－４)(ｎ－５）/６（個）
である。

（コメント：　（ｎ－４)(ｎ－５）/６＝_ｎ－4Ｃ₂/３　であることを考えると、別解の存在に気づかさ
　　　　　　れる。）

　上記では、三角形の個数なので、比較的容易であったが、もし、凸四角形とか一般の凸
ｍ角形の個数となると、俄然難しくなる。

　しかし、このような一見難しそうな場合についても、実は、有効な計算方法がある。

一般に、

凸ｎ角形の頂点を頂点とし、対角線を辺とする凸ｍ角形は、全部で何個あるか？

という問題は、ケリーの問題といわれる。
　　　　　　　　（Ａｒｔｈｕｒ　Ｃａｙｌｅｙ　1821～1895 英国）

　まず、問題の条件を満たすような凸ｍ角形が存在するためには、凸６角形の場合から

も分かるように、
　　　　　　　　　　　　　　　　ｎ ≧ ２ｍ
でなければならない。

　いま、凸ｎ角形のｎ個の頂点を、　１、２、３、・・・、ｎ　と番号で明示する。

　そこで、凸ｎ角形の頂点のうち、たとえば、ｎ－１が、凸ｍ角形の１つの頂点になって

いる場合を考える。

　残りのｍ－１個の頂点を番号の若い順に、ｋ₁、ｋ₂、・・・、ｋ_ｍ－1　とおく。

　このとき、　１ ≦ ｋ₁ ＜ｋ₂ ＜　・・・　＜ｋ_ｍ－1 ≦ ｎ－３　であるが、

ｋ₁、ｋ₂、・・・、ｋ_ｍ－1 は、さらに次の条件を満たさなければならない。

　　ｋ₁ ＋１＜ｋ₂

　　ｋ₂ ＋１＜ｋ₃　より、　ｋ₁ ＋２＜ｋ₃　　　よって、　ｋ₁ ＜ｋ₃－２

　　ｋ₃ ＋１＜ｋ₄　より、　ｋ₁ ＋３＜ｋ₄　　　よって、　ｋ₁ ＜ｋ₄－３

　　　・・・・・・・・・・

　　ｋ_ｍ－2 ＋１＜ｋ_ｍ－1 より、　ｋ₁ ＋ｍ－２＜ｋ_ｍ－1　　　よって、　ｋ₁ ＜ｋ_ｍ－1－ｍ＋２

　よって、

　１ ≦ ｋ₁ ＜ｋ₂－１＜ｋ₃－２＜　　・・・　＜ｋ_ｍ－1－ｍ＋２ ≦ ｎ－３－ｍ＋２

となるように、ｋ₁、ｋ₂、・・・、ｋ_ｍ－1 を選べばよい。

このとき、条件を満たすようなｋ₁、ｋ₂、・・・、ｋ_ｍ－1 の選び方は、

　１からｎ－ｍ－１（＝ｎ－３－ｍ＋２）までの自然数から、異なるｍ－１個の自然
数を選ぶ場合の数に等しい

ので、凸ｎ角形の頂点ｎ－１が、凸ｍ角形の１つの頂点になっているような場合の数は、

　　　　　　　　　　　　　_{ｎ－ｍ－1}Ｃ_ｍ－1

で与えられる。このことを、凸ｎ角形のすべての頂点で考えると、ｍ個ずつ重複して数え

ているので、求める場合の数は、

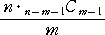　（個）

となる。

　実際に、ｍ＝３の場合に公式を適用すると、　ｎ・_ｎ－4Ｃ₂/３　となって当初の示唆に一致
することが確かめられた。

（問題補充３）　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんが、当ＨＰの掲示板「出会
　　　　　　　　　いの泉」に『微妙な違い』と題して次のような問題を出題された。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２２年３月２８日付け）

　ちょっとした条件の違いで考え方が異なってくる感覚を鍛えていただければ幸いである。
このような問題を整理していただいたＧＡＩさんに感謝します。

【問題群】

（１）相異なる３個の球を、相異なる７個の箱に自由に配る（空き箱を許す）方法は何通り？

　　（解）　重複順列。　７×７×７＝７³　（通り）

（２）相異なる３個の球を、相異なる７個の箱に高々１個配る方法は何通り？

　　（解）　順列。　₇Ｐ₃　（通り）

（３）相異なる７個の球を、相異なる３個の箱に少なくとも１個配る方法は何通り？

　　（解）　重複順列の応用。　３⁷－₃Ｃ₁（２⁷－２）－₃Ｃ₂＝３⁷－３・２⁷＋３　（通り）

（４）区別できない３個の球を、相異なる７個の箱に自由に配る方法は何通り？

　　（解）　重複組合せ。　₇Ｈ₃　（通り）

（５）区別できない３個の球を、相異なる７個の箱に高々１個配る配り方は何通り？

　　（解）　組合せ。　₇Ｃ₃　（通り）

（６）区別できない７個の球を、相異なる３個の箱に少なくとも１個配る配り方は何通り？

　　（解）　重複組合せの応用。　₃Ｈ₄　（通り）

（７）相異なる３個の球を、区別できない７個の箱に自由に配る配り方は何通り？

　　（解）　３個、２個１個、１個１個１個より、　１＋₃Ｃ₂＋１＝５　（通り）

（８）相異なる３個の球を、区別できない７個の箱に高々１個配る配り方は何通り？

　　（解）　明らかに、１通りしかない。

（９）相異なる７個の球を、区別できない３個の箱に少なくとも１個配る配り方は何通り？

　　（解）　重複順列の応用。　（３⁷－３・２⁷＋３）/３！　（通り）

（１０）区別できない３個の球を、区別できない７個の箱に自由に配る方法は何通り？

　　（解）　３＝２＋１＝１＋１＋１　の３通り。

（１１）区別できない３個の球を、区別できない７個の箱に高々１個配る配り方は何通り？

　　（解）　明らかに、１通りしかない。

（１２）区別できない７個の球を、区別できない３個の箱に少なくとも１個配る配り方は何通り？

　　（解）　４＝３＋１＝２＋２＝２＋１＋１　の４通り。

（コメント）　答えは合っているかな？

（問題補充４）　順列・組合せの問題は、答えを見るまで安心できない危うさがまた一つの魅
　　　　　　　　力でもある。答えが合っているときの嬉しさと言ったら半端ない。普通の演習問
　　　　　　　　題としては、それほど意識しないが、受験時の問題に順列・組合せの問題を見
　　　　　　　　るとイヤ～な雰囲気が漂い出す。（平成２６年５月２５日付け）

　次は、東北大学後期理系（２０１４）の問題である。

　縦横の長さの比が１：３の長方形の板がある。この板を両面とも下図のように線で区切り、
できた６つの正方形のそれぞれに赤または白の色を塗ることにする。塗り終えた板におい
て回転や裏返しで同じ塗り方になるものは区別しないとするとき、塗り方は何通りあるか求
めよ。ただし、各正方形には１つの色を塗るものとする。

　　　　　　　　　（表面）　　　　　　　　　　　　　　　（裏面）
　　　　　　　　　　

（解）　表面左から、１２３、裏面左から、４５６として、１２３４５６の順列を考える。

・６ヶ所すべて同じ色のとき、　赤赤赤赤赤赤、白白白白白白　の２通り

・５ヶ所のみ同じ色のとき、

　　赤赤赤赤赤白、赤赤赤赤白赤、白白白白白赤、白白白白白赤白　の４通り

・４ヶ所のみ同じ色のとき、

　　赤赤赤赤白白、赤赤赤白赤白、赤赤白赤赤白、
　　赤白赤赤赤白、白赤赤赤赤白、赤白赤赤白赤、
　　白白白白赤赤、白白白赤白赤、白白赤白白赤、
　　白赤白白白赤、赤白白白白赤、白赤白白赤白　の１２通り

・３ヶ所のみ同じ色のとき、

　　赤赤赤白白白、赤赤白赤白白、赤白赤赤白白、
　　白赤赤赤白白、赤赤白白赤白、赤白赤白赤白　の６通り

　　　以上から、　２＋４＋１２＋６＝２４通り

（問題補充５）　順列・組合せの問題で、次のような問題がある。（平成２７年２月１５日付け）

　Ｓ、Ｕ、Ｇ、Ａ、Ｋ、Ｕの６文字を一列に並べるとき、Ｓ、Ｇ、Ｋがこの順にあるものは何通り
あるか。

　この問題に対して、次の解はよく知られたものだろう。

（解）　Ｓ、Ｇ、Ｋの３文字を同じ文字○とみなして、○、Ｕ、○、Ａ、○、Ｕの順列を考えればよ
　　　いので、
　　　　　　　　　６！/（３！２！）＝６０（通り）　　（終）

　これに対して、次のような別解があることを最近知ることが出来た。

（別解）　１、２、３、４、５、６　の６個の番号からＳ、Ｇ、Ｋの３つを入れる番号を選ぶとき、
　　　　　₆Ｃ₃＝２０（通り）　このうちの１通りに対して、残りのＵ、Ａ、Ｕの並べ方は、
　　　　　３！/２！＝３（通り）
　　　　よって、求める場合の数は、　２０×３＝６０（通り）　　（終）