円のある性質２　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　同じ長さをもつ、すべての閉じたなめらかな曲線の中で最大の面積を囲むものが「円周」
であることはよく知られた事実である。素朴な図形である円であるが、このほかにもいろい
ろな性質を秘めている。

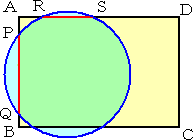例えば、ただ漠然と長方形と円を交わらせても、特徴 　　ある性質は浮かび上がってこないが、意図的に、円が 　　長方形を切り取る弦（赤色の部分）の長さが等しい場合 　　に注目してみると、ある性質の成り立つことが分かる。

右図において、　ＰＱ＝ＲＳ　が成り立つとき、 　　　　　　ＡＰ ＝ ＡＲ が成り立つ。

　証明は易しい。

（証明）　方べきの定理より、　ＡＰ・ＡＱ＝ＡＲ・ＡＳ　なので、ＰＱ＝ＲＳ＝Ｋ　とおくと、

　　　　　　　　ＡＰ・（ＡＰ＋Ｋ）＝ＡＲ・（ＡＲ＋Ｋ）

　　　　ＡＰ²＋ＡＰ・Ｋ＝ＡＲ²＋ＡＲ・Ｋ　　より、　（ＡＰ−ＡＲ）（ＡＰ＋ＡＱ＋Ｋ）＝０

　　　　ＡＰ＋ＡＱ＋Ｋ≠０　なので、　ＡＰ−ＡＲ＝０　すなわち、　ＡＰ＝ＡＱ　（証終）


　証明からも分かるように、この性質は長方形という性質に依らない。すなわち、一般の四
辺形において成り立つ性質である。すなわち、次の事実が成り立つ。

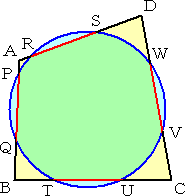左図のように、四辺形ＡＢＣＤに円が交わっている。 　　　ただし、４つの弦ＰＱ、ＴＵ、ＶＷ、ＲＳの長さは全て等 　　　しいものとする。 　　　　このとき、　　ＡＢ＋ＣＤ＝ＢＣ＋ＤＡ 　　　が成り立つ。

　証明は、明らかであろう。


（追記）　令和４年１月１０日付け

　円の中心を求める方法は、２つの弦の垂直２等分線の交点など、いくつか知られている。

　　　

　手っ取り早い方法として、次の方法はどうだろうか。

　円に２つの角で内接する長方形を考える。

　　

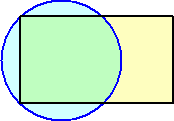
　このとき、円の中心は、２本の赤線の交点として求められる。

　　

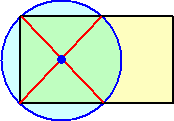
　証明は、赤線が円の直径であることから明らかだろう。