円のある性質　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　新学習指導要領では、円の性質の面白い部分がほとんど中学３年から高校１年に移行
してしまった。

　今回は、中学の数学の範囲で成り立つことが示される、次の面白い性質を紹介したい。

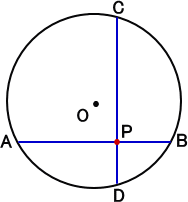左図のような半径 Ｒ の円がある。 　　　円内の任意の点Ｐにおいて、直交する２直線を引き、 　　　円周との交点をそれぞれ、Ａ、Ｂ、Ｃ、Ｄ　とする。 　　　　このとき、次の等式が成り立つ。 　　　ＰＡ2＋ＰＢ2＋ＰＣ2＋ＰＤ2＝（２Ｒ）2

　証明は、次のようなものが知られている。

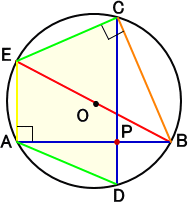ＣＤに平行に、線分ＡＥを引く。このとき、∠ＢＡＥ＝９０° 　　なので、線分ＢＥは直径となる。よって、∠ＢＣＥ＝９０° 　　また、ＣＤ、ＡＥは、円の平行な弦なので、四角形ＡＤＣＥ 　　は、等脚台形で、ＡＤ＝ＣＥ　が成り立つ。 　　従って、　　ＰＡ2＋ＰＢ2＋ＰＣ2＋ＰＤ2 　　　　　　　＝（ＰＡ2＋ＰＤ2）＋（ＰＢ2＋ＰＣ2） 　　　　　　　＝ＡＤ2＋ＢＣ2 　　　　　　　＝ＣＥ2＋ＢＣ2 　　　　　　　＝ＢＥ2 　　　　　　　＝（２Ｒ）2 　　となり、等式は成り立つ。

（参考文献 ： ピーター・フランクル　著　数学問題集　１　（日本評論社））