円に内接する四角形　 　　 　　　　　　　　　　　　　　　　　　　　　

正三角形は円に内接し、正三角形の重心は外接円の中心（外心） 　　となるという性質は有名だろう。 　　　このページで注目する事象は、この素朴な性質を出発点とする。

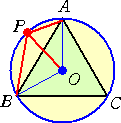左図において、　∠ＡＯＰ＝θ　とおくと、　∠ＢＯＰ＝２π/３−θ 　　このとき、　∠ＡＰＢ＝π−θ/２−（π/３−θ/２）＝２π/３ 　　これは、円に内接する四角形の性質からも明らかだろう。

　θの値に関わらず、∠ＡＰＢが一定という自然な性質が示された。

　このような点Ｐを、弧ＢＣ上、弧ＣＡ上にとると、面白い性質がクローズアップされる。

　

　上図において、　∠ＡＯＰ＝∠ＢＯＱ＝∠ＣＯＲ＝θ　とおくと、

　　　∠ＰＡＲ＝π/３＋θ/２＋（π/３−θ/２）＝２π/３

同様にして、　∠ＰＢＱ＝２π/３　、　∠ＱＣＲ＝２π/３

　以上から、６角形ＡＰＢＱＣＲの６個の頂角はすべて等しい。

　ここで、θ＝π/３　ならば、６角形ＡＰＢＱＣＲは正６角形となるが、θ≠π/３　のときは、

正６角形とは言えない。

　上記の構成法を考えると、一般に次の事実が成り立つことは明らかだろう。

　頂角がすべて等しく、円に内接する２ｎ角形の中には正２ｎ角形にならないものが
存在する

　ところが、これに対して次の驚くべき事実が知られている。

　頂角がすべて等しく、円に内接する２ｎ＋１角形は、必ず正２ｎ＋１角形になる

　偶数と奇数。この差はどこから来るのだろう？

　偶数の場合は、

　

からも分かるように、△ＯＡＰ、△ＯＰＢ、、△ＯＢＱ、△ＯＱＣ、△ＯＣＲ、△ＯＲＡ　と合同な
三角形が一つおきに出現し、△ＯＡＰと△ＯＲＡが合同になることは、θ＝π/３　のときを
除き、起こり得ない。

　それに対して、奇数のときは、合同な三角形が一つおきに出現し、必然的にすべての三
角形が合同にならざるを得ない状況になる。これが、偶数の場合と奇数の場合の状況の
差である。

　頂角がすべて等しい、円に内接する５角形の場合を見てみよう。

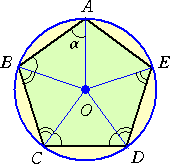左図において、頂角の大きさをθとすると、 　　　　　∠ＯＢＣ＝θ−α 　　で、∠ＯＥＤ＝θ−α　から、　∠ＯＡＥ＝∠ＯＥＡ＝α 　　このとき、頂角Ａにおいて、　α＋α＝θ　から、　α＝θ/２ 　　　よって、　∠ＯＢＣ＝θ/２

したがって、２等辺三角形ＯＡＢ、ＯＢＣ、ＯＣＤ、ＯＤＥ、ＯＥＡはすべて合同となる。

　このとき、　ＡＢ＝ＢＣ＝ＣＤ＝ＤＥ＝ＥＡ　より、５角形ＡＢＣＤＥは正５角形となる。

　上記の議論を、「頂角がすべて等しく、円に内接する２ｎ＋１角形」に拡張するのは容易だ
ろう。

　辺の数が奇数の場合は、隣り合う三角形同士が合同となり、結果として、辺の長さがすべ
て等しくなり、「正２ｎ＋１角形」にならざるを得なくなる。これが辺の数が偶数の場合との決
定的な違いである。


（追記）　令和６年１２月１４日付け

　次の東北大学　理系（１９８８）の問題は、円に内接する四角形の性質も使えて、奥が深い
問題でした。

問題１　　平面上に点Ｏを中心とする半径５の円がある。その周上に４点Ａ、Ｂ、Ｃ、Ｄがこの
　　順序にあり、ＯＡ＝−ＯＤが成り立つ。線分ＡＣとＢＤの交点をＰとし、∠ＡＰＢ＝θとする。
　　線分ＡＢとＤＣの長さをそれぞれ４、５として、次の値を求めよ。

　

（１）　内積ＯＡ・ＡＢ
（２）　ｃｏｓθ
（３）　内積ＡＢ・ＤＣ

（解）（１）　ＯＡ・ＡＢ＝ＯＡ・（ＯＢ−ＯＡ）＝ＯＡ・ＯＢ−ＯＡ²

　　＝（ＯＡ²＋ＯＢ²−ＡＢ²）/２−２５＝（２５＋２５−１６）/２−２５＝−８

（２）　∠ＯＡＢ＝α　とおくと、（１）より、　５・４・ｃｏｓ（π−α）＝−８　なので、ｃｏｓα＝２/５

このとき、　ｓｉｎα＝（√２１）/５　である。△ＯＣＤは正三角形なので、∠ＯＡＢ＝２π/３−θ

すなわち、　θ＝２π/３−α　となり、

ｃｏｓθ＝ｃｏｓ（２π/３−α）＝（−１/２）ｃｏｓα＋（/２）ｓｉｎα＝−１/５＋（３/１０）

よって、　ｃｏｓθ＝（３−２）/１０

（３）　ＡＢ・ＤＣ＝４・５・ｃｏｓθ＝２（３−２）　　（終）



　　　以下、工事中