円と接線　　　 　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　

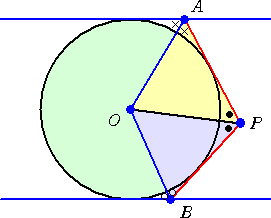
　次の場面設定の場合、　ＰＡ・ＰＢ＝ＯＰ²　が成り立つことは明らかである。

　　　　　　　　

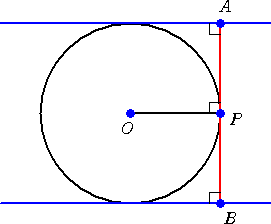
　実は、次の図においても、　ＰＡ・ＰＢ＝ＯＰ²　が成り立つ。

　　　　　　　　

　実際に、

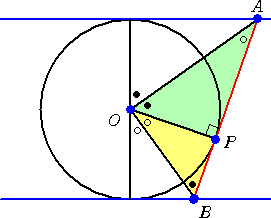
　　　　左図において、

　　　　　　△ＡＯＰ∽△ＯＢＰ　なので、

　　　　　　　ＰＡ ： ＯＰ ＝ ＯＰ ： ＰＢ

　　　　よって、

　　　　　　　　　ＰＡ・ＰＢ＝ＯＰ²

　　　　が成り立つ。


　この問題は次のような場面設定の問題に拡張される。


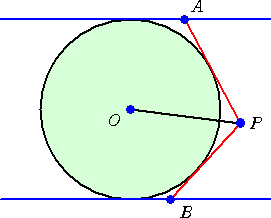
　　　円Ｏの外部の点Ｐより接線を引き、円Ｏの

　　平行な２接線との交点をそれぞれＡ、Ｂとおく。

　　　このとき、

　　　　　　　　　ＰＡ・ＰＢ＝ＯＰ²

　　　　が成り立つ。




　このことを示す場合、やはり相似三角形の利用に気がつくことが解決の第一歩だろう。

左図において、 　　　　　∠ＯＡＰ＋∠ＯＰＡ＋∠ＯＢＰ＝１８０° 　　が成り立つので、 　　　∠ＯＡＰ＝∠ＢＯＰ　　、　∠ＡＯＰ＝∠ＯＢＰ 　　である。（三角形の内角の和は１８０°！） 　　　よって、　△ＡＯＰ∽△ＯＢＰ　なので、 　　　　　　　ＰＡ ： ＯＰ ＝ ＯＰ ： ＰＢ 　　より、　ＰＡ・ＰＢ＝ＯＰ2　　が成り立つ。

　　以下、工事中