立体角　　　　 　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　弧度法では、半径１の円に対して、弧の長さ１の弧を見込む角が、１ラジアンであった。こ
のことは、換言すれば、原点から出る２直線のなす角が、２直線が切り取る円弧の長さで定
義されることに等しい。

　この考え方を自然に拡張すれば、立体角の概念が生まれる。すなわち、三次元空間にお
ける「ある点からの広がりの大きさ」を表す量（立体角）を、半径１の球で切り取られる球
面上の図形の面積で定義することは自然な拡張だろう。

　半径１の球で切り取られる球面上の図形の面積は、0 以上4π以下で、立体角の単位は、
ステラジアン（steradian、sr）が用いられる。


例　直方体の頂点における立体角を求めてみよう。

　半径１の球面の表面積の１/８なので、４π・（１/８）＝π/２

　何となく直角っぽくイメージされるのかな？


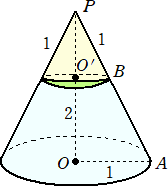
例　底面の半径が１で高さが２の直円錐の立体角を求めてみよう。

円錐の中心軸と母線がなす角度をαとおくと、 　　　ｃｏｓα＝２/である。 　円錐の中心軸から測った角度をθ（０≦θ≦α）とすると、 　半径１の球で切り取られる球面上の図形の面積は、

　よって、上記の円錐の頂点における立体角は、

　　　（１０−４）π/５　（ステラジアン）

であると言える。

　もっとも円錐の場合は、円錐の中心軸と母線のなす角度で広がり具合を表した方がわか
りやすいかも．．．。