ホルディッチの定理　　　　　　　　　　　　　　　　　　　　　　　　　　

　最近、不思議おもしろ幾何学事典（Ｄ．ウェルズ　著　宮崎興二　他訳　（朝倉書店））を何
とはなしに眺めていたら、「ホルディッチの定理」なるものがあることを知った。

ホルディッチの定理（Holditch's Theorem）　・・・　Ｈｏｌｄｉｔｃｈ（１８５８）

　平面上の滑らかな凸閉曲線Ｃにおいて、ある一定の長さ（＝ｐ＋ｑ）の弦を、その両

端点が曲線Ｃ上にくるようにすべらして動かすとき、弦の長さをｐとｑに分ける点は新

しい閉曲線Ｃ’を描く。

　このとき、２つの閉曲線ＣとＣ’で囲まれる部分の面積は、πｐｑ で与えられる。

例　原点中心で半径が ２ｒ の円Ｃ ： ｘ²＋ｙ²＝４ｒ² において、長さ ２ｒ の弦を考える。弦の
　　中点Ｍの軌跡Ｃ’の方程式を求めてみよう。

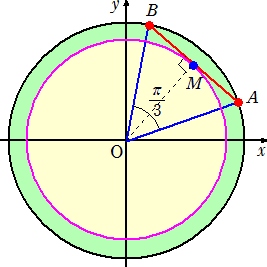左図において、　Ａ（２ｒ・ｃｏｓθ，２ｒ・ｓｉｎθ） 　　Ｂ（２ｒ・ｃｏｓ（θ＋π/３），２ｒ・ｓｉｎ（θ＋π/３）） 　とおくと、弦の中点Ｍ（ｘ，ｙ）の座標は、 　　ｘ＝（２ｒ・ｃｏｓθ＋２ｒ・ｃｏｓ（θ＋π/３））/２ 　　 ＝ｒ・ｃｏｓ（θ＋π/６） 　　ｙ＝ｒ・ｓｉｎ（θ＋π/６） で与えられるので、求める軌跡の方程式は、 　　Ｃ’ ： ｘ2＋ｙ2＝３ｒ2

　ここで、曲線Ｃが囲む図形の面積は、４πｒ² で、曲線Ｃ’が囲む図形の面積は、３πｒ² な

ので、曲線ＣとＣ’で囲まれる図形の面積は、　４πｒ²−３πｒ²＝πｒ²　となる。

　ホルディッチの定理によれば、この曲線ＣとＣ’で囲まれる図形の面積は、上記では、

ｐ＝ｑ＝ｒ　の場合なので、　π・ｒ・ｒ＝πｒ²　で与えられることを意味する。

（注意）　上記は特別な場合で、求める軌跡Ｃ’は、原点中心で半径がＯＭ（＝ｒ）の円と
　　　　いうことは、上記のように計算しなくても自明だろう。

　自明ではない場合についても調べてみよう。

例　原点中心で半径が ２ｒ の円Ｃ ： ｘ²＋ｙ²＝４ｒ² において、長さ ２ｒ の弦を考える。弦ＡＢ
　　を ３：１ に内分する点Ｐの軌跡Ｃ’の方程式を求めてみよう。

　Ａ（２ｒ・ｃｏｓθ，２ｒ・ｓｉｎθ）、Ｂ（２ｒ・ｃｏｓ（θ＋π/３），２ｒ・ｓｉｎ（θ＋π/３））　とおくと、弦ＡＢ

を ３：１ に内分する点Ｐ（ｘ，ｙ）の座標は、

　　ｘ＝（２ｒ・ｃｏｓθ＋３・２ｒ・ｃｏｓ（θ＋π/３））/４＝ｒ（ｃｏｓθ＋３ｃｏｓ（θ＋π/３））/２

　　ｙ＝（２ｒ・ｓｉｎθ＋３・２ｒ・ｓｉｎ（θ＋π/３））/４＝ｒ（ｓｉｎθ＋３ｓｉｎ（θ＋π/３））/２

で与えられるので、求める軌跡の方程式は、

　　４ｘ²＋４ｙ²＝ｒ²｛１０＋６（ｃｏｓ（θ＋π/３）ｃｏｓθ＋ｓｉｎ（θ＋π/３）ｓｉｎθ）｝
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　＝ｒ²｛１０＋６ｃｏｓπ/３｝＝１３ｒ²
より、　Ｃ’ ： ｘ²＋ｙ²＝１３ｒ²/４

　よって、 曲線ＣとＣ’で囲まれる図形の面積は、　４πｒ²−１３πｒ²/４＝３πｒ²/４　となる。

　ホルディッチの定理によれば、この曲線ＣとＣ’で囲まれる図形の面積は、上記では、

ｐ＝３ｒ/２、ｑ＝ｒ/２　の場合なので、π・３ｒ/２・ｒ/２＝３πｒ²/４　で与えられる。


（コメント）　上記では面積が計算しやすい場合について調べたが、この性質が一般の凸閉
　　　　　　曲線で常に成り立つとは驚きです！


　微分積分の教科書を参考にしながら、証明を考えてみた。

（証明）　滑らかな凸閉曲線をＣとし、弦ＡＢ（長さＬ＝ｐ＋ｑ）を ｐ ： ｑ に分ける点Ｈが描く曲

線をＣ’とする。分点Ｈの座標を（ｘ（ｔ），ｙ（ｔ））　（ただし、０≦ｔ≦２π）とする。

　また、弦ＡＢが ｘ 軸の正の向きとなす角をθ（ｔ）とする。θ（ｔ）は単調増加とする。

このとき、　Ａ（ｘ（ｔ）−ｐ・ｃｏｓθ（ｔ），ｙ（ｔ）−ｐ・ｓｉｎθ（ｔ））

　　　　　　　Ｂ（ｘ（ｔ）＋ｑ・ｃｏｓθ（ｔ），ｙ（ｔ）＋ｑ・ｓｉｎθ（ｔ））

　閉曲線Ｃ、Ｃ’で囲まれた図形の面積を、Ｓ、Ｓ’とする。

　閉曲線Ｃが、２つの弧

　　　ｘ＝Ｆ（ｙ）　（ａ≦ｙ≦ｂ）　、ｘ＝Ｇ（ｙ）　（ａ≦ｙ≦ｂ）　ただし、　Ｆ（ｙ）≧Ｇ（ｙ）

で描かれているとき、

　∫_Ｃ ｘｄｙ＝∫_ａ^b Ｆ（ｙ）ｄｙ＋∫_b^a Ｇ（ｙ）ｄｙ＝∫_ａ^b （Ｆ（ｙ）−Ｇ（ｙ））＝Ｓ

である。同様にして、　Ｓ’＝∫_Ｃ’ ｘｄｙ　である。

　よって、

Ｓ＝∫_Ｃ ｘｄｙ＝∫_Ｃ （ｘ（ｔ）−ｐ・ｃｏｓθ（ｔ））ｄ（ｙ（ｔ）−ｐ・ｓｉｎθ（ｔ））

　＝∫_Ｃ’ （ｘ（ｔ）ｄｙ（ｔ）−ｐ（ｃｏｓθ（ｔ）ｄｙ（ｔ）＋ｘ（ｔ）・ｄ（ｓｉｎθ（ｔ）））＋ｐ²・ｃｏｓθ（ｔ）ｄ（ｓｉｎθ（ｔ）））

　＝Ｓ’−ｐ∫_Ｃ’ （ｃｏｓθ（ｔ）ｄｙ（ｔ）＋ｘ（ｔ）・ｄ（ｓｉｎθ（ｔ）））＋πｐ²

　　ここで、　∫_Ｃ’ ｃｏｓθ（ｔ）ｄ（ｓｉｎθ（ｔ））＝∫₀^2π ｃｏｓ²θｄθ＝π　を用いた。

同様に、

Ｓ＝∫_Ｃ ｘｄｙ＝∫_Ｃ （ｘ（ｔ）＋ｑ・ｃｏｓθ（ｔ））ｄ（ｙ（ｔ）＋ｑ・ｓｉｎθ（ｔ））

　＝∫_Ｃ’ （ｘ（ｔ）ｄｙ（ｔ）＋ｑ（ｃｏｓθ（ｔ）ｄｙ（ｔ）＋ｘ（ｔ）・ｄ（ｓｉｎθ（ｔ）））＋ｑ²・ｃｏｓθ（ｔ）ｄ（ｓｉｎθ（ｔ）））

　＝Ｓ’＋ｑ∫_Ｃ’ （ｃｏｓθ（ｔ）ｄｙ（ｔ）＋ｘ（ｔ）・ｄ（ｓｉｎθ（ｔ）））＋πｑ²

　以上から、　ｑ（Ｓ−Ｓ’−πｐ²）＋ｐ（Ｓ−Ｓ’−πｑ²）＝０　により、

　　　（ｐ＋ｑ）（Ｓ−Ｓ’）＝πｐ²ｑ＋πｐｑ²＝πｐｑ（ｐ＋ｑ）

　　したがって、　Ｓ−Ｓ’＝πｐｑ　　が成り立つ。　　（証終）


（コメント）　厳密な証明とは言い難いが、何となくニュアンスが伝わるかな．．．。


　　以下、工事中！