楕円の面積　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　

楕円 　　　　　 で囲まれる部分の面積は、 　　　　　πａｂ で与えられる。

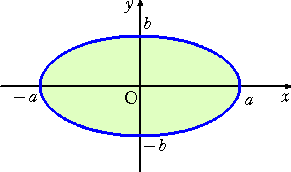　この証明は、通常、微分積分を用いて次のようになされる。

　求める面積を Ｓ とすると、

　　　　

　上式の定積分の計算は、置換積分を用いてもいいが、軽妙に「四分円の面積」から求め
る方が多数だろう。

　また、この楕円は、半径 ａ の円を ｙ 軸方向に ｂ/ａ 倍縮小して得られるという性質を用い
て、
　　　　πａ²×ｂ/ａ ＝ πａｂ

としても得られる。最も、この計算は、上記の定積分の計算が背景に存在する。

　何れにしても、楕円の面積の公式は、微分積分を根拠にしている。

　この問題について、関　孝和（1642？〜1708）は、著書「求積」で、微分積分によらない楕
円の面積の公式の証明を与えている。

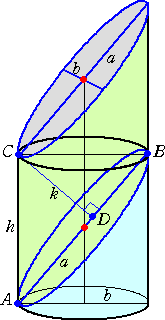左図は、半径 ｂ の円を底面とする円柱を、Ａ、Ｂ を通る平面 　で切断したときの切り口を表したものである。 　　このときの円柱の高さを、ｈ（＝ＡＣ）とすると、円柱の体積は、 　　　　　　　πｂ2ｈ 　である。 　　ＡＢ＝２ａ　とすれば、切り口は、長径が２ａ、短径が２ｂ　の楕 　円を表す。その面積を、Ｓ とおく。 　　切り口の下側の部分を、左図のように移動させても体積は同 　じである。 　　その立体図形の高さを、ｋ（＝ＣＤ）とすると、その体積は、 　　　　　　　Ｓｋ 　である。

　ここで、△ＡＢＣ ∽ △ＣＢＤ　なので、　ＡＢ ： ＡＣ ＝ ＣＢ ： ＣＤ が成り立つ。

　よって、　２ａ ： ｈ ＝ ２ｂ ： ｋ　より、　　ｋ ＝ ｂｈ/ａ　となるので、

　　　　　πｂ²ｈ ＝ Ｓｋ ＝ Ｓｂｈ/ａ

　したがって、　　Ｓ＝πａｂ　となる。

（コメント）　江戸時代に、微分積分を使わないで、上記のような計算で楕円の面積を計算し
　　　　　　た人が日本にいたということに、ただただ驚嘆するばかりである。

　また、正射影を使えば、次のようにも求められる。

　切り口の平面と底面のなす角を θ とすると、

　　　　　Ｓ・ｃｏｓθ＝πｂ²

である。　ここで、ｃｏｓθ＝ｂ/ａ　なので、　　Ｓ＝πａｂ　となる。

（コメント）　このような解答を見せられても、関　孝和の解法の美しさの前には、ただひれ伏
　　　　　　すのみである。


　Ｓ（Ｈ）さんからの出題です。（平成２３年５月２６日付け）

問題Ａ　　ｘ、ｙ、ｚ は、次の２つの条件を満たす実数とする。

　　　　　Ｓ₁ ： ｘｙ＋ｙｚ＋ｚｘ＝４４/１５　、　Ｓ₂ ： ｘ²＋ｙ²＋ｚ²＝５

　　　　　　　

（１）　このとき、ｘ の取り得る値の範囲 を求めよ。

（２）　上のＲ³に於ける２つの超曲面の Ｓ₁∩Ｓ₂ を、ｘｙ平面上に正射影すると、２つの楕円
　　　になる。このことを、主軸を求めて示し、図示せよ。

（３）　楕円の面積を求めよ。

問題Ｂ　　ｘ、ｙ、ｚ、ｗ は、次の２つの条件を満たす実数とする。

　　　　　Ｓ₁ ： ｘｙ＋ｘｚ＋ｘｗ＋ｙｚ＋ｙｗ＋ｚｗ＝７　、　Ｓ₂ ： ｘ²＋ｙ²＋ｚ²＋ｗ²＝９

（１）　このとき、ｘ の取り得る値の範囲 を求めよ。

（２）　上のＲ⁴に於ける２つの超曲面の Ｓ₁∩Ｓ₂ を、ｘｙｚ空面上に正射影すると、２つの楕円
　　　面になる。このことを、主軸を求めて示し、図示せよ。

（３）　楕円体の体積を求めよ。



　　　　以下、工事中